СОДЕРЖАНИЕ

Содержание…………………………………………………………………..2

Тех. Задание ………………………………………………….........................3

Введение………………………………………………………………...........4

Глава 1. Расчёты…………….………………………………………..............5

Заключение…………………………………………………………………..24

Список использованных источников………………………………............25

Введение

В данной курсовой работе рассматривается принципиальная схема и возможности вычисления цепи, в которой происходят процессы коммутации. Помимо прочего, рассматриваются анализы переходных процессов, используется классический метод определения закона о изменениях во времени ток и напряжения и т.д. (далее по списку решения задач изложенных в главе расчётов). Целью курсовой работы является закрепление и углубление знаний по дисциплине, а также изучение и освоение методов анализа и расчета характеристик линейных электрических цепей на постоянном и переменном токе на примере электрических цепей второго порядка.

Пояснительная записка содержит расчеты переходных процессов различными методами, а именно классическим и операторным методами в цепях постоянного и переменного тока.

Графическая часть курсовой работы включает:

- графики переходных процессов;

- график изменения искомой величины во времени на постоянном токе;

- график изменения искомой величины во времени при синусоидальной ЭДС

Глава 1. Расчёты.

Дано:

Е, В = 200

L = 1 мГн

C = 20 мКф

R1 = 4 Ом

R2 = 4 Ом

R3 = 2 Ом

R4 = 4 Ом

i₃ = ?



Источник постоянной ЭДС

Расчетная схема:

Заменим последовательно соединенные сопротивления эквивалентными:

R12 = R1 + R2 = 4 + 4 = 8 Ом



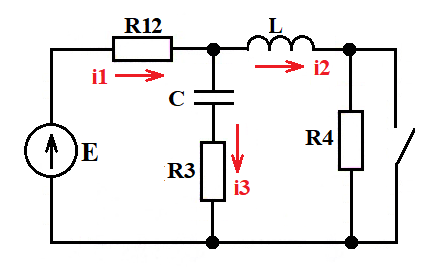
Найти: в соответствии с заданием.

Качественный анализ.

В схеме имеется два реактивных элемента поэтому эта цепь второго порядка и L и C задают в схеме независимые начальные условия (НУ) согласно законам коммутации. НУ условия не нулевые.

---

Цепь до коммутации и в установившемся режиме находится под действием постоянной ЭДС, поэтому конденсатор можно представить в виде разрыва, а катушку индуктивности в виде короткого замыкания, что и учитывается при расчете НУ.

Вид переходного процесса заранее определить невозможно - все зависит от корней характеристического уравнения.

1. Начальные условия

На постоянном токе в установившемся режиме конденсатор можно представить в виде разрыв цепи, а катушку индуктивности в виде короткого замыкания.

Р 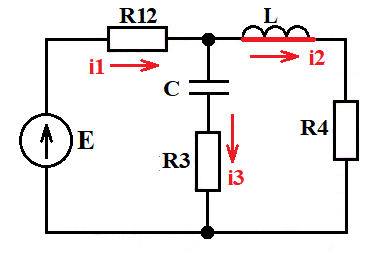асчет токов и напряжений до коммутации t(0-):

i1(0-) = i2(0-) = E/(R12 + R4) = 200/12 = 16,6667 A

i3(0-) = 0

uc(0-) = R4*i2(0-) = 4*16,6667 = 66,6668 В

Расчет токов и напряжений в установившемся режиме t(∞):

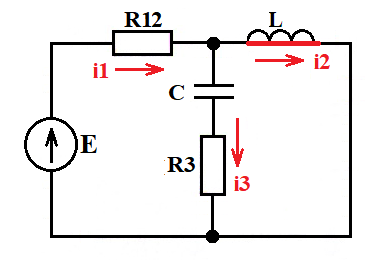
i1(∞) = i2(∞) = E/R12 = 200/8 = 25 A

i3(∞) = 0

uc(∞) = 0

Расчет токов и напряжений в момент коммутации t(0+):

По первому закону коммутации: i2(0+) = i2(0-) = 16,6667 А

По второму закону коммутации: uc(0+) = uc(0-) = 66,6668 В



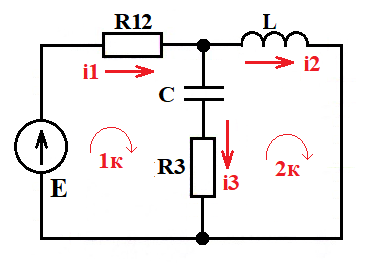
Дано:

E = 200 В

R12 = 8 Ом; R3 = 2 Ом; R4 = 4 Ом

L = 1 мГн; C = 20 мкФ

i2(0) = 16,6667 А

uc(0) = 66,6668 В

Согласно 1-му закону Кирхгофа для узлов:

1. 
   i1(0+) - i2(0+) - i3(0+) = 0
   

Согласно 2-му закону Кирхгофа для контуров:

Обход контуров по часовой стрелке.

2. 
   конт.1: R12*i1(0+) + R3*i3(0+) + uc(0+) = E
   
3. 
   конт.2: -R3*i3(0+) - uc(0+) + L*i2(0+)' = 0
   

Подставим значения:

4. 
   i1(0+) - i3(0+) = 16,6667
   
5. 
   8*i1(0+) + 2*i3(0+) = 133,3332
   
6. 
   -2*i3(0+) + 0,001*i2(0+)' = 66,6668
   

Из (4) получим:

i1(0+) = i3(0+) + 16,6667

Подставим в (5):

8*(i3(0+) + 16,6667) + 2*i3(0+) = 133,3332

8*i3(0+) + 133,3336 + 2*i3(0+) = 133,3332

i3(0+) = 0

uc(0+)' = i3(0+)/C = 0

Из (6) имеем:

0,001*i2(0+)' = 66,6668

i2(0+)' = 66,6668/0,001 = 66667 A/c

Продифференцируем (1, 2):

i1(0+)' - 66667 - i3(0+)' = 0

8*i1(0+)' + 2*i3(0+)' + i3(0+)/C = 0

8*i1(0+)' + 2*i3(0+)' = 0 → i1(0+)' = -2*i3(0+)'/8 = -0,25*i3(0+)

-0,25*i3(0+) - 66667 - i3(0+)' = 0

i3(0+)' = -66667/1,25 = -53333,6 A/c

2. Классический метод

Классический метод заключается в непосредственном решении дифференциальных уравнений I и II законов Кирхгофа, описывающих состояние цепи в переходном режиме.

Вид решения дифуравнения определяется корнями характеристического уравнения.

2. 1. Характеристическое уравнение.

---

Используем способ получения характеристического уравнения путем записи входного сопротивления zвх(p) относительно зажимов любой разомкнутой ветви, при этом источник тока удаляется, а ЭДС - закорачивается. Сопротивление определяем для момента времени t(0+), т.е. после коммутации.



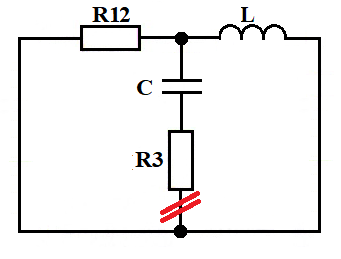
R12 = 8 Ом; R3 = 2 Ом

L = 1 мГн; C = 20 мкФ

z(p) = R3 + 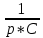+ 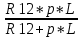= 2 + + =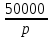

=

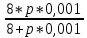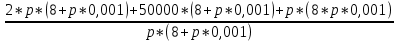
2*p*(8 + p*0,001) + 50000*(8 + p*0,001) + p²*0,008 =

= p*16 + p²*0,002 + 400000 + p*50 + p²*0,008 =

= p²*0,01 + p*66 + 400000

p²*0,01 + p*66 + 400000 = 0

p² + p*6600 + 40000000 = 0

Корни:

p1 = -3300 - 5395j

p2 = -3300 + 5395j

Корни комплексно-сопряженные, следовательно, решение для свободной должно иметь вид:

i1св(t) = А* 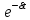**sin(ωo*t + ν)

δ = 3300; ωo = 5395

2. 2. Решение ищем в виде:

i3(t) = i3пр + i3св(t) = 0 + А* 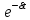**sin(ωo*t + ν) (7)

Постоянные интегрирования найдем из системы с учетом начальных условий:

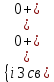(8)

Ранее получено:

i3(0+) = 0

i3(∞) = 0

i3св(0+) = i3(0+) - i3(∞) = 0

i3(0+)' = -53333,6 A/c

δ = 3300; ωo = 5395

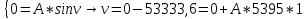
A = -53333,6/5395 = -9,89 А

В итоге получим:

i3(t) = -9,89* 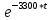*sin(5395*t)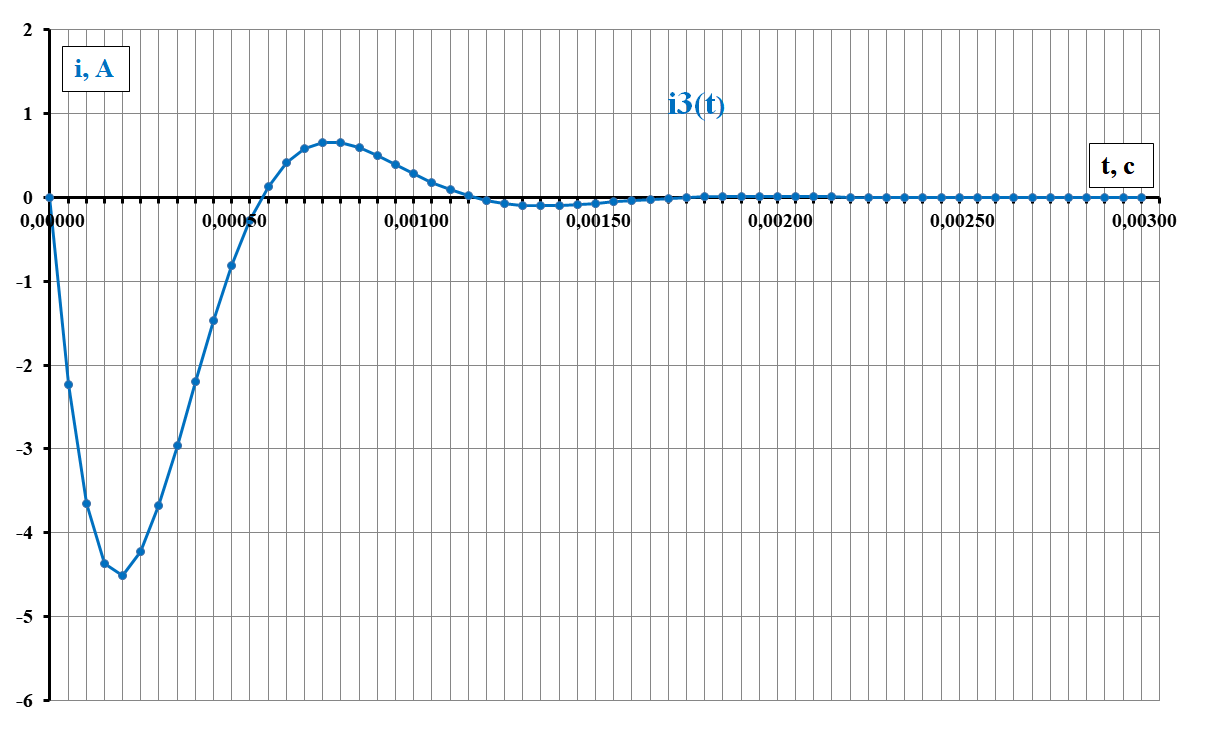



3. Операторный метод.

О 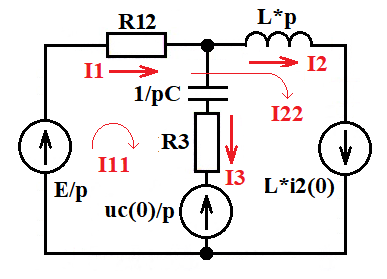ператорная схема замещения:

Дано:

E = 200 В

R12 = 8 Ом; R3 = 2 Ом

L = 1 мГн; C = 20 мкФ

i2(0) = 16,6667 А

uc(0) = 66,6668 В

Метод контурных токов.

Предполагается, что в каждом независимом контуре течет свой неизменный контурный ток. Уравнения составляют относительно контурных токов, после чего определяют токи ветвей через контурные токи.

---

При расчете МКТ полагают, что в каждом независимом контуре протекает неизменный (виртуальный) контурный ток. Если какая-либо ветвь относится лишь к одному конкретному контуру, то значение протекающего в нем реального тока будет равно контурному. В том случае, когда ветвь входит в состав сразу нескольких контуров, ток, протекающий в ней, будет представлять собой сумму, включающую в себя соответствующие контурные токи. В этом случае обязательно учитывается направление (знак) обхода контуров.

Обход контуров выберем по часовой стрелке.

3. 1. Контурные уравнения:

(R12 + R3 + 1/pC)*I11 + R12*I22 = E/p - uc(0)/p (1)

R12*I11 + (R12 + L*p)*I22 = E/p + L*i2(0) (2)

Подставим значения:

(10 + 50000/p)*I11 + 8*I22 = 133,3332/p

8*I11 + (8 + 0,001*p)*I22 = 200/p + 0,0166667

(p*10 + 50000)*I11 + p*8*I22 = 133,3332 (3)

p*8*I11 + p*(8 + 0,001*p)*I22 = 200 + p*0,0166667 (4)

Из (3) имеем:

I22 =

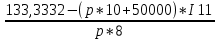
Подставим в (4):

p*8*I11 + p*(8 + 0,001*p)* 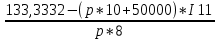= 200 + p*0,0166667

p*64*I11 + (8 + 0,001*p)*(133,3332 - (p*10 + 50000)*I11) = 1600 + p*0,1333

p*64*I11 + 133,3332*(8 + 0,001*p) - (8 + 0,001*p)*(p*10 + 50000)*I11 =

= 1600 + p*0,1333

[p*64 - (8 + 0,001*p)*(p*10 + 50000)]*I11 =

= 1600 + p*0,1333 - 133,3332*(8 + 0,001*p)

I11 = → =

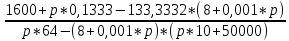Отдельно знаменатель:

p*64 - (8 + 0,001*p)*(p*10 + 50000) =

= p*64 - p*80 - 400000 - p²*0,01 - p*50 = - p²*0,01 - p*66 - 400000

p²*0,01 + p*66 + 400000 = 0

p² + p*6600 + 40000000 = 0

Корни:

p1 = -3300 - 5395j

p2 = -3300 + 5395j

Отдельно числитель:

1600 + p*0,1333 - 1066,6656 - 0,1333*p =

→ = =

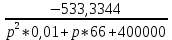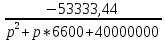
3. 2. Переход к оригиналу.

I1(p) = I3(p) =

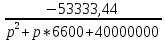
p1 = -3300 - 5395j

p2 = -3300 + 5395j

Согласно методу разложения на множители запишем:

F1 = -53333,44

F2 = p² + p*6600 + 40000000

F2' = 2*p + 6600

F2'(p1) = 2*(-3300 - 5395j) + 6600 = -10790j =

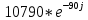
F2'(p1) = 2*(-3300 + 5395j) + 6600 = 10790j =

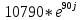
i3(t) = =

= - - = →

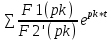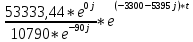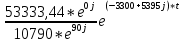= -4,94*

---

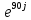
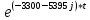* - 4,94* * =

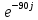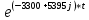Используем формулу Эйлера cosx = ( 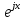+ 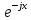)/2.

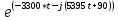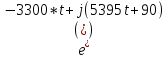→ = -9,88*( - /2 =

= -9,88* *cos(5395*t + 90) = -9,89* *sin(5395*t) А

В итоге получим:

i3(t) = -9,89* *sin(5395*t) А

Источник переменной ЭДС

e(t) = Em*sin(ω*t) = 120*sin(31416*t) В

ω = 2*f *π = 2*5000*π = 31415,9265 рад/с

Р 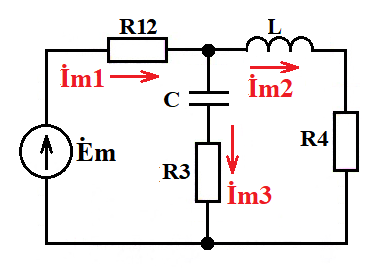асчетная схема:

Дано:

e(t) = 200*sin(31416*t) В; φe = 0

R12 = 8 Ом; R3 = 2 Ом; R4 = 4 Ом

L = 1 мГн; C = 20 мкФ

Найти: в соответствии с заданием.

Параметры элементов цепи:

xL = ω*L = 31415,9265*0,001 = 31,42 Ом

xc = 1/(ω*C) = 1000000/(31415,9265*20) = 1,59 Ом

Источник:

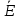m = Em 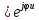= 200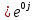 = 200 В

Комплексные сопротивления ветвей:

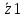= R12 = 8 = 8* 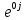, Ом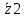

= R4 + jxL = 4 + 31,42j = 31,67* 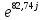, Ом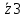

= R3 - jxc = 2 - 1,59j = 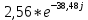, Ом

Эквивалентное комплексное сопротивление параллельных ветвей:

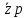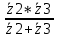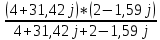= = = 2,2 - 1,5j = 2,66*

---

Смотрите также файлы

• Правила жаба Кто ехал на метле в сказке К. И. Чуковского Тараканище Животные 100 Правильный ответ На чем ехали медведи в сказке Тараканище Правильный ответ.pptx

• Расстройства теплового обмена. Лихорадка.docx

• Исследование содержания и особенностей открытия, принятия и отказа от наследства.docx

• 32. Жер Ай жйесі.docx

• раны Оыан білер р сзді (Абай) Шамшыра оушылар ылыми оамыны жмыс жасау баыттары.docx