Файл: История развития средств вычислительной техники ( Домеханический этап развития, использование простейших счётных приспособлений ).pdf
Добавлен: 29.02.2024
Просмотров: 64
Скачиваний: 0
В первые века второго тысячелетия вычисления на абаке во многом определяют характер средневековой математики. Крупнейшее руководство по математике, принадлежащее Леонардо Пизанскому, так и называлось — «Книга абака» («Liber abaci»). В этой работе, датированной 1202 г., JI. Пизанский констатировал наличие трех способов вычислений: счета на пальцах, подсчетов на абаке Герберта и выкладок на бумаге с помощью арабских цифр. Оба последних способа (счет на пальцах постепенно сходит на нет) продолжают развиваться и конкурировать друг с другом. Развитие абака в Западной Европе прежде всего заключается в замене абака Герберта счетом на линиях.
Из рассмотренных разновидностей абака счет на линиях напоминает счет в Китае на доске, расчерченной на квадраты. Русским аналогом счета на линиях был «счет костьми». В отличие от счета на линиях эти близкие ему разновидности абака явились предшественниками счетов (китайских и русских). Однако в Западной Европе, как отмечалось, дальнейшее развитие пошло по иному пути.
Для счета на линиях использовалась горизонтально разлинованная таблица и специальные металлические жетоны, которые назывались в Германии счетными пфеннигами, в других местах — фишками. В отличие от китайской клетчатой доски жетоны при счете на линиях выкладывались и на самых линиях и между ними. Разрядность повышалась снизу вверх, т. е. ближайшая к вычислителю линия предназначалась для единиц. Пять жетонов на любой линии были равны одному жетону, располагаемому непосредственно выше (между линиями), а два жетона между линиями равны одному жетону на проведенной линии. Таким образом, использовался двоично-пятеричный вариант десятичной системы счисления.
Сложение производилось простым выкладыванием слагаемых на линиях с последующим упорядочением по правилам разрядности. При выполнении вычитания вначале устанавливалось уменьшаемое, а затем, если это необходимо, некоторые жетоны заменялись более мелкими по значению. После этого снимались жетоны, соответствующие вычитаемому. Умножение производилось по схеме умножения многочлена на многочлен, а деление — по схеме, близкой к современной, но отвечающей специфике выкладывания жетонов на линиях.
Счетные таблицы два с лишним столетия были необходимой принадлежностью купца и чиновника, ученого и школяра. Счет на линиях вспоминают герои Шекспира - шут в «Зимней сказке» затрудняется решить задачу, не имея под рукой жетонов; Мольер в одной из своих последних постановок «Мнимого больного» заставил героя раскладывать на столе жетоны, чтобы проверить счета аптекаря; Лейбниц предпочитал счет на линиях арифметическим выкладкам на бумаге; в Германии, где этот способ удерживался до XVIII столетия, был известен экспромт, обычно приписываемый прусскому королю Фридриху II:
"Придворные - точь-в-точь жетоны, все их значенье - в положенье. В фаворе значат миллионы, но лишь нули в пренебреженье."
Счёт на линиях был описан в России в XV в. в книге "Счетная мудрость" под названием "счет костьми" (вишневыми или сливовыми косточками). Этим и объясняется замена европейского термина "счет на линиях" русским "счетом костьми"[[10], с.14]. Но если в Европе счет на линиях постепенно был вытеснен письменными вычислениями на бумаге, то в России "счет костьми" не выдержал конкуренции в борьбе с уникальным и замечательным средством вычислений – русскими счетами. Десятичный строй счетов веское основание для того, чтобы признать временем возникновения этого прибора XVI век, когда десятичный принцип счисления был впервые применен в денежном деле России. В 30-е годы XVI века московское правительство, возглавляемое Еленой Глинской, матерью малолетнего Ивана Грозного, провело денежную реформу, объединив московскую и новгородскую денежные системы. Московская деньга, составлявшая в то время 1/100 московского рубля, и ее половина - полушка - стали половиной и четвертью новой основной монетной единицы, которая получила название «копейка». Благодаря введению копейки рубль стал делиться на 100 основных единиц. Название прибора изменилось в XVII столетии. В 1658 г. впервые упомянуты "счоты" среди «рухляди» Никонова келейного старца Сергия в «Переписной книге домной казны патриарха Никона. А в начале XVIII в. счеты уже приняли вид, существующий и поныне. В них осталось лишь одно счетное поле, на спицах которого размещалось либо 10, либо 4 косточки (спица с четырьмя четками – дань "полушке", денежной единице в 1/4 копейки)[[11], с.16]. Русские счеты широко использовались при начальном обучении арифметике в качестве учебного пособия. Благодаря известному французскому математику и механику
Ж. Понселе, который познакомился со счетами в Саратове, будучи военнопленным офицером наполеоновской армии, аналогичный прибор появился во французских школах, а затем и в некоторых других странах Европы.
Как вычислительный прибор абак был прекрасно приспособлен для выполнения операций сложения и вычитания. Хотя умножение и деление до распространения десятичной системы с арабскими цифрами тоже производились на абаке, это был далеко не самый удобный способ выполнения этих действий. Поэтому понятно то глубокое впечатление, которое произвело крупнейшее изобретение шотландского математика Джона Непера (1550 — 1617) — логарифмы. В письме к М. Местлину от декабря 1618 г. Иоганн Кеплер писал: «Некий шотландский барон, имя которого я не запомнил, выступил с блестящим достижением, в котором он каждую задачу на умножение и деление превращает в чистое сложение и вычитание...»[[12], с.210]. Действительно, с помощью логарифмических таблиц можно было сравнительно легко выполнять умножения и деления больших чисел. Недостатком была сама необходимость пользования таблицами. Частично этот недостаток был устранен последующим изобретением логарифмической линейки (именно частично, поскольку аналоговый прибор в отличие от цифрового рассчитан на получение приближенных численных результатов).
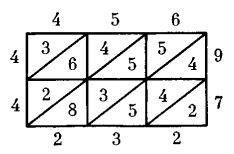
В основу изобретения Непера был положен широко известный в его время способ умножения решеткой. Этот способ был разработан в Индии и получил применение в ряде стран Востока. Способ умножения решеткой (или способ жалюзи) легко уяснить на примере. Пусть необходимо умножить 456 на 97. Рисуется прямоугольник, разбитый на шесть клеток. В клетках записывают произведения множимого и множителя, отделяя диагональю десятки от единиц: 4x9 = 3/6, 5x9 = 4/5 и т. д. Эти произведения суммируют по наклонным полоскам справа налево. Окончательный результат 456x97 = 44 232. Этот способ умножения Непер использовал, создавая свои счетные палочки. Впервые они были описаны в его работе «Две книги о счете с помощью палочек» («Rabdologiae seu numeration per virgulas libri duo»), часто называемой для краткости «Рабдология» («рабдос» по гречески означает «прут», «палочка»). Эта книга была издана в год смерти ее автора в Эдинбурге. Основное назначение палочек Непера — умножение больших чисел, а основной принцип работы — замена умножения сложением. Сами палочки (их девять) представляют собой таблицы умножения: 1, 2, 3-я палочки и т. д. представляют таблицы умножения 1, 2, 3 и т. д. на числа от 1 до 9. При этом каждое число в таблице умножения записано следующим образом: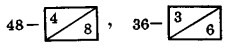 
и т.д. Умножение производится элементарно: 75 693 x 9 - выбираем палочки с номерами 7, 5, 6, 9, 3 располагаем их рядом с друг другом и прикладываем линейку к 9-й строке этих таблиц, где записано
, далее складываем по наклонным полоскам с права на лево и получаем итог: 681 237 [[13], с.6].
Сам инструмент выполнялся в виде прямоугольных брусков, разделенных на десять квадратов. Каждый квадрат, в свою очередь, кроме самого верхнего, делился по диагонали на две части, в каждой из которых в определенном порядке записывались числа (рис. 5)[[14]].
Рис. 5 Палочки Непера
Так же стоит обратить внимание на второе приложение к «Рабдологии» Непера. Это приложение называется «Арифметика» («Arithmetica localis») и содержит описание еще одного изобретения Непера — счётной доски для выполнения умножения, деления, возведения в квадрат и извлечения квадратного корня в двоичной системе счисления. Для записи чисел в двоичной системе Непер воспользовался следующим приемом; каждую степень числа 2 он обозначил отдельной буквой (а=2°=1, b=21=2, с =22=4 и т. д.). Из этих букв-цифр и формируется любое двоичное число, причем неперовская форма записи такого числа abc...n означает a+b+c...+n. Сами вычисления производятся с помощью доски, которая содержит 576 клеток (24X24), причем каждая клетка представляет число 2, возведенное в некоторую степень. Вычисления на счётной доске были громоздки, особенно при выполнении деления или извлечения квадратного корня, понятно, что доской Непера никто не пользовался в практических целях. Но современному человеку это устройство говорит о том, что Джон Непер был первым человеком, который более чем за триста лет до изобретения современных средств инструментальных вычислений, понял и оценил чисто арифметические достоинства двоичной системы счисления.
Ещё одно важное изобретение Непера - это изобритение логарифмов, о чем сообщалось в работе "Описание удивительной таблицы логарифмов", опубликованной в 1614 г. Логарифм – это показатель степени, в которую нужно возвести число, чтобы получить другое заданное число. Непер понял, что таким способом можно выразить любое число. Например,100 – это 102, а 23 – это 101,36173.
Более того, он обнаружил, что сумма логарифмов чисел а и b равна логарифму произведения этих чисел: ln a + ln b = ln (ab).
Благодаря этому свойству сложное действие умножения сводилось к простой операции сложения. Чтобы перемножить два больших числа, нужно лишь посмотреть их логарифмы в таблице, сложить найденные значения и отыскать число, соответствующее этой сумме, в обратной таблице, называемой таблицей
антилогарифмов. Основанием таблицы логарифмов Непера является иррациональное число, к которому неограниченно приближаются
числа вида (1 + 1/n)n при безграничном возрастании n. Это число называют неперовым числом и со времен Л. Эйлера обозначают буквой е: e =lim(1+ 1/n)n. Непер составил таблицы, взяв очень хорошее приближение числа е, а именно (1+1/107 )10^7.
Вскоре появляются и другие логарифмические таблицы. Они упростили вычисления, но все же эта операция оставалась достаточно трудоемкой и утомительной для тех, кому приходилось ею заниматься ежедневно. Поэтому вслед за изобретением логарифмов делаются попытки механизировать логарифмические
вычисления[[15], с.19].
Один из них и самый удачный это шкала Эдмунда Гюнтера (рис.6) профессора астрономии Грэшемского колледжа. На пластинке 600 мм в длину и 37 мм в ширину расположены 6 логарифмических шкал: чисел, синусов, тангенсов, синус-верзусов (была когда-то такая тригонометрическая функция sin vers a = 1 - cos а), синусов и тангенсов малых углов, синусов и тангенсов румбов, а также равномерные шкалы -«линия меридиана» и «линия равных частей». Эта шкала («шкала Гюнтера») представляла собой прямолинейный отрезок, на котором откладывались логарифмы чисел или тригонометрических величин.
Рис.6 Шкала Гюнтера
Циркули-измерители нужны были для сложения или вычитания отрезков вдоль линий шкалы, что в соответствии со свойствами логарифмов позволяло, находить произведение или частное. Логарифмическая шкала Гюнтера является прародительницей логарифмической линейки. Изобретателями первых логарифмических линеек независимо друг от друга являются Уильям Отред и Ричард Деламейн, которые в 1630-е гг. выпустили книги с описанием сових изобретений, это «Дополнение к использованию инструмента, называемого Кругами Пропорций» изданная в 1633г. Уильямом Форстером учеником Уильяма Отреда, где линейка состояла из двух логарифмических шкал. При употреблении они зажимались в левой руке вычислителя, и одна из них правой рукой смещалась относительно другой, неподвижной. И «Граммелогия, или Математическое кольцо» брошюра выпущенная в 1630г. Ричардом Деламейном, сдесь линейка состояла из вращающегося внутри кольца круга. В своей книге Деламейн привел несколько вариантов таких линеек, содержащих до 13 шкал. В специальном углублении Деламейн расположил плоский указатель, который мог перемещаться вдоль радиуса, облегчая использование вычислительного инструмента. В другой конструкции кольцо вращалось между неподвижным кругом и наружным кольцом. В 1654 г. англичанин Роберт Биссакер предложил конструкцию прямоугольной логарифмической линейки, сохранившуюся в принципе до нашего времени. Его линейка состояла из трех самшитовых планок длиной около 60 см: две внешние удерживались вместе медной оправкой, а третья (движок) свободно скользила между ними. Каждой шкале на неподвижных планках соответствовала такая же на движке. Шкалы имелись на обеих сторонах линейки. Немногим известно, что идея «бегунка» - неотъемлемого элемента современной линейки - была высказана Ньютоном. Но физически - как элемент логарифмической линейки - «бегунок» появился лишь спустя сто лет, когда Джон Робертсон, преподаватель Королевской математической школы предложил собственную линейку, предназначенную для навигационных расчетов. На одной ее стороне помещались равномерные, а на другой - логарифмические шкалы. Вдоль этой стороны двигался «индекс» - тонкая медная пластинка, с помощью которой можно было считывать соответствующие друг другу числа на различных шкалах линейки[[16], с.25].
В 1850 году Амедей Маннхейм, 19-летний французский офицер, служивший в
крепости Метц, предложил прямоугольную логарифмическую линейку, которая стала наиболее популярной среди инструментов подобного рода. Свой инструмент Маннхейм описал в брошюре «Модифицированная вычислительная линейка», изданной в 1851 году. В течение последующих 20 - 30 лет его линейки выпускались во Франции, а затем стали изготовляться фирмами Англии,
Германии, США. Расположение шкал на линейке Маннхейма близко к современному. Кроме того, ему удалось популяризировать применение «бегунка». Он показал, что «бегунок» можно использовать не только для считывания соответствующих чисел на далеко расположенных шкалах, но также и для сложных вычислений без записи промежуточных результатов. Линейка Маннхейма завоевала популярность во всем мире как портативный и удобный инструмент для ежедневных расчетов, обеспечивающий вычисления с точностью трех десятичных знаков.
Самый продолжительный из рассматриваемых этапов развития вычислительной техники - домеханический показывает, что основным двигателем усовершенствования приспособлений послужили такие факторы как развитие торговых отношений, инженерной мысли и науки (особенно это заметно в Эпоху Возрождения). Доминирующим приспособлением для вычислений на этом этапе стал абак и его дальнейшие усовершенствования приведшие к созданию, например, русских счетов и китайского суаньпаня. Эти приспособления полностью удовлетворяли потребности в финансовых расчётов торговцев и в большей своей массе создавались именно для них. Отсюда можно сделать вывод, что развитие торговых отношений их рост и увеличение стало началом прогресса вычислительной техники. Но это так же и объясняет почему этот этап был таким длительным, ведь для торговли, в большей своей массе, не требуются сложные вычисления, античная цивилизация потерпела крах и развитие образования как и фундаментальных наук остановилось. И только на закате Средневековья в Эпоху Возрождения в массах появился интерес к наукам, многим стало доступно образование, быть образованным становится престижно - это хорошо заметно т.к. именно в это время появляется масса выдающихся учёных. Один из них это Джон Непер создатель логарифма и счёта на полочках (палочки Непера). Всё это дало толчок к развитию инженерной мысли, положило начало развитию механики, что в свою очередь послужило толчком к более совершенному виду вычислительной техники и открыло механический этап в эволюции вычислений.