Файл: История развития средств вычислительной техники ( Домеханический этап развития, использование простейших счётных приспособлений ).pdf
Добавлен: 29.02.2024
Просмотров: 66
Скачиваний: 0
ГЛАВА 2. Механический этап развития
Под механическим вычислительным устройством понимается устройство, построенное на механических элементах и обеспечивающее автоматическую передачу из низшего разряда в высший.
Механический этап развития вычислительной техники можно начать вести с 1492 года, когда Леонардо да Винчи (1452-1519) разработал чертеж счетной машины и описал его в своих дневниках, ныне известных, как двухтомник «Codex Madrid». Похожие рисунки также были найдены и в рукописях«Codex Atlanticus». О использовании созданных Леонардо механизмов для счёта в его времена ничего не известно. Долгое время эти дневники пролежали в безызвестности в национальной Библиотеке Испании, пока 13-го февраля 1967 года не были найдены Роберто Гуателли известным экспертом по Леонардо да Винчи.
Среди чертежей первого тома «Мадридского кодекса», почти полностью посвященного прикладной механике, ученые обнаружили эскиз 13-разрядного суммирующего устройства с десятизубцовыми кольцами. Основу счетной машины составляли стержни с двумя зубчатыми колесами, большое - с одной стороны и маленькое - с другой. Как видно из эскиза Леонардо да Винчи, эти стержни располагались так, чтобы маленькое колесо на одном стержне входило в сцепление с большим колесом на соседнем стержне. Таким образом десять оборотов первого стержня приводили к одному полному обороту второго стержня, а десять оборотов второго - к одному полному обороту третьего стержня и так далее. Вся система состояла из тринадцати стержней и приводилась в движение набором грузов (рис.7)[[17]].
Рис.7  В 1969 г. по чертежам Леонардо да Винчи американская фирма IBM по производству компьютеров в целях рекламы построила работоспособную машину. Специалисты воспроизвели машину в металле и убедились в полной состоятельности идеи ученого.
В 1969 г. по чертежам Леонардо да Винчи американская фирма IBM по производству компьютеров в целях рекламы построила работоспособную машину. Специалисты воспроизвели машину в металле и убедились в полной состоятельности идеи ученого.
Ещё одним забытым и не применявшимся изобретением является машина Вильгельма Шикарда профессора восточных языков в Тюбингенском университете с 1617г.. Единственное упоминание о механизме сохранилось в письме Вильгельма Шикарда к Иоганну Кеплеру от 25 февраля 1623г. в котором Шикард описывает проект счётного механизма (рис.8) и даёт ему название "счетные часы" [[18], с.26].
Суммирующее устройство содержало два ряда осей с посаженными на них шестернями с десятью зубцами. В верхнем ряду было шесть осей (по числу разрядов), несущих, кроме 10-зубых шестерней, однозубые колеса (пальцы), наборные диски (они размещались на корпусе машины) и цилиндрические барабаны с цифрами (эти цифры были видны в окошках на корпусе машины). Нижний ряд из пяти осей нес на каждой оси только 10-зубую шестерню. Эти шестерни были вспомогательными: промежуточными между пальцем на верхней оси и находящейся справа от пальца 10-зубой шестерни (расположенной на соседней верхней оси, представляющей более старший разряд). Палец служил для автоматической передачи десятков в следующий разряд (с его помощью после полного поворота шестерни низшего разряда верхняя поворачивалась на 360°). Сложение осуществлялось последовательным вводом слагаемых с помощью наборных дисков, а вычитание — последовательным вводом уменьшаемого и вычитаемого. Различие состояло в том, что при сложении и вычитании наборные диски вращали в разные стороны [[19], с.55].
Рис.8 Рисунок машины , сделанный Шикардом
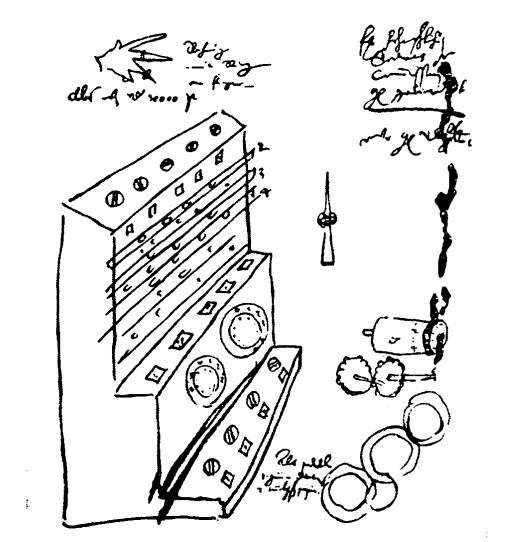
Вводимые в машину числа, а также результат сложения и вычитания можно было прочесть в окошках считывания.
Теоретически суммирующее устройство можно было использовать и для деления — путем последовательного вычитания делителя из делимого и записи количества таких вычитаний в устройстве для фиксирования промежуточных результатов. Для выполнения операции умножения использовалась идея умножения решеткой, использованная в палочках Непера. Третья часть машины использовалась для записи числа (обычно промежуточного результата при умножении) длиною не более 6 разрядов. Реализовано это было элементарно: поворачивая оси цилиндров с нанесенными на них цифрами от 0 до 9, мы устанавливаем любую совокупность этих цифр в шести окошках.
В связи с чумным мором и войнами изобретения Леонардо да Винчи и В. Шикарда небыли массово использованы, о них было известно единицам из современников изобретателей. Поэтому на дальнейшее развитие вычислительной техники данные механизмы не повлияли.
В 1640 г. попытку создать механическую вычислительную машину предпринял Блез Паскаль (1623 — 1662). В то время ему было 18 лет, но он был уже известен как математик, автор знаменитой теоремы Паскаля (в проективной геометрии), доказанной им в 16-летнем возрасте. Через несколько месяцев была изготовлена первая модель машины, однако она оказалась неработоспособной. По меркам XVII в. требования, предъявляемые Паскалем к точности механизмов, обеспечивающей их надежную работу, были высокими, но вполне выполнимыми. Лучшие мастера часового дела уже изготовляли в XVII в. весьма тонкие механизмы. Первая работающая модель машины была готова уже в 1642 году. Паскаля она не удовлетворила, и он сразу же начал конструировать новую модель. «Я не экономил,— писал он впоследствии, обращаясь к «другу-читателю»,—ни времени, ни труда, ни-средств, чтобы довести ее до состояния быть тебе полезной... Я имел терпение сделать до 50 различных моделей: одни деревянные, другие из слоновой кости, из эбенового дерева, из меди...»
Паскаль экспериментировал не только с материалом, но и с формой деталей машины: модели были сделаны — «одни из прямых стержней или пластинок, другие из кривых, иные с помощью цепей; одни с концентрическими зубчатыми колесами, другие — с эксцентриками; одни—движущиеся по прямой линии, другие— круговым образом; одни—в форме конусов, другие—в форме цилиндров...»
Наконец в 1645 году арифметическая машина, как назвал ее Паскаль, или Паскалево колесо, как называли ее те, кто был знаком с изобретением молодого ученого, была готова[[20], с.33]. Она представляла собой небольшой латунный ящик размером 36х13х8 см, содержащий внутри множество связанных между собой шестеренок и имеющий несколько наборных колесиков с делениями от 0 до 9, при помощи которых осуществлялось управление – ввод чисел для операций над ними и отображение результатов операций в окошках (рис.9). Каждое наборное колесико соответствовало одному разряду числа. Первые варианты устройства были пятиразрядными, впоследствии Паскаль создал шести- и даже восьмиразрядные варианты. Два младших разряда восьмиразрядной «Паскалины» были приспособлены для оперирования с денье и су, т.е. первый разряд был двадцатеричным, а второй двенадцатеричным, потому что в те времена французская монетная система была сложнее современной. В ливре было 12 денье, а в денье – 20 су. При выполнении обычных десятичных операций можно было отключать разряды, предназначенные для разменной монеты. Шести- и пятиразрядные версии машин могли работать только с десятичными цифрами[[21]].
Рис. 9 Модель "Паскалины"

В отверстиях располагались зубчатые колеса. Число зубьев каждого колеса равнялось числу делений шкалы соответствующего отверстия. Так, у крайнего правого колеса было 12 зубьев, у соседнего – 20, у остальных – по 10. Один из зубцов у каждой шестерни был немного удлинен и задевал соседнее колесо. Таким образом, полному повороту одного колеса соответствовал небольшой (1/20
или 1/10) поворот соседнего. Один поворот колеса соответствовал одной операции сложения. На боковых отверстиях барабана были нанесены цифры от 0 до 9, которые были видны в прямоугольных окнах крышки. В этих окнах
выводился результат арифметических операций. На этой машине можно было складывать[[22], с.29]. Механизм переноса десятков в машине Паскаля не позволяет обратного хода счетных колес (в отличие от машины Шиккарда). Паскаль заменяет операцию вычитания операцией сложения с дополнением к вычитаемому числу. Допустим, вместо того чтобы из 1 000 000 вычесть 33 333, мы прибавляем дополнение к этому числу. В машине Паскаля, рассчитанной, например, на работу с числами длиной 8 разрядов, эта операция будет выглядеть следующим образом: 01 000 000 + 99 966 666 = 00 966 666. Единица в старшем, девятом разряде (должно ведь быть 100 966 666) попросту исчезает: машина рассчитана на 8-разрядные числа. Теперь остается добавить единицу в самый младший разряд и получить искомый результат 966 667[[23], с.63]. Этот простой метод найденный Паскалем используется и в современных ЭВМ. Одну из первых удачных моделей «Паскалины» изобретатель подарил канцлеру Сегье, что помогло ему 22 мая 1649 года получить королевскую привилегию, подтверждавшую авторство изобретения и закрепляющую за Паскалем право на производство и продажу машины. После чего Паскаль печатает рекламное объявление в котором пишет как бы обращение к тем "кто будет иметь любознательность видеть арифметическую машину и пользоваться ею» и кому она облегчит работу, «часто утомлявшую ум при расчетах с помощью пера и жетона», тем самым он решил привлечь к покупке его машины людей занимающихся расчетами на бумаге и абаке. Однако развить производство и продажу машин не удалось, т.к. цена в 600 ливров была для большинства потенциальных покупателей слишком велика, да и функционал заключавшийся только в операциях сложения (операции вычитания, умножения и деления можно было выполнять только через сложение) был не удобен при постоянной работе. Поэтому практического применения в хозяйственной сфере машина Паскале не получила, в основном она использовалась как дорогая игрушка демонстрирующая могущество механики и человеческого разума. В 1653 г. в 30-летнем возрасте Паскаль навсегда оставляет занятия вычислительной техникой. По его мнению, конструкция вычислительной машины была доведена до необходимой степени совершенства, а практическое отсутствие спроса на нее делало излишним дальнейшее изготовление экземпляров. В отличии от машины В.Шикарда идеи использованные Паскалем в его суммирующей машине не ушли в забытье, а стали фундаментом в дальнейшем развитии вычислительной техники. Паскалина выставлялась в Люксембургском дворце на всеобще обозрение, её известность , создавала уверенность, что любые счетные операции можно механизировать. В XVII — XVIII вв. один изобретатель за другим предлагают новые варианты конструкций суммирующих устройств и арифмометров.
Первым в мире арифмометром - машиной, предназначенной для выполнения четырех действий арифметики (сложение, вычитание, умножение и деление), был арифмометр который изобрёл и создал в 1673г. немецкий философ, математик, физик Готфрид Вильгейм Лейбниц (1646–1716). Лейбниц начал работать над вычислительной машиной в молодости и продолжал работу до последних лет жизни. В возрасте 20 лет Лейбницу предложили должность профессора в Нюрнбергском университете (где он обучался с 15 лет). Он отклонил это предложение, предпочтя жизни ученого дипломатическую карьеру. Однако, пока он разъезжал в карете из одной европейской столицы в другую, его беспокойный ум терзали всевозможные вопросы из самых различных областей науки и философии - от этики до гидравлики и астрономии. В 1670г., Лейбниц делает первые описания (на латинском языке) «арифметического инструмента», находясь в Майнце. В 1672 г., находясь в Париже, Лейбниц познакомился с голландским математиком и астрономом Христианом Гюйгенсом. Видя, как много вычислений приходится делать астроному, Лейбниц решил изобрести механическое устройство, которое облегчило бы расчеты. «Поскольку это недостойно таких замечательных людей, - писал Лейбниц, - подобно рабам, терять время на вычислительную работу, которую можно было бы доверить кому угодно при использовании машины». В 1672г Лейбниц составил новое эскизное описание инструмента, а феврале 1673 г., продемонстрировал на заседании Лондонского королевского общества готовую модель. Как следует из протоколов заседания, Лейбниц, доложив о принципе работы и показав действие модели, отметил, что «прибор несовершенен, обещав его улучшить, как только вернется в Париж, где им нанят для этой цели мастер, которому он поручит изготовить для Королевского общества полный прибор». Сообщение Лейбница имело успех. В апреле 1673 г., уже после его отъезда из Лондона, он был избран членом Королевского общества [[24], с.66]. В 1674 – 1676 годах Лейбниц провел большую работу по улучшению изобретения и привез в Лондон новый вариант машины. Это была малоразрядная модель счетной машины, не пригодная для практического применения. И только в 1694 году Лейбниц сконструировал 12 разрядную модель, которую можно было назвать арифмометром. Впоследствии арифмометр несколько раз дорабатывался. Последний вариант был создан в 1710 году. По образцу двенадцатиразрядной счетной машины Лейбница в 1708 году профессор Вагнер и мастер Левин создали шестнадцатиразрядную счетную машину. Интересно, что один из первых экземпляров «арифметического инструмента» Лейбниц намеревался подарить Петру I, но машина оказалась неисправной, а механик ученого не смог ее починить в короткий срок. Лейбница интересовал молодой царь далекой Московии, которого он считал выдающимся "реформатором. Петр встречался и переписывался с Лейбницем, обсуждал с ним проект организации Академии наук в Петербурге и развертывания системы образования в России [[25], с.74].
Арифмометр представляет собой ящик около метра длинной, 30 сантиметров шириной и около 25 сантиметров высотой, если рассматривать сохранившуюся модель из музея в Ганновере [[26]]. Лейбниц пытался сначала лишь улучшить машину Паскаля, но понял, что для выполнения операций умножения и деления необходим совершенно новый принцип, который позволил бы: обойтись одной установкой множимого; вводить множимое в счетчик (то есть получать кратные и их суммы) одним и тем же движением приводной ручки.
Лейбниц блестяще разрешил эту задачу, предложив использовать цилиндр, на боковой поверхности которого параллельно образующей расположено 9 ступенек различной длины. Этот цилиндр .впоследствии получил название «ступенчатого валика». К ступенчатому валику крепится зубчатая рейка. Эта рейка входит в сцепление с десятизубым колесом №1, к которому прикреплялся циферблат с цифрами от 0 до 10. Поворотом этого циферблата задается значение соответствующего разряда множимого (рис. 10) [[27]].
Рис.10 Механизм ступенчатого валика.
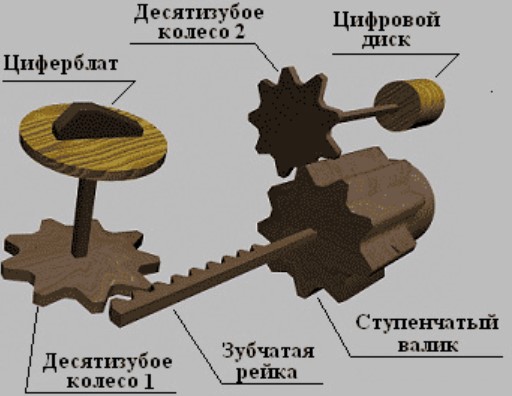
Например, если второй разряд множимого равнялся 5, то циферблат, отвечающий за установку этого разряда, поворачивался в положение 5. В результате десятизубое колесо № 1, с помощью зубчатой рейки, так перемещало ступенчатый валик, что при повороте на 360 градусов он входит в зацеплении с десятизубым колесом № 2 только пятью наиболее длинными ребрами. Соответственно, десятизубое колесо №2 поворачивалось на пять частей полного оборота, на столько же поворачивался и связанный с ним цифровой диск, отображающий результирующее значение выполненной операции.
При следующем обороте валика на цифровой диск снова перенесется пятерка. Если цифровой диск совершал полный оборот, то результат переполнения переносился на следующий разряд. Поворот ступенчатых валиков осуществлялся с помощью специальной ручки – главного приводного колеса. Таким образом, при выполнении операции умножения не требовалось многократно вводить множимое, а достаточно вести его один раз и повернуть ручку главного приводного колеса столько раз, на сколько необходимо произвести умножение. Однако, если множитель будет велик, то операция умножения займет длительное время. Для решения этой проблемы Лейбниц использовал сдвиг множимого, т.е. отдельно происходило умножение на единицы, десятки, сотни и так далее множителя.
Для возможности сдвига множимого устройство было разделено на две части - подвижную и неподвижную. В неподвижной части размещался основной счетчик и ступенчатые валики устройства ввода множимого. Установочная часть устройства ввода множимого, вспомогательный счетчик и, главное, приводное колесо располагаются на подвижной части. Для сдвига восьмиразрядного множимого использовалось вспомогательное приводное колесо (рис. 11) [[28]].
