Файл: Лабораторная работа 1 2 Построение компьютерной модели 2 Лабораторная работа 2 7.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 72
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рис. 1. Значения коэффициента лобового сопротивления для некоторых тел, поперечное сечение которых имеет указанную на рисунке форму
Взлет ракеты. Исследуем ситуацию, когда масса тела не является величиной постоянной. Запишем второй закон Ньютона в более общей математической форме.
Построим простейшую модель вертикального взлета ракеты, приняв следующие гипотезы:
-
масса ракеты уменьшается во время взлета по линейному закону:
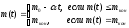 , (3)
, (3) гдеm0 начальная масса ракеты, заправленной топливом; mкон остаточная масса после полного выгорания топлива; расход топлива;
-
Сила тяги двигателя постоянна на всем участке взлета. -
плотность воздуха , входящая в коэффициент k2, убывает по мере подъема ракеты по закону = 0 . 10h, где h высота, 5,6 . 105 м1 .
Таким образом, модель будет описываться системой двух дифференциальных уравнений для функций v(t) и h(t):
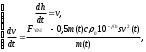 (4)
(4)Движение тела, брошенного под углом к горизонту. Дифференциальные уравнения модели получаются из второго закона Ньютона проецированием скорости и перемещения на горизонтальную и вертикальную оси координат:
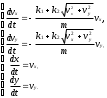
 (5)
(5)Здесь m масса тела; vx=vcos ,vy=vsin - величины проекций начальной скорости v на горизонтальную и вертикальную оси; угол начального наклона вектора скорости к горизонту; k1и k2 – коэффициенты, входящие в в формулу силы сопротивления.
Движение небесных тел. Рассмотрим модель движения космического тела (планеты, кометы, спутника) под действием силы всемирного тяготения в гравитационном поле, создаваемом телом с многократно большей массой.
Примем следующие предположения: «большое» тело находится в начале системы координат, другие тела на движение «малого» тела влияния не оказывают. Дифференциальные уравнения модели имеют вид
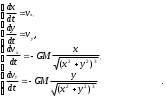 , (6)
, (6)где M- масса «большого» тела; x, y - координаты «малого» тела, движение которого изучается; vx, vy – величины проекций скорости «малого» тела на горизонтальную и вертикальную оси, G = 6,67. 1011 м3/кг с2 гравитационная постоянная .
Обезразмеривание. В задаче о движении небесных тел особенно неудобно работать с размерными величинами, измеряемыми миллиардами километров, секунд и т.д. В качестве величин для обезразмеривания удобно принять характерное расстояние от Земли до Солнца ρ = 1,496∙1011 м, (так называемая астрономическая единица), период круговой орбиты
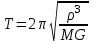 ,соответствующий этому расстоянию, скорость движения по ней
,соответствующий этому расстоянию, скорость движения по ней  , т.е. принять
, т.е. принять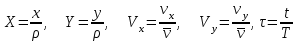
После обезразмеривания получаем
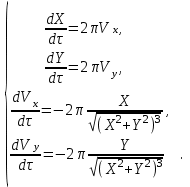 (7)
(7)В безразмерных переменных уравнения вообще не содержат параметров. Единственное, что отличает разные режимы движения друг от друга – это начальные условия.
Движение заряженных частиц. Рассмотрим модель движения заряженной частицы в кулоновском поле другой заряженной частицы, положение которой фиксировано.
В системе координат, начало которой привязано к «большому» телу, дифференциальные уравнения модели имеют вид
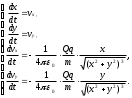 (8)
(8)Они получаются из второго закона Ньютона и закона Кулона.
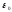 = 0,85 . 1012 ф/м электрическая постоянная. Знак “” в двух последних уравнениях соответствует разноименно заряженным частицам; в случае одноименных зарядов он меняется на “+”. Здесь qи Q соответственно заряды движущейся и закрепленной частиц; m масса движущейся частицы; xиy - координаты движущейся частицы;vx, vy- величины проекций скорости v движущейся частицы.на горизонтальную и вертикальную оси;
= 0,85 . 1012 ф/м электрическая постоянная. Знак “” в двух последних уравнениях соответствует разноименно заряженным частицам; в случае одноименных зарядов он меняется на “+”. Здесь qи Q соответственно заряды движущейся и закрепленной частиц; m масса движущейся частицы; xиy - координаты движущейся частицы;vx, vy- величины проекций скорости v движущейся частицы.на горизонтальную и вертикальную оси;Метод Эйлера решения обыкновенных дифференциальных уравнений.
Рассмотрим задачу Коши: Найти решение
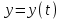 дифференциального уравнения
дифференциального уравнения 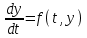 для
для 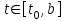 при начальном условии
при начальном условии 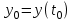 . Для численного решения уравнения проведем дискретизацию следующим простейшим способом: заменим непрерывные промежутки изменения tи yдискретными множествами значений, непрерывные функции –дискретными, производную – конечноразностным отношением. Получим :
. Для численного решения уравнения проведем дискретизацию следующим простейшим способом: заменим непрерывные промежутки изменения tи yдискретными множествами значений, непрерывные функции –дискретными, производную – конечноразностным отношением. Получим : 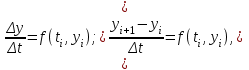 откуда получаем разностную схему Эйлера:
откуда получаем разностную схему Эйлера: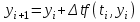 (9)
(9)Здесь отрезок
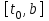 разбит на n равных частей длиной
разбит на n равных частей длиной 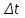 , так что
, так что 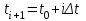 .
.Вопрос о выборе конкретного значения
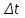 весьма непрост и определяется следующими соображениями. При компьютерном моделировании можно получить решение задачи о движении тела на некотором дискретном множестве значений t0, t0+ t, …, t0+(n-1)t. Чем больше величина t, тем меньшая точность в передаче значений непрерывных функций их дискретными представлениями. Однако, уменьшение шага t не всегда ведет к улучшению результатов моделирования. Одна из причин заключается в том, что чем меньше шаг, тем больше арифметических действий, ведущих к увеличению глобальной погрешности округления. Более эффективными при моделировании процессов, описываемых дифференциальными уравнениями, являются методы Эйлера-Коши или Рунге-Кутта более высокого порядка аппроксимации, чем метод Эйлера.
весьма непрост и определяется следующими соображениями. При компьютерном моделировании можно получить решение задачи о движении тела на некотором дискретном множестве значений t0, t0+ t, …, t0+(n-1)t. Чем больше величина t, тем меньшая точность в передаче значений непрерывных функций их дискретными представлениями. Однако, уменьшение шага t не всегда ведет к улучшению результатов моделирования. Одна из причин заключается в том, что чем меньше шаг, тем больше арифметических действий, ведущих к увеличению глобальной погрешности округления. Более эффективными при моделировании процессов, описываемых дифференциальными уравнениями, являются методы Эйлера-Коши или Рунге-Кутта более высокого порядка аппроксимации, чем метод Эйлера. Пример выполнения задания
Задача. Парашютист спрыгивает с высоты h0 и раскрывает парашют на высоте h1. Определить, будет ли скорость приземления безопасной.
Цель моделирования. Определить конечную скорость движения тела и сравнить ее с безопасной (10 м/с).
Формализация. Будем считать, что форма человека близка к сферической, форма парашюта – полусферической. Тело характеризуется массой m, радиусом (r- человека и r
1 – парашюта) и площадью поперечного сечения ( S и S1 соответственно). Среда характеризуется плотностью ρ и вязкостью μ. В ходе движения меняются время t, скорость v и высота h. Задача состоит в том, чтобы определить vкон в момент времени, когда h станет близкой к нулю.
Построение математической модели. Воспользуемся моделью (2):
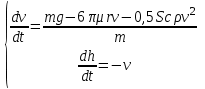
Выбор метода исследования. Применим для решения системы дифференциальных уравнений метод Эйлера:
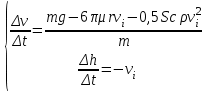 ;
; 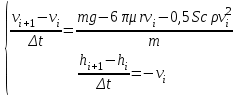 ;
; 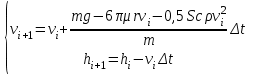
Построение компьютерной модели и ее проверка Выберем для моделирования среду табличного процессора Excel. Для проверки модели на адекватность рассмотрим движение без сопротивления среды (k1=0 и k2=0)
| Свободное падение тела | |||||||||
| Параметры движения | Параметры тела | Параметры среды | Коэффициенты | ||||||
| Время t0 | 0 | Масса m | 80 | Вязкость | 0,0182 | k1 | 0,000 | ||
| Скорость v0 | 0 | Радиус r | 0,3 | Плотность | 1,2 | k2 | 0,000 | ||
| Высота h0 | 1000 | Радиус r1 | 1,5 | | | | | ||
| Высота h1 | 800 | Площадь S | 0,053 | | | | | ||
| Шаг ∆t | 0,5 | Площадь S1 | 7,069 | | | | | ||
| | | Коэффициент с | 0,40 | | | | | ||
| | | Коэффициент с1 | 0,55 | | | | | ||
Рис. 2 Исходные данные задачи о свободном падении (сопротивление среды не учитывается)
Изменение скорости и высоты со временем
| t | v | h | ||
| 0 | 0 | 1000 | ||
| 0,5 | 4,9 | 1000,0 | ||
| 1 | 9,8 | 997,6 | ||
| 1,5 | 14,7 | 992,7 | ||
| 2 | 19,6 | 985,3 | ||
| 2,5 | 24,5 | 975,5 | ||
| 3 | 29,4 | 963,3 | ||
| 3,5 | 34,3 | 948,6 | ||
| 4 | 39,2 | 931,4 | ||
| 4,5 | 44,1 | 911,8 | ||
| 5 | 49,0 | 889,8 | ||
| 5,5 | 53,9 | 865,3 | ||
| 6 | 58,8 | 838,3 | ||
| t | v | h | ||
| 6,5 | 63,7 | 808,9 | ||
| 7 | 68,6 | 777,1 | ||
| 7,5 | 73,5 | 742,8 | ||
| 8 | 78,4 | 706,0 | ||
| 8,5 | 83,3 | 666,8 | ||
| 9 | 88,2 | 625,2 | ||
| 9,5 | 93,1 | 581,1 | ||
| 10 | 98,0 | 534,5 | ||
| 10,5 | 102,9 | 485,5 | ||
| 11 | 107,8 | 434,1 | ||
| 11,5 | 112,7 | 380,2 | ||
| 12 | 117,6 | 323,8 | ||
| 12,5 | 122,5 | 265,0 | | |

