Файл: Лабораторная работа 1 2 Построение компьютерной модели 2 Лабораторная работа 2 7.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 77
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
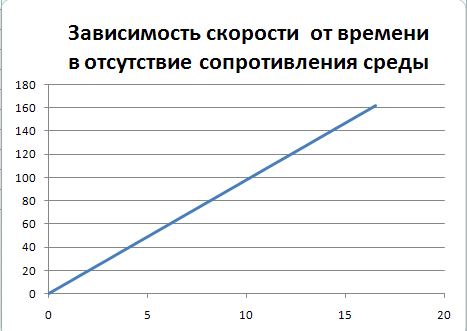
В отсутствие сопротивления среды скорость растет со временем по линейному закону, что соответствует аналитическому решению уравнений
Добавим силу сопротивления (
 и
и 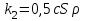 )
)| Свободное падение тела с учетом сопротивления | |||||||
| Параметры движения | Коэффициенты'>Параметры тела | Параметры среды | Коэффициенты (без парашюта) | ||||
| Время t0 | 0 | Масса m | 80 | Вязкость | 0,0182 | k1 | 0,045 |
| Скорость v0 | 0 | Радиус r | 0,3 | Плотность | 1,2 | k2 | 0,013 |
| Высота h0 | 1000 | Радиус r1 | 1,5 | | | Коэффициенты (с парашютом) | |
| Высота h1 | 800 | Площадь S | 0,053 | | | k1 | 0,515 |
| Шаг ∆t | 0,5 | Площадь S1 | 7,069 | | | k2 | 2,333 |
| | | Коэффициент с | 0,40 | | | | |
| | | Коэффициент с1 | 0,55 | | | | |
Изменение скорости и высоты со временем
| t | v | h |
| 0 | 0 | 1000 |
| 0,5 | 4,9 | 1000,0 |
| 1 | 9,8 | 997,6 |
| 1,5 | 14,7 | 992,7 |
| 2 | 19,6 | 985,3 |
| 2,5 | 24,4 | 975,5 |
| 3 | 29,3 | 963,3 |
| 3,5 | 34,1 | 948,7 |
| 4 | 38,9 | 931,6 |
| 4,5 | 43,7 | 912,2 |
| 5 | 48,4 | 890,3 |
| 5,5 | 53,1 | 866,1 |
| 6 | 57,8 | 839,6 |
| 6,5 | 62,4 | 810,7 |
| 7 | 10,3 | 779,5 |
| 7,5 | 13,7 | 774,3 |
| 8 | 15,8 | 767,5 |
| t | v | h |
| 8,5 | 17,0 | 759,6 |
| 9 | 17,6 | 751,1 |
| 9,5 | 17,9 | 742,3 |
| 10 | 18,1 | 733,3 |
| 10,5 | 18,2 | 724,3 |
| 11 | 18,2 | 715,2 |
| 11,5 | 18,2 | 706,1 |
| 12 | 18,2 | 697,0 |
| 12,5 | 18,2 | 687,9 |
| 13 | 18,2 | 678,8 |
| 13,5 | 18,2 | 669,7 |
| 14 | 18,2 | 660,6 |
| 14,5 | 18,2 | 651,5 |
| 15 | 18,2 | 642,3 |
| 15,5 | 18,2 | 633,2 |
| 16 | 18,2 | 624,1 |
| 16,5 | 18,2 | 615,0 |
В
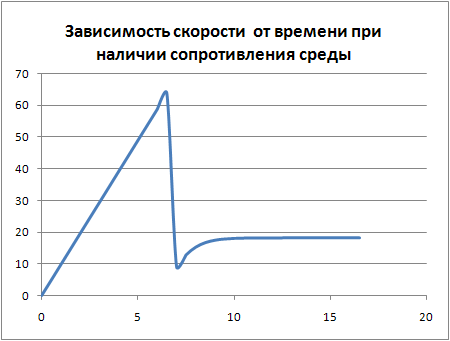 ывод. Если при падении с высоты 1000 м раскрыть парашют на высоте 800 метров,
ывод. Если при падении с высоты 1000 м раскрыть парашют на высоте 800 метров, то скорость падения 18,2 м/с значительно превысит безопасную
Использование модели
Данная модель позволяет решать не только описательные, но и оптимизационные задачи, например:
-
Найти оптимальную с точки зрения безопасности высоту раскрытия парашюта; -
Найти оптимальные размеры парашюта; -
Найти максимальную высоту, с которой можно спрыгнуть без парашюта и не пострадать и т.д.
Задание к лабораторной работе
-
Определить цель моделирования -
Провести формализацию задачи: сделать предположения, определить состав параметров, характеризующих объект, сформулировать задачу математически. -
Построить математическую модель (определить состав набора входных и выходных параметров, их конкретные числовые значения, записать уравнения).
-
Выбрать метод решения уравнений (в данном случае –один из численных методов). Записать решение уравнений в виде рекуррентных вычислительных схем. -
Определить значения параметров модели, начальные значения меняющихся в ходе движения величин, условия окончания вычислительных циклов. -
Построить компьютерную модель физического процесса в среде табличного процессора.
-
Произвести проверку модели на адекватность.
-
Выполнить конкретное задание из своего варианта работы.
-
Качественно проанализировать результаты моделирования.
Варианты заданий
Вариант 1.
Парашютист прыгает с некоторой высоты и летит, не открывая парашюта; на какой высоте (или через какое время) ему следует открыть парашют, чтобы иметь к моменту приземления безопасную скорость (не большую 10 м/с)?
Вариант 2.
Промоделировать падения тела с заданными характеристиками (масса, форма) в различных вязких средах. Изучить влияние вязкости среды на характер движения. Скорость движения должна быть столь невелика, чтобы квадратичной составляющей силы сопротивления можно было пренебрегать.
Вариант 3.
Промоделировать падения тела с заданными характеристиками (масса, форма) в различных плотных средах. Изучить влияние плотности среды на характер движения. Скорость движения должна быть достаточно велика, чтобы линейной составляющей силы сопротивления можно было пренебрегать (на большей части пути).
Вариант 4.
Глубинная бомба, установленная на взрыв через заданное время, сбрасывается со стоящего неподвижно противолодочного корабля. Исследовать связь между глубиной, на которой произойдет взрыв, и формой корпуса (сферической, полусферической, каплевидной и т.д.).
Вариант 5.
Глубинная бомба, установленная на взрыв на заданной глубине, сбрасывается со стоящего неподвижно противолодочного корабля. Исследовать связь между временем достижения заданной глубины и формой корпуса (сферической, полусферической, каплевидной и т.д.).
Вариант 6.
Промоделировать полет ракеты.
Провести исследование соотношения входных параметров m0 и Fтяги, при которых ракета достигнет первой космической скорости 7,8 км/с?(и в соответствующий момент исчерпает горючее). Остальные входные параметры фиксировать произвольно. Порядки входных параметров: m0 ˜ 107 кг, mкон ˜ 105 кг, ˜ 105 кг/c, Fтяги ˜ 108 н.
Вариант 7.
Промоделировать полет тела, брошенного под углом к горизонту. Исследовать зависимость горизонтальной длины полета тела от одного из коэффициентов сопротивления среды, фиксировав все остальные параметры.
Вариант 8.
Найти траекторию полета кометы, залетевшей в Солнечную систему, у которой на расстоянии от Солнца 100 астрономических единиц (1 а.е. = 1,50.1011 м расстояние от Земли до Солнца) скорость v=10 км/с и направлена под углом = 30о к оси «комета-Солнце». Является ли эта траектория замкнутой? Если да, то сколько длится для нее период полета? Подобрать то значение угла , при котором траектория из незамкнутой превращается в замкнутую (скорость v фиксирована).
Вариант 9.
Проверить в компьютерном эксперименте выполнимость второго закона Кеплера, определяющего движение небесных тел по замкнутой траектории.
Вариант 10.
Проверить в компьютерном эксперименте выполнимость третьего закона Кеплера, определяющего движение небесных тел по замкнутой траектории.
Вариант 11.
Найти траекторию движения тела массой 1 г., несущего заряд величиной q=1.102 к, в поле заряда величиной Q = 5 .102 к. Начальное расстояние между зарядами 1 м, начальная скорость равна 1.101 м/с и направлена под углом 30о к оси, соединяющей заряды. Провести моделирование для случая зарядов одного знака.
Вариант 12.
Имеется неподвижная заряженная частица с зарядом Q и экран (см. рис.7.2). В точке А экрана находится мишень. При каких соотношениях величины начальной скорости v0 движущейся частицы (заряд q) и угла прицеливания она попадет в мишень? Расстояния обозначены на рисунке. Заряды частиц разных знаков.

