Файл: Практикум инвестиционный анализ Направление подготовки 38. 03. 02 Менеджмент Профиль подготовки Менеджмент организации.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 19
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Сибирский государственный университет геосистем и технологий»
(СГУГиТ)
Кафедра цифровой экономики и менеджмента
ПРАКТИКУМ
инвестиционный анализ
Направление подготовки
38.03.02 Менеджмент
Профиль подготовки
Менеджмент организации
Квалификация (степень) выпускника
Бакалавр
Студент: Кухтина М.А.
Группа Бмз31
Руководитель: Ткаченко А.О.
Новосибирск, 2022
КОМПЛЕКТ ЗАДАНИЙ ДЛЯ КОНТРОЛЬНЫХ РАБОТ
Часть I. Приведение денежных потоков инвестиционного проекта по оси времени
В различные моменты времени денежные потоки имеют разную ценность. Чтобы привести денежные потоки различных временных периодов к сопоставимому виду, используют методы наращения или дисконтирования.
Приведите денежные потоки различных периодов от инвестиционного проекта по оси времени:
-
приведите денежные потоки к их текущей стоимости с использование фактора дисконтирования; -
найдите будущую стоимость денежных потоков, используя коэффициент наращения.
Исходные данные для выполнения расчетов приведены в табл. 9 (вариант выбирается в соответствии со списком обучающихся в журнале преподавателя или зачетной ведомости).
Фактор дисконтирования (DF) позволяет определить текущую стоимость одной денежной единицы, которая должна быть получена через n-периодов при заданной ставке дисконтирования (DR).
Коэффициент наращения (F) позволяет определить будущую стоимость одной денежной единицы через n-периодов при заданной ставке дисконтирования (DR).
Результаты решения записываются в табл. 10.
Таблица 9
Исходные данные по вариантам для выполнения контрольной работы по теме
«Приведение денежных потоков инвестиционного проекта по оси времени»
| Номер варианта | 19 |
| Потоки доходов, тыс.руб.: - за первый год, - за второй год, -за третий год. | 810 890 840 |
Фактор дисконтирования (DF) позволяет определить текущую стоимость одной денежной единицы, которая должна быть получена через n -периодов при заданной ставке дисконтирования DR:
DF1= 1/ (1+0,17) 1= 0,85
DF2 = 1/ (1+0,17) 2= 1,7
DF3 = 1/ (1+0,17) 3= 2,63
Коэффициент наращения (F) позволяет определить будущую стоимость одной денежной единицы через n -периодов при заданной ставке дисконтирования DR:
F1 = (1+0,17)1=1,17
F2 = (1+0,17)2=2,34
F3 = (1+0,17)3=3,51
Таблица 10
Приведение денежных потоков по оси времени
| Показатель | 1 год | 2 год | 3 год |
| Потоки доходов (СFt), тыс. руб. | 810 | 890 | 840 |
| Коэффициент дисконтирования (DF) | 0,85 | 1,7 | 2,63 |
| Текущая стоимость денежных потоков тыс. руб. | 688,5 | 1513 | 2209,2 |
| Коэффициент наращения (F) | 1,17 | 2,34 | 3,51 |
| Будущая стоимость денежных потоков, тыс. руб. | 947,7 | 2082,6 | 2948,4 |
Вывод: Текущая стоимость денежных потоков, через коэффициент дисконтирования за первый год уменьшается, за второй и третий год увеличивается.
Будущая стоимость денежных потоков, через коэффициент наращивания за первый, второй и третий год увеличивается.
Задание 2. Сравнение проектов различной продолжительности
Для сравнения и отбора инвестиционных проектов с использованием динамических методов сохраняется одно из условий альтернативности: срок функционирования проектов должен быть одинаков. Если же временной горизонт проектов различается, то необходимо проводить сравнение инвестиционных проектов с использованием специальных методов.
На данный момент в практике финансового анализа рассматривается три основных метода сравнения инвестиционных проектов разной продолжительности:
-
метод цепного повтора; -
метод бесконечного цепного повтора; -
метод эквивалентного аннуитета.
Сравните два инвестиционных проекта А и В, данные по которым приведены в табл. 11 и определите, какой из рассмотренных инвестиционных проектов является наиболее эффективным.
Таблица 11
Исходные данные по вариантам для выполнения контрольной работы по теме «Сравнение проектов различной продолжительности»
| № варианта | Проекты | DR, % | Чистые денежные потоки (CF) по шагам, тыс.руб. | |||||
| 0 | 1 | 2 | 3 | 4 | 5 | |||
| 19 | А | 17 | -1 500 | 2 800 | 1 200 | -1 800 | 3 500 | 3 800 |
| В | 18 | -5 300 | 5 100 | 5 100 | -1 000 | 7 000 | - | |
Пример расчета выполняется без табличной формы в развернутом виде.
Расчеты по методу цепного повтора:
NOK (5;4) = 20
NPVA = -1500+ (2800/ (1+0,17)1) + (1200/1+0,17)2) + (-1800/1+0,17)3) + (3500/ (1+0,17)4) + (3800/ (1+0,17)5) = 2291,3
NPVВ = -5300 + (5100 /(1+0,18)1) + (5100/ (1+0,18)2) + (-1000 /(1+0,18)3) + (7000 /(1+0,18)4) = 4079,5
NPVAN = 2291,3 + (2291,3 / 1+0,17)5) + (2291,3 / 1+0,17)5х2) + (2291,3 / 1+0,17)5х3)= 2909,3
NPVBN = 4079,5 + (4079,5 / 1+0,18)4) + (4079,5 / 1+0,18)4х2) + (4079,5 / 1+0,18)4х3) + (4079,5 / 1+0,18)4х4) = 9829,41
Вывод: Метод цепного повтора показал, что более предпочтительным для компании является Проект Б, поскольку для него настоящая стоимость бесконечного эквивалентного аннуитета больше, чем для Проекта А
Расчеты по методу бесконечного цепного повтора:
NOK (5;4) = 20
NPVA = -1500+ (2800/ (1+0,17)1) + (1200/1+0,17)2) + (-1800/1+0,17)3) + (3500/ (1+0,17)4) + (3800/ (1+0,17)5) = 2291,3
NPVВ = -5300 + (5100 /(1+0,18)1) + (5100/ (1+0,18)2) + (-1000 /(1+0,18)3) + (7000 /(1+0,18)4) = 4079,5
NPVA = (5; ∞) = 2291,3 * (1+0,17)5 = 2589,16
(1+0,17)5-1
NPVВ = (4; ∞) = 4079,5 * (1+0,18)4 = 4732,22
(1+0,18)4-1
Вывод:Вывод: Метод бесконечного цепного повтора показал, что более предпочтительным для компании является Проект Б, поскольку для него настоящая стоимость бесконечного эквивалентного аннуитета больше, чем для Проекта А.
Расчеты по методу эквивалентного аннуитета:
| № варианта | Проекты | DR, % | Чистые денежные потоки (CF) по шагам, тыс.руб. | |||||
| 0 | 1 | 2 | 3 | 4 | 5 | |||
| 19 | А | 17 | -1 500 | 2 800 | 1 200 | -1 800 | 3 500 | 3 800 |
| В | 18 | -5 300 | 5 100 | 5 100 | -1 000 | 7 000 | - | |
NOK (5;4) = 20
NPVA = -1500+ (2800/ (1+0,17)1) + (1200/1+0,17)2) + (-1800/1+0,17)3) + (3500/ (1+0,17)4) + (3800/ (1+0,17)5) = 2291,3
NPVВ = -5300 + (5100 /(1+0,18)1) + (5100/ (1+0,18)2) + (-1000 /(1+0,18)3) + (7000 /(1+0,18)4) = 4079,5
А ПроектА = 2291,3*0,17 = 721,3
1-(1+0,17)- 5
А ПроектВ = 4079,5*0,18 = 1529,7
1-(1+0,18)- 4
PVA ∞ПроектА = 721.3 = 4242.9
0.17
PVA ∞ПроектB = 1529.7 = 8498.3
0.18
Вывод: Метод эквивалентного аннуитета показал, что более предпочтительным для компании является Проект Б, поскольку для него настоящая стоимость бесконечного эквивалентного аннуитета больше, чем для Проекта А
Часть II. Портфельные инвестиции
Задание 3. Портфельные инвестиции
Номер варианта определяется по одной последней цифре зачетной книжки.
Инвестор располагает информацией
, отражающей динамику курсов и выплаченных дивидендов по акциям двух ведущих эмитентов A и B за десять прошедших месяцев. Курс акций на начало каждого месяца и размер выплаченных в каждом месяце дивидендов приведены в таблице.
Таблица - Динамика курсов и выплаченных дивидендов по акциям (ВАРИАНТ 1)
| Месяц, | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Курс акций А | 27,00 | 25,81 | 20,04 | 17,02 | 18,99 | 26,69 | 12,05 | 10,47 | 12,03 | 10,53 |
| Дивиденды от А | 2,17 | 0,22 | 5,44 | 7,85 | 6,14 | 0,66 | 1,80 | 2,64 | 0,01 | 0,18 |
| Курс акций В | 43,00 | 42,96 | 28,66 | 18,57 | 19,98 | 26,94 | 29,53 | 22,49 | 21,24 | 20,81 |
| Дивиденды от В | 0,16 | 0,55 | 0,92 | 5,65 | 4,64 | 10,34 | 0,54 | 7,56 | 0,00 | 0,03 |
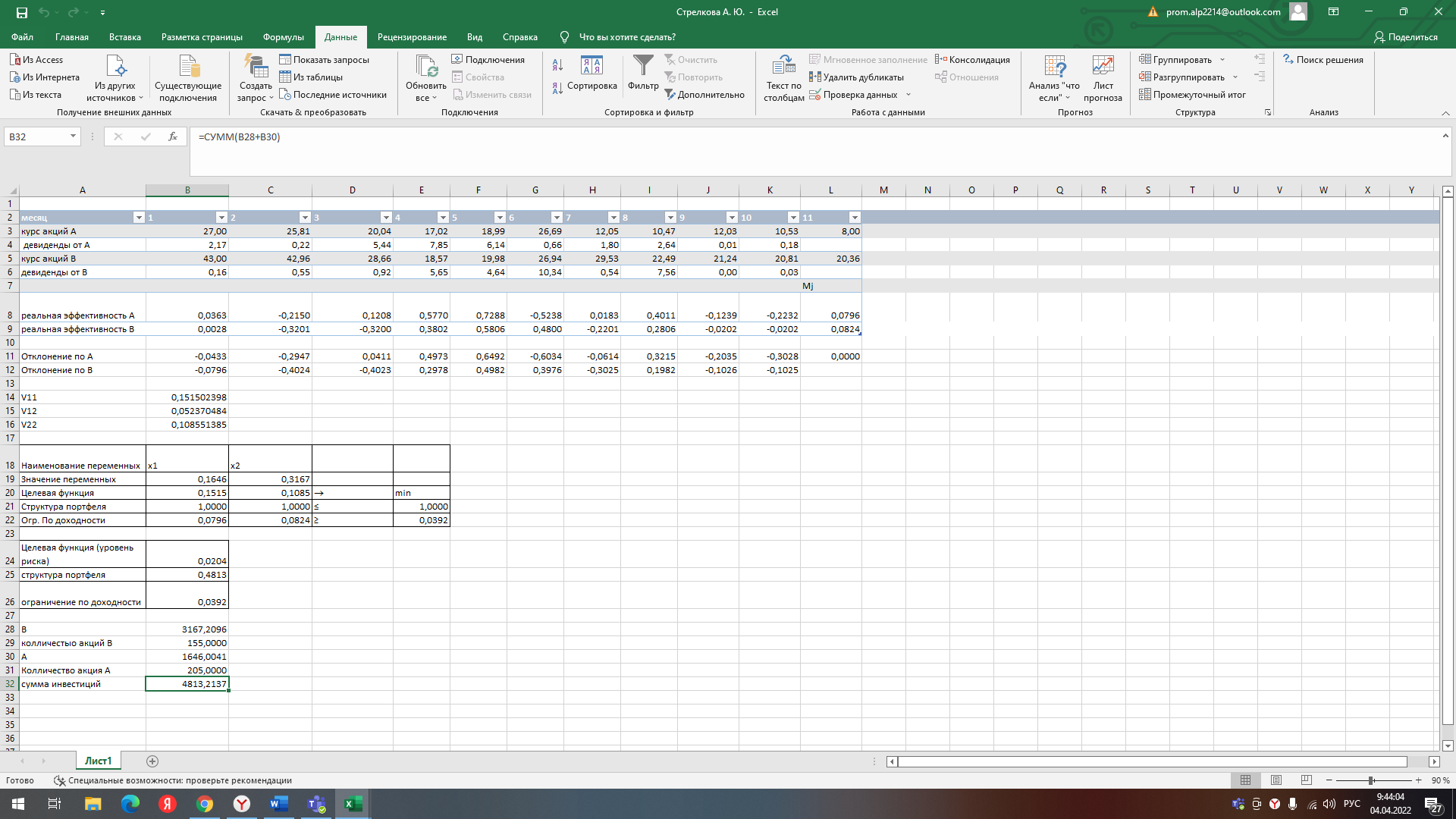
Курсы акций A и B на начало предстоящего одиннадцатого месяца составляют, соответственно, 8,00 руб. и 20,36 руб. В распоряжении инвестора имеется капитал в размере 10 тыс. руб., который он может использовать для покупки этих акций. Его интересует вопрос, акции какого эмитента и в каком количестве следует приобрести по их курсу на начало предстоящего месяца, чтобы с минимальным риском получить в этом месяце доход от покупки не менее 3,92 процента. Для ответа на интересующий инвестора вопрос необходимы следующие действия.
1. Построение экономико-математической модели расчета такой структуры инвестиций, которая при минимуме риска обеспечит желательный уровень доходности портфеля вложений.
2. Решение полученной задачи.