ФЕДЕРАЛЬНОЕ АГЕНСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА.

Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования «Петербургский государственный университет путей сообщения Императора Александра I»

(ФГБОУ ВО ПГУПС)


КУРСОВОЙ ПРОЕКТ

Дисциплина: Электрические машины

Специальность: 23.05.05 «Системы обеспечения движения поездов»

Специализация: «Автоматика и телемеханика на железнодорожном транспорте»

Форма обучения – ЗАОЧНАЯ

Защита: _____ _____________ ____________________

Оценка подпись, дата Ф.И.О

Группа: 07-006-11-АТя

Обучающийся: Смирнов И.В.

Преподаватель: Сульдин В.И

Ярославль

2023

Задача № 1.

Расчет магнитной цепи и параметров обмотки якоря машины постоянного тока.

В задаче требуется:

1. Произвести проверочный расчет магнитной цепи машины постоянного тока при холостом ходе, определить коэффициент насыщения магнитной цепи и, по результатам расчета, вычертить в масштабе эскиз магнитной цепи для одной пары полюсов.

2. Выбрать число коллекторных пластин, определить число витков в секции обмотки якоря и рассчитать шаги обмотки по элементарным пазам.

При выполнении работы принять, что сердечник якоря и сердечник полюсов набраны из листов электротехнической стали толщиной 0.5 мм., коэффициент заполнения сталью k_ст = 0.98, марка стали для якоря – 1211, марка стали для полюсов – 3411.

Станина машины постоянного тока, являющаяся также ярмом, по которому замыкается магнитный поток, выполняется из литой стали марки Ст.3. Пазы якоря открытые с параллельными стенками.

Высоту спинки якоря, толщину станины(ярма), ширину сердечника главного полюса и ширину зубца у основания необходимо рассчитать исходя из того, что в номинальном режиме значения магнитной индукции [Тл.] на этих участках магнитной цепи должны находиться в следующих пределах:

В_а = 1.3 –1.5; В_я =1.0–1.2; В_m =1.4 –1.6 ; В_z3 =1.9 –2.1.

Исходные денные:

D_a =220 мм. =0.220м.

L_a = 290 мм. = 0.29м.

P = 2

α_δ = 0.69

δ = 2,2 мм. = 0. 0022 м.

h_m = 73мм. = 0. 073м.

h_Z = 34мм. = 0,034м

σ = 1.1

Z = 39

U_н = 440

n_н= 1000об/ мин.

---

Обмотка якоря петлевая, машина работает в режиме двигателя.

1) Расчет магнитной цепи заключается в определении МДС обмотки возбуждения приходящейся на один полюс F_В = I_В ^.W_В и необходимой для создания заданного магнитного потока (I_В – ток возбуждения, W_В – число витков на полюс). Расчет МДС производится на основе закона полного тока, который может быть записан в виде:

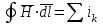(1)

где Н – вектор напряженности магнитного поля;

dl – вектор элемента длинны контура;

∑ i _k – алгебраическая сумма токов, охватываемых контуром.

При расчете магнитной цепи контур интегрирования выбирают совпадающим со средней магнитной линией. Магнитопровод разбивают на участки, напряженность магнитного поля на каждом из которых можно принять постоянной, а угол между векторами H и dl принять равным нулю.



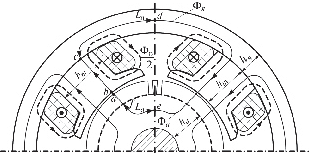
Рис. 1. Магнитная цепь машины постоянного тока

В результате интеграл в уравнении (1) можно заменить суммой, а в правой части уравнения будет МДС обмотки возбуждения приходящейся на один полюс:

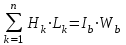(2)

Здесь H_k – напряженность магнитного поля на k – м участке магнитной цепи;

L_k – длина k – го участка магнитной цепи.

Магнитную цепь машины постоянного тока разбивают на 5 участков:

1) воздушный зазор;

2) зубцовый слой якоря;

3) сердечник главного полюса;

4) спинка якоря;

5) ярмо.

Так как магнитная цепь симметрична относительно оси, проходящей между двумя полюсами, то берется половина контура. Закон полного тока для данной магнитной цепи может быть записан в виде:

F_В = F_δ + F_z + F_m + F_a + F_я, (3)

где F_δ, F_Z, F_m, F_a, F_я - магнитные напряжения соответственно в воздушном зазоре, зубцовом слое, сердечниках полюсов, спинке якоря, ярме и равные произведению напряженности магнитного поля на участке магнитной цепи на длину этого участка.

---

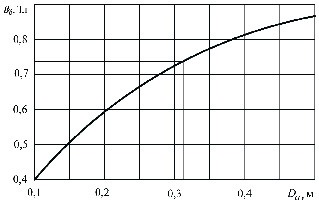
Расчет магнитной цепи начинают с выбора номинального значения магнитной индукции в воздушном зазоре В_δ по графику рис.2
_Рис. 2. Зависимость номинальной индукции в воздушном зазоре B_δ от заданного диаметра якоря D_a.

Принимаем:

D_a=0.220м ; B_δ = 0,65Тл.

Затем определяем значения магнитного потока на участках магнитной цепи: Ф_δ=В_δ ^. S_δ , Ф_а=Ф_δ/2 , Ф_m = σ ^. Ф_δ, Ф_я = Ф_m/2,

Где S_δ = l_δ ^. b_δ – площадь воздушного зазора под полюсом в м²;

σ – коэффициент магнитного рассеяния.

В нашем случае σ = 1.1

Расчетную ширину b_δ и длину l_δ воздушного зазора определяем по формулам:

b_δ = α_δ ^. τ ,

где τ = π ^.D_a / (2p)

lδ = 0,5 ^. (la + lm),

где lm = 0,29 – 0,005=0,285

В нашем случае:

D_a = 0,220м ,

p =2,

α_δ = 0,69,

l_a = 0,29м,

тогда τ = 3,14 ^. 0,220 / (2*2)=0,172м

b_δ = 0,69 ^. 0,172=0,118м;

l_δ = 0,5 ^. (0,29 + 0,285) = 0,869 м.

Отсюда площадь воздушного зазора под полюсом будет равна:

S_δ = 0,869 ^. 0,118 =0,102м²

Значения магнитного потока на участках будут равны:

Ф_δ = 0,65* 0,102= 0,066 Вб

Ф_а = 0,066/2 = 0,033 Вб

Ф_m = 1,1 ^. 0,066 = 0,072 Вб

Ф_Я = 0,072/2 = 0,036 Вб

Определим размеры, необходимые для вычерчивания эскиза магнитной цепи, а именно ширину полюса b_m, высоту спинки якоря h_a, высоту ярма h_Я:

b_m = Ф_m/ (B_m ^. l_mp),

где l_mp= l_m ^. k_ст =0,285*0,98=0,279

h_a = Ф_а / (В_а ^. l_ap),

где l_ap = l_a ^. k_ст=0,29*0,98=0,284

h_Я = Ф_Я / (B_Я ^. l_Я ) ,

где l_Я = l_m + 0,4 ^. D_a = 0,285+0,4*0,220=0,373 м

B_m = 1,5 Тл,

B_a = 1,4 Тл,

B_Я = 1,1 Тл,

В_z3 = 2 Тл,

k_ст = 0,98;

Следовательно:

b_m= 0,072/ (1,5 ^. 0,279 ) = 0,172м

h_a = 0,033 / ( 1,4 ^. 0,284) = 0,083 м

h_Я = 0,036 / ( 1,1 ^. 0,373) = 0,087м

При расчете магнитного напряжения в зубцах якоря необходимо учитывать, что, так как пазы якоря выполняют с параллельными стенками, то зубцы имеют разную ширину в верхней части и у основания и, соответственно разные значения магнитной индукции. Поэтому рассчитывают магнитную индукцию и напряженность магнитного поля в трех сечениях зубца. Для этого вначале определяют магнитный поток в зубце:

---

Ф_Z = B_δ ^. l_Z ^. t₁,

где l_Z = l_a ^. k_ст. – длина зубцов;

t₁ = π ^. D_a / Z – зубцовое деление.

D_a = 0,220 м , k_ст.= 0,98,

B_δ = 0,65Тл,

Z = 39, l_a = 0,29 м,

t₁= 3,14 ^. 0,220/39= 0,015 м ,

l_Z = 0,29 ^. 0,98= 0,284 м.

Ф_Z = 0,65 ^. 0,284 ^. 0,015= 0,0027Вб

Затем зададимся значением магнитной индукции в нижней части зубца B_Z3 = 2 Тл и найдем ширину этой части зубца :

b_Z3 = Ф_Z / B_Z3* l_Z = 0,0027/ (2 ^.0,284) = 0,004м

Находим ширину паза:

b_П=t₃–b_Z3=0,477–0,004=0,473м где t₃ = π ^.(D_a – 2 ^. h_Z) / Z = 3,14 ^. (0,220 – 2 ^. 0,034) / 39=0,477м

Находим ширину зубца и индукцию в верхнем сечении:

b_Z1 = t₁ – b_П = 0,015 – 0,473 = 0,0296м ;

B_Z1 = B_Z3 ^. b_Z3 / b_Z1 = 2 ^. 0,004 / 0,0296=0,27Тл

Индукция в средней части зубца будет:

B_Z2 = (B_Z1 + B_Z3) / 2 = (0,27 + 2 ) / 2 =1,135 Тл

Напряженности магнитного поля H_m, H_a, H_Я,H_Z1, H_Z2, H_Z3 находим с помощью кривых намагничивания сталей, по значениям индукции на соответствующих участках. Кривые намагничивания приведены в приложении в таблицах П1, П2, П3.

Принимаем:

B_m = 1,5 Тл → H_m = 2500 А/м

B_a = 1,4 Тл → H_a = 1580 А/м

B_Я = 1,1Тл → H_Я = 920 А/м

B_Z1 =0,27Тл → H_Z1 = 211А/м

B_Z2 = 1,135 Тл → H_Z2 = 1140 А/м

B_Z3 = 2 Тл → H_Z3 = 31000 А/м

Напряженность магнитного поля в воздушном зазоре равна:

H_δ = B_δ / μ₀ , где μ₀ = 1,26 ^. 10^-6 Гн/м – магнитная постоянная.

H_δ = 0,65/ 1,26 ^. 10^-6 = 515873 А/м

Определяем расчетную длину магнитной линии на каждом из участков :

L_δ = δ ^. k_δ , где k_δ = (10 ^. δ + t₁) / (10 ^. δ + b_Z1) – коэффициент воздушного зазора

k_δ =(10 ^.0,0022 + 0,015)/ (10 ^. 0,0022 + 0,0296) = 0,54

L_δ = 0,0022 ^. 0,54 = 0,0011м

L_Z = h_Z , L_m = h_m , L_a = π ^. ( D_a – h_a – 2 ^. h_Z) / (4 ^. p + 0,5 ^. h_a),

L_Z = 0,034м ,

L_m = 0,073 м,

L_a = 3,14 ^. (0,220 – 0,083 – 2 ^. 0,034)/ (4 ^. 2 + 0,5 ^. 0,083) = 0,65м

L_Я = π ^. (D_a + 2 ^. h_m + 2 ^. δ + h_Я) / (4 ^. p+0,5 ^. h_Я),

L_Я = 3,14 ^. (0,220+2 ^. 0,073+2 ^. 0,0022+0,087)/(4*2+0,5 ^. 0,087) =0,175м

---

Для получения МДС обмотки возбуждения в формулу (3) подставляем магнитные напряжения участков:

F_δ = H_δ ^. L_δ, F_Z= H_Zp ^. L_Z , F_m= H_m ^. L_m , F_a = H_a ^. L_a , F_Я= H_Я ^. L_Я

Расчетную напряженность магнитного поля в зубцах получают по формуле Симпсона:

H_Zp= (H_Z1+4 ^. H_Z2+H_Z3) / 6 =(211+4*1140 +31000)/6 =5961А/м

F_δ=515873 ^. 0,0011 =567,4 A ,

F_Z=5961* 0,034=202,6 A,

F_m=2500 ^. 0,073=182,5 A,

F_a=1580 ^. 0,65=1027 A,

F_Я=920 ^. 0,175=161 A

Для проверки степени насыщения магнитной системы машины вычисляют коэффициент насыщения:k_нас.=F_B/F_δ. Полученное значение должно находиться в пределах 1,1- 1,5 F_B= F_δ+F_Z+F_m+F_a+F_Я =567,4+202,6+182,5 +1027+161=2140,5 A, тогда коэффициент насыщения равен k_нас.=2140,5 /567,4=1,4, что соответствует требованиям.

2) Расчет параметров обмотки якоря рекомендуется начать с выбора числа элементарных пазов в реальном пазу u_П и определения числа коллекторных пластин:

K = u_П ^. Z, (4) , где Z – число пазов (зубцов) якоря.

Число коллекторных пластин выбирается из условия обеспечения нормальных потенциальных условий на коллекторе, чтобы среднее значение межламельного напряжения u_{k cp.} при холостом ходе не превышало 18 – 22 В.

K_min = 2 ^. p ^.U_Н/u_{k cp.} (5), где U_Н- нормальное напряжение.

U_Н=220В, приняв u_{k cp.}=22В получим из (5) минимальное число коллекторных пластин.

K_min= 2 ^. 2 ^. 440/22= 80

С другой стороны, максимальное число коллекторных пластин K_max определяется диаметром коллектора и минимально допустимым значением коллекторного деления.

t_{k min}= b_{k min}+Δ_{k из.} (6)

где b_{k min}- минимальная ширина коллекторных пластин;

Δ_{k из} – толщина межламельной изоляции.

Приняв D_k=0,7 ^. D_a=0,220 м , t_{k min}=0,005м , (b_{k min}= 0,004м, Δ_{k из}=0,001м), найдем:

K_max = 0,7^.π ^. D_a / t_{k min} (7)

K_max = 0,7 ^. 3,14 ^.0,220 / 0,005 = 96,7

Таким образом, целые числа u_k и К должны удовлетворять условиям:

K = u_k ^. Z и K_min ≤ K≤ K_max (8)

80≤ K ≤ 96,7

Определив по формулам (5) и (7) значения К_min и К_max выбираем числа u_П и К согласно условиям (8), где u_П = 1, 2, 3, … Принимаем u

---

Смотрите также файлы

• В. В. Волкова Субкультура и контркультура в современном обществе Данная статья.pdf

• В нынешней же системе образования главный акцент в обучении, воспитании и развитии делается на личность учащегося.doc

• Содержание введение 3 введение блокчейн распределенная база данных, которая хранит информацию обо всех транзакциях участников системы в виде цепочки блоков.doc

• Особенности инвестиционного рынка.docx

• Сценарий открытого занятия по пдд Безопасный мир.docx