ЛАБОРАТОРНАЯ РАБОТА № 4

НАДЕЖНОСТЬ НЕВОССТАНАВЛИВАЕМЫХ РЕЗЕРВИРОВАННЫХ СИСТЕМ
Цель работы: Определение количественных характеристик надежности невосстанавливаемых резервированных систем.

Задачи работы:

1. Изучить показатели надежности невосстанавливаемых резервированных систем.

2. Освоить методику расчетов показателей надежности невосстанавливаемых резервированных систем.
Сведения из теории
Резервированиемназывают метод повышения надежности системы за счет введения избыточности.

Под избыточностью при этом понимают дополнительные средства и возможности сверх минимально необходимых для выполнения системой заданных функций. Таким образом, задачей введения избыточности является обеспечение нормального функционирования системы после возникновения отказов в ее элементах.

По способу включения резервирование разделяется на постоянное и резервирование замещением. При постоянном резервировании резервные объекты подключены к нагрузке постоянно в течение всего времени работы и находятся в одинаковых с основными объектами условиях. При резервировании замещением замещают объекты основные (подключаются к нагрузке) после их отказа

Под кратностью резервирования "m" понимается отношение числа резервных объектов к числу основных. При резервировании с целой кратностью величина m есть целое число (например, если m = 2, то на один основной объект приходится два резервных). При резервировании дробной кратностью получается дробное несокращаемое число. Например, при m = 4/2, резервных объектов 4, основных 2, общее число объектов 6. Сокращать дробь нельзя, так как новое отношение будет отражать совсем другой физический смысл.
Общее резервирование с постоянно включенным резервом и с целой кратностью.
Структурная схема системы при общем резервировании с постоянно включенным резервом приведена на рис.4.1. Такая система откажет, если откажет основная цепь и все резервные.


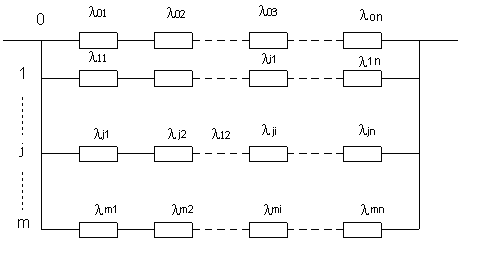
Рис. 4.1. Структурная схема системы с общим резервированием и постоянно включенным резервом (количество резервных цепей 0 <= j<=

---

m)
Вероятность безотказной работы основной и резервной цепей:
,
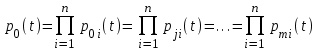где ­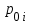 вероятность безотказной работы i-го элемента основной "0" цепи; 

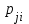­ вероятность безотказной работы i-го элемента j-й цепи.

Поскольку все одноименные элементы в каждой цепи имеют одинаковые параметры и находятся в одинаковых условиях, то надежность цепей в одно и то же время t одинакова:

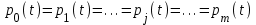
Вероятность отказа основной и резервной цепей:
,
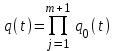где ­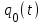 вероятность отказа основной цепи.

Поскольку все цепи идентичны и находятся в одинаковых условиях, то 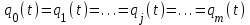, и тогда вероятность отказа системы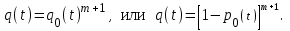

Вероятность безотказной работы системы с количеством цепей m+1
.
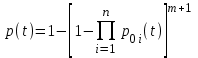В случае, когда 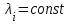, в каждой из цепей (экспоненциальное распределение времени до отказов элементов) вероятность безотказной работы, плотность распределения времени безотказной работы и интенсивность отказов системы с кратностью резервирования m определяются соотношениями:
,
,
.
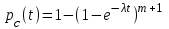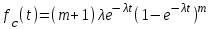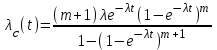Среднее время безотказной работы системы определяется выражением:

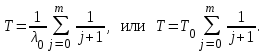
Общее резервирование замещением
Это метод повышения надежности системы за счет использования резервной цепи, находящейся в ненагруженном состоянии, которая автоматически включается при отказе основной цепи.

С
Для случая постоянных интенсивностей отказов элементов ( 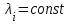) вероятность и среднее время безотказной работы системы вычисляются по формулам:

,

---

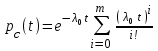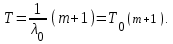
труктурная схема системы при общем резервировании с постоянно включенным резервом приведена на рис.4.2.



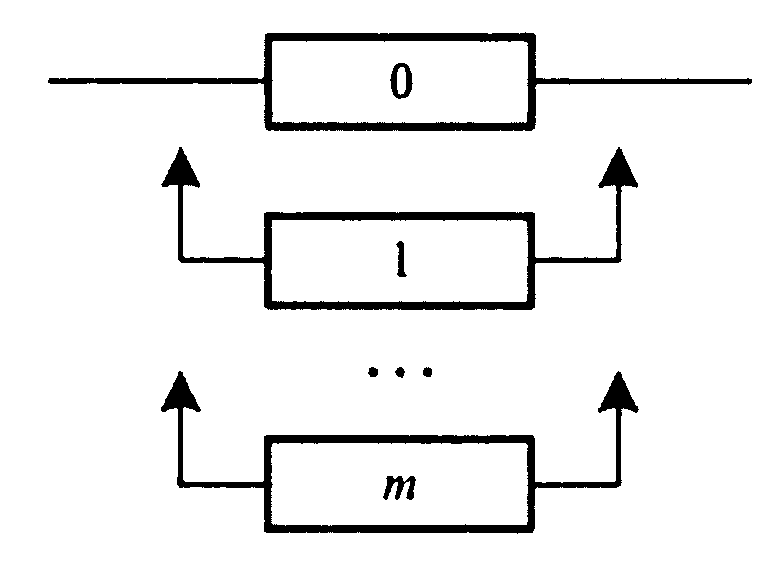
Рис.4.2. Структурная схема системы с общим резервированием замещением


Раздельное резервирование с постоянно включенным резервом и
Раздельное резервирование с постоянно включенным резервом и целой кратностью по всем элементам
Пусть исходная система состоит из n элементов, причем к каждому из них подключено m резервных элементов, как показано на рис. 4.3. Отказ этой системы может произойти при отказе любого блока. Совпадение работоспособных состояний n блоков системы гарантирует работоспособное состояние системы.


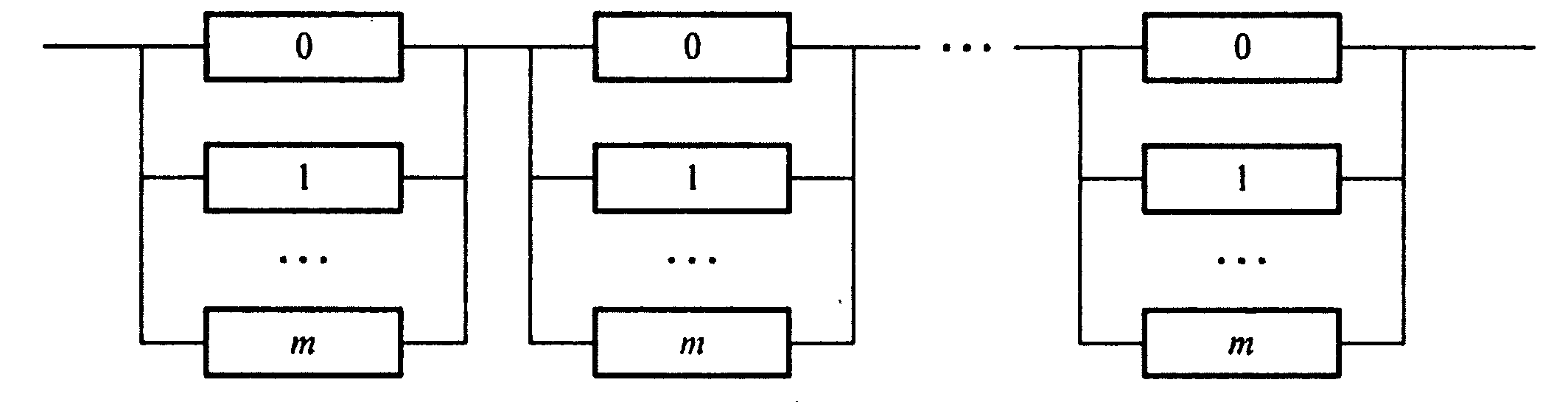
Рис.4.3. Структурная схема системы с раздельным резервированием с постоянно включенным резервом
Если известны вероятности безотказной работы каждого из блоков, то вероятность безотказной работы системы выражается формулой:


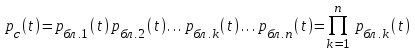
Интенсивность отказов основной цепи можно записать как:


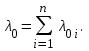
Если для элементов блока справедливо равенство 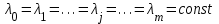, то вероятность безотказной работы блока элементов можно найти по формуле:
.
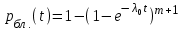Следовательно, вероятность безотказной работы системы при раздельном резервировании с целой кратностью определится по выражению произведения вероятностей безотказной работы блоков
,
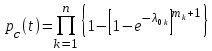где ­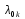 интенсивность отказов основного элемента  k-го блока; выражение в фигурных скобках - вероятность безотказной работы k -го блока.
Скользящее резервирование
Скользящее резервирование является частным случаем резервирования замещением, когда группа основных элементов аппаратуры резервируется одним или несколькими резервными элементами, каждый из которых может заменить любой отказавший основной элемент в данной группе (рис.4.4). Скользящее резервирование применяется при наличии в аппаратуре одинаковых узлов или блоков.

---

1 2 n



1

2
m
Рис. 4.4. Схема системы со скользящим резервированием:

1…n ­ основные элементы, 1…m ­ резервные элементы
Контрольные вопросы и задания
1. Дайте определению понятию «резервирование».

2. Какая задача решается при введении избыточности в техническую систему?

3. Что понимается под кратностью резервирования системы?

4. Перечислите основные виды резервирования. Дайте их определения.

5. Приведите структурную схему системы с постоянно включенным резервом.

6. Как определяется вероятность безотказной работы системы при общем резервировании замещением?

7. Приведите структурную схему системы с раздельным резервированием замещением.

8. Запишите формулы для вычисления безотказной работы системы при раздельном резервировании.

9. Проанализируйте особенности постоянного резервирования и резервирования замещением.

10. Чем отличается ненагруженный резерв от постоянного?

11. Какое резервирование систем называется скользящим?

12. В каких режимах могут работать резервные элементы в системах?
Варианты заданий к лабораторной работе
1. Система состоит из n блоков, вероятности безотказной работы каждого блока условно показаны на рис. 4.5. С целью повышения надежности системы произведено дублирование наименее надежных блоков такими же блоками. Найти вероятность безотказной работы системы.


Рис.4.5 Структурная схема надежности системы
2. Система состоит из 10 равнонадежных элементов, среднее время безотказной работы элемента составляет 1000 час. Предполагается, что справедлив экспоненциальный закон надежности для элементов системы и основная и резервная системы равнонадежны. Необходимо найти вероятность безотказной работы системы p_с(t), среднее время безотказной работы системы, а также частоту отказов f_c(t)и интенсивность отказов _с(t) в момент времени t= 50 час в следующих случаях:

а) система не резервированная,

б) дублированная система при включении резерва по способу замещения (ненагруженный резерв).

---

3. Интенсивность отказа одного элемента λ =0,0035 1/час. Требуется определить кратность резервирования системы (резерв замещением), построенной из этих элементов, которая обеспечивает среднее время безотказной работы, равное 800 час.

4. Вычислитель состоит из двух блоков, соединенных последовательно и характеризуется соответственно интенсивностями отказов₁120,5410^61/час и ₂185,6610^6 1/час. Выполнено пассивное резервирование второго блока. Требуется определить вероятность безотказной работы, среднее время безотказной работы, частоту отказов и интенсивность отказов вычислителя. Определитьp_с(t) при t час.

5. Электронный блок состоит из ста одинаковых модулей с интенсивностями отказов10^6 1/час и имеет в резерве три модуля, которые могут заменить любой из работающих. Определить вероятность безотказной работы блока за 1000 часов работы.

6. Найти показатели надежности p_с(t), _с(t), Tc резервированной системы (резерв замещением) кратности m=3, элементы которой имеют интенсивности отказа ₀0,041/час, ₁0,07 1/час,^,₂0,02  1/час,₃0,1  1/час. Решение получить в виде формул, таблиц и графиков.

7. Нерезервированная система управления состоит из n =4000 элемвнтов. Известна требуемая вероятность безотказной работы системы p_c(t) =0,9 при t=100 час. Необходимо рассчитать допустимую среднюю интенсивность отказов одного элемента, считая элементы равнонадежными, для того чтобы оценить достижение заданной вероятности безотказной работы при отсутствии профилактических осмотров в следующих случаях. а) резервирование отсутствует; б) применено раздельное (поэлементное) дублирование.

8. Поток отказов системы простейший. Система состоит из шести частей, отказ любой из них приводит к отказу всей системы. Определить, какая кратность постоянного общего резервирования системы обеспечивает ее безотказную работу в течение времени t часов (пусть t = 1 год ­ 8760 часов) с заданной вероятностью p_зад = 0.9), если средние наработки частей на отказ равны 5000, 3700, 4500, 8600, 9700, 12000 часов.

---

Смотрите также файлы

• Урок 107. Тв тема Примеры случайной изменчивости.docx

• Технологические угрозы сети Интернет.pdf

• 17 секретов word, которые облегчат вам работу.docx

• Пр 1 Целостный педагогический процесс единство обучения и воспитания Решение педагогической задачи.docx

• Тема Уникальное торговое предложение Задание 1.docx