Translated from Russian to Kazakh - www.onlinedoctranslator.com


Емтиханға қатысты 1сұрақтар
13. «Көпбурыштар. Геометриялық фигуралардың аудандары» тақырыбындағы оқу әдебиеті.
Мазмұны

1. 
   4,5-сыныптарда бұл тақырыпты оқыту қалай жүріп жатыр?
   
2. 
   аумақ ұғымын анықтауға бірыңғай көзқарас жоқ деген қорытындыға қандай анықтамаларды қолдануға болады?;
   
3. 
   бұл анықтамалар туралы не айтуға болады?
   
4. 
   8-сыныптың геометрия курсында аудан ұғымы қалай енгізіледі?
   
5. 
   8-сынып геометрия оқулығы (авторлары И.Бекбоев, Ә.Әбдиев, Ж.Қайдасов, Г.Хабарова);
   
6. 
   «Фигуралар квадраты» тақырыбын оқу курсына тағы қандай материалды қосуға болады?
   

Оқушылар фигуралардың аудандары туралы алғашқы түсініктерін 5-сыныпта алады, олар екі негізгі қасиетімен танысады:

• 
  тең фигуралардың аудандары тең болады;
  
• 
  Егер фигура бөліктерге бөлінсе, онда бүкіл фигураның ауданы осы бөліктердің аудандарының қосындысына тең болады.
  

4-сыныпта шаршының, тіктөртбұрыштың ауданы туралы түсінік беріледі, мұнда палитра арқылы фигураның ауданы анықталады: фигураны қамтитын бірлік квадраттардың саны есептеледі.

Оқушылар 8-сыныпта жазық фигуралардың аудандары туралы нақтырақ түсінік алады. Алайда оқу-әдістемелік әдебиеттерде облыс ұғымын анықтауға бірыңғай көзқарас жоқ:

• 
  фигураның ауданы - бұл фигура алып жатқан жазықтықтың бөлігі;
  
• 
  қарапайым көпбұрыштың ауданы - бұл көпбұрышпен шектелген жазықтық бөлігінің өлшемін анықтайтын сан;
  
• 
  тұйық фигураның ауданы - көпбұрыштың немесе басқа жазық жабық фигураның ішінде қоршалған жазықтық бөлігінің өлшемі.
  

1. 
   анықтамасы ыңғайсыз, өйткені оның астына аудан ұғымы және көпбұрыш ұғымы сәйкес келеді;
   
2. 
   әдістемелік тұрғыдан оқушыларға ең жақын және ең түсініктісін анықтау;
   
3. 
   анықтамада «құндылық» ұғымы қолданылады, сондықтан бұл анықтаманы бермес бұрын «құндылық» түсінігімен танысу керек.
   

8-сыныпта аудан ұғымы 5-сыныптағыдай, кесіндінің ұзындығы туралы түсінік беріледі. Көпбұрыштардың аудандарының формулалары аудандардың келесі қасиеттеріне негізделген:

- тең көпбұрыштардың аудандары тең болады;

- егер көпбұрыш бірнеше көпбұрыштан тұрса, онда оның ауданы

көпбұрыштар мүшелерінің аудандарының қосындысына тең:

---

8-сынып геометрия оқулығында (авторлары И.Бекбоев, Ә.Әбдиев, Ж.Қайдасов, Г.Хабарова) жазық фигураны өлшеудің мынадай негізгі қасиеттері берілген:

1. тең фигуралардың аудандары тең болады;

2. егер фигура қарапайым фигура болып табылатын бөліктерге бөлінсе, онда бұл фигураның ауданы осы бөліктердің аудандарының қосындысына тең болады (қарапайым фигура деп бөлуге болатын фигура жатады) үшбұрыштардың ақырлы саны);

3. қабырғасы өлшем бірлігіне тең шаршының ауданы бірге тең.

Ауданы бірдей фигуралардың анықтамасы берілген: аудандары бірдей фигуралар тең аудан деп аталады.

«Фигуралар ауданы» тақырыбын оқу барысында тарихи мәліметтерді қосу және бұл тақырыпты тәжірибеде қолдану пайдалы болады (мәліметтерді «Геометрия-8» оқулығынан алуға болады - авторлар И. Бекбоев, А. Әбдиев, Ж.Қайдасов, Г.Хабарова, сонымен қатар «Бастауыш сыныптағы математика негіздері» оқулығында – қазақ тілінде – авторлар Абдрахманов Қ.Қ., Ермекбаева А.Е.

он төрт.Болшек сандарды оқыту әдебиеті

Мазмұны

1. 
   Бөлшек сандармен таныстыру
   
2. 
   Бөлшек сандарды нөмірлеу
   
3. 
   Жай бөлшек ұғымымен таныстыру
   
4. 
   Жай бөлшектерге амалдар
   

Оқыту тәжірибесінде бөлшек сандарды оқытудың негізгі әдісі студенттердің өмірлік тәжірибесі мен біліміне негізделген түсіндірме сипаттамалар болып табылады. Түсіндірме сипаттамалар анықтамаларды, ұғымдарды алмастырмайды, тек оларды енгізудің орындылығын көрсетеді.Оқыту тәжірибесінде бөлшек сандарды оқытудың негізгі әдісі оқушылардың өмірлік тәжірибесі мен біліміне негізделген түсіндірме сипаттамалар болып табылады. Түсіндірме сипаттамалар анықтамаларды, ұғымдарды алмастырмайды, тек оларды енгізудің мақсаттылығын көрсетеді. Мектеп курсына бөлшек сандарды енгізу шамаларды дәлірек өлшеу қажеттілігімен, сандарды бөлумен байланысты. Осыған байланысты студенттерді адамның практикалық іс-әрекеті процесінде, атап айтқанда, өлшеу процесінде бөлшек сандардың пайда болуымен таныстырған жөн. Қысқаша тарихи дерек студенттерге бұл материалды жақсы меңгеруге көмектеседі.

Өлшеу, сондай-ақ санау барлық халықтарда ең көне заманнан бері орын алған; өлшеу баллмен тікелей байланысты болды. Өлшем бірліктерінің екі, үш немесе одан да көп бөліктерге бөлінуіне дәлірек өлшеу қажеттілігі себеп болды. Бұл кішірек өлшемдерге арнайы атаулар берілді және болашақта шамалар олармен біртекті осы кіші өлшем бірліктермен өлшенді. Алғашқы бетон фракциялары осылай пайда болды. Математика бойынша бағдарлама мен оқулыққа сәйкес бөлшек ұғымдарын қалыптастыру шаманы бірнеше тең бөліктерге бөлу кезінде үлесті алу мүмкіндігінен басталады.

---

Оқушыларға таныс заттарды қарбыз, қауын, бәліш, т.б. тең бөліктерге бөліп, бөліктердің бірін, үлестердің бірін таңдау ұсынылады. Оқушылар геометриялық материалды пайдалана отырып, бір сипаттағы жаттығуларды орындайды: кесіндіні, шеңберді, шаршыны тең бөліктерге, тең үлестерге бөлу және осындай бір бөлікті, бір үлесті алу. Бір бөлікті таңдаудан және бірнеше осындай бөліктерді алудан.

Оқушыларға заттың бір немесе бірнеше бөлігін өрнектеу үшін жаңа сандар, атап айтқанда бөлшектер қажет екендігі айтылады. Төменде жай бөлшекке мысалдар келтіріліп, жай бөлшектің жазылу формасы берілген, оқуға үйретіледі. Оқушылар есте сақтау керек: бөлшектің алымы – әйелдік негізгі сан (бір, екі, т.б.), ал бөлгіш – реттік сан (жетінші, жүздік, екі жүз отыз, т.б.).

Мысалға, - бестен бір; - алтыдан екі; - жеті ондық;

сексен үш жүз елу екі. Бөлшек ұғымын бекіту жұмысы барысында оқушыларды «бөлшек» сөзінің шығу төркінімен таныстыру, «алым», «бөлгіш» терминдерін енгізу қажет.

5-сыныпта жай бөлшек, одан кейін ондық бөлшектер туралы түсінік беріледі. Жай бөлшек – жалпы ұғым, ондық бөлшек – нақты. Сондықтан жай бөлшектердің теориялық мәні жоғарырақ, барлық дерлік алгебра жай бөлшектерге құрылған ( ).

Бөлшек сандарды нөмірлеуНатурал және бөлшек сандарды нөмірлеуде кейбір айырмашылықтар бар:

натурал санның бір атауы мен бір белгілеуі болады;

бөлшек санның атаулары мен белгілеулерінің шексіз саны бар.

Мысалы: ;............

Мұның негіздемесі бөлшектің негізгі қасиеті болып табылады, жай бөлшектер ондық бөлшектерден айырмашылығы көп мағыналы оқылады.

Мысалы: бір мың үш жүз елу жеті

Бөлшектердің элементтерін ажыратуға тек екпін мен алым мен бөлгіштің атаулары арасындағы үзіліс ғана мүмкіндік береді.

---

Математиканың қазіргі тұжырымдауындағы «бөлшек» және «бөлшек сан» ұғымдарының арасындағы айырмашылықты берік түсіну міндетті деп санауға тиіс.

Мысалы:

Сұрақтарға жауап бер:

1. 
   осы қатарда неше сан бар? (7)
   
2. 
   осы қатарда неше бүтін сан бар? (2)
   
3. 
   осы қатарда неше бөлшек (бөлшек сандар) бар? (бес)
   
4. 
   Бұл қатарда неше жай бөлшек бар? (3)
   
5. 
   Бұл қатарда неше ондық бар? (2)
   

Жай бөлшек ұғымымен таныстыру

Бөлшек сандарды алудың негізгі көздері 3:

1. 
   бөлшек сандар шамаларды өлшеу нәтижесінде пайда болады;
   
2. 
   объектіні бөліктерге, үлестерге бөлу;
   
3. 
   бөлшек сандар бір санды екінші санға бөлу нәтижесінде пайда болады
   

Жай бөлшектерге амалдар

1. 
   бүтін саннан бөлшекті азайту;
   
2. 
   аралас санның аралас санынан алу, мұнда азайтылғаны азайтылғаннан үлкен;
   
3. 
   барлық әрекеттерге күрделі мысалды қарастыру;
   
4. 
   және т.б......................................
   

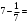
15. Тұрғысынан отбасының ұлы

16. Теңдеулер мен теңдіктерді оқуды меңгерту

Мазмұны

1. 
   Теңдеулер мен теңсіздіктерді шешуге байланысты негізгі үш сала
   
2. 
   Әрбір нақты сыныптағы әртүрлі теңдеулер мен теңсіздіктер сызығын қарастыру
   
3. 
   Теңдеулер мен теңсіздіктерді зерттеудің негізгі кезеңдері
   

1.Теңдеулер мен теңсіздіктерді шешуге байланысты негізгі үш сала. Теңдеулер мен теңсіздіктерге қатысты материал үш негізгі салаға қатысты:

1. 
   теңдеу сөз есептерін шешу құралы ретінде;
   
2. 
   ерекше түрдегі теңдеу, алгебраның зерттеу нысаны қызметін атқаратын формула;
   
3. 
   теңдеу сан жанама түрде анықталатын формула ретінде
   

Теңдеулер сызығы санмен тығыз байланысты, барлық сандық аймақтар кез келген теңдеулерді шешуге байланысты пайда болды. Теңдеулер сызығы да функционалдық сызықпен тығыз байланысты. Жалпы білім беретін мектепте теңдеу бесінші сыныптан бастап оқытыла бастайды және оқушылар есептерді шешудің бірыңғай әдісі – теңдеу әдісін алады.

2. Әр нақты сыныптағы әртүрлі теңдеулер мен теңсіздіктер сызығын қарастыру

---

V сыныпта теңдеудің тек бір бөлігінде белгісіздерді қамтитын теңдеулер шешіледі. Бұл сыныпта теңдеудің анықтамасы берілмейді, мұнда бастауыш сыныптардағы сияқты теңдеулер арифметикалық амалдардың құрамдас бөліктері арасындағы тәуелділіктер негізінде шешіледі, мысалы: 4*(12-х):3+4= 22

6-сыныпта теріс сандарға арифметикалық амалдар оқытылады, бұл сызықтық теңдеулерді мүшелерді бір бөліктен екінші бөлікке көшіру, ұқсас мүшелерді азайту, теңдеудің екі бөлігін де белгісізге коэффициентке бөлу арқылы шешудің жалпы әдісін енгізуге мүмкіндік береді.

Теңдеудің анықтамасы, теңдеудің түбірі туралы түсінік және теңдеуді шешу үшін нені білдіретіні таныстырылады. 6-сыныпта теңдеудің эквиваленттігі туралы түсінік беріліп, мысалдар арқылы түсіндіріліп, сызықтық теңдеу туралы түсінік беріліп, оның түбірлерінің саны туралы мәселе зерттеледі. Теңдеу ұғымына жақын – тұлға ұғымы. 7-сыныпта сәйкестік ұғымы айнымалылардың кез келген мәндеріне сәйкес келетін теңдік арқылы беріледі. 8-сыныпта рационал бөлшектерді қарастыру кезінде сәйкестік ұғымы нақтыланады және келесі анықтама беріледі: сәйкестік дегеніміз оған кіретін барлық рұқсат етілген айнымалылар үшін ақиқат болатын теңдік. 8-сыныпта квадрат теңдеулерді шешу әдістері, толық квадратты ерекшелеу, түбір формуласы, Виет теоремасы, сандық теңсіздіктерді оқу, сызықтық теңсіздіктерді және олардың жүйелерін шешу оқытылады. 9-сыныпта бүтін рационал теңдеу туралы түсінік беріледі, бір белгісізі бар 3, 4 дәрежелі теңдеулерді шешу көбейткіштерге бөлу және көмекші айнымалыны енгізу арқылы зерттеледі. Бір айнымалысы бар бірінші дәрежелі теңсіздіктер интервалдар мен графиктер әдісі негізінде шешіледі, ал 1-ші және 2-ші дәрежелі теңдеулер бар теңдеулер жүйесін шешу алмастыру, қосу және графикалық әдіспен жүзеге асырылады. 10-сыныпта ең қарапайым тригонометриялық теңдеулер қарастырылады: және күрделірек тригонометриялық теңдеулер. Келесі кезекте тригонометриялық теңсіздіктерді шешу жолдарын қарастырамыз.

11-сыныпта көрсеткіштік және логарифмдік теңдеулер оқытылады, иррационал теңдеулер қарастырылады, теңдеулер, теңсіздіктер, жүйелер туралы мағлұматтар жалпыланады, олардың теңдігіне ерекше көңіл бөлінеді.

3. Теңдеулер мен теңсіздіктерді зерттеудің негізгі кезеңдері Теңдеулер мен теңсіздіктер туралы теориялық мәліметтерді беру оқу тақырыптарының мазмұны мен реттілігіне байланысты:

---

Смотрите также файлы

• Сборник тестовых заданий для самостоятельной подготовки слушателей к сертификационному экзамену.doc

• Игра По страницам истории математики.doc

• Работа с циклами.docx

• основы микробиологии, санитарии и гигиены в пищевом производстве.docx

• 11б, 20б Дайте общую характеристику строения атома и укажите основные химические свойства элемента 36 Решение.docx