Файл: Емтихана атысты 1сратар 13. Кпбурыштар. Геометриялы фигураларды аудандары.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 19
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
санау жүйелері;
өрнектердің бірдей түрлендірулері;
функциялары, математикалық талдаудың басы.
Теңдеулер мен теңсіздіктер сызығының мазмұнын кеңейтудің 2 жолы бар:
-
алдымен теңдеулерге, сосын теңсіздіктерге қатысты материал оқытылады. Бірінші жолдың нақты экспозициясы квадрат үшмүшелік теориясына дейін барады. Жоғары сыныптарда логарифмдік, көрсеткіштік және тригонометриялық теңдеулер қарастырылса, теңсіздіктерді зерттеу теңдеумен тығыз байланысты; -
теңсіздіктердің негізгі кластары сәйкес теңдеулерді зерттегеннен кейін бірден зерттеледі. Теңдеулер (теңсіздіктер) теңдеудің сол және оң бөліктерін бейнелейтін функция түріне қарай жіктеледі (теңсіздік). түріндегі теңдеулер (теңсіздіктер). алгебралық деп аталады, егер
алгебралық деп аталады, егер - алгебралық функциялар; функциялардың кем дегенде біреуі болса, трансцендентті
- алгебралық функциялар; функциялардың кем дегенде біреуі болса, трансцендентті - трансценденттік; рационалды, функциялары
- трансценденттік; рационалды, функциялары - рационалды; тұтас ұтымды, егер
- рационалды; тұтас ұтымды, егер - функциялардың ең болмағанда біреуі болса, бүтін рационал, бөлшек рационал
- функциялардың ең болмағанда біреуі болса, бүтін рационал, бөлшек рационал – бөлшек-рационал; иррационал, егер алгебралық функциялардың кем дегенде біреуі болса
– бөлшек-рационал; иррационал, егер алгебралық функциялардың кем дегенде біреуі болса иррационалды болып табылады.
иррационалды болып табылады.
25. Сан ұғымын дамыту
Мазмұны
-
Математика курсында сандарды зерттеудің әртүрлі тәсілдері -
Жаңа нөмірлердің әдістемелік негіздері -
Натурал және бөлшек, оң және теріс сандар
«Сан», «теңдеу», «функция» ұғымдары мектеп математика курсының негізгі ұғымдары болып табылады. Теңдеулер, функциялар сандар жиынында қарастырылатындықтан, сан ұғымы математиканың, алгебраның, алгебраның негізгі математикалық ұғымы және талдаудың бастамасы болып табылады.
Математиканы оқытудың теориясы мен әдістемесінде математиканы оқытатын 1-11-сыныптар аралығындағы сандық жиындарды, олардың қасиеттерін жан-жақты зерттеу жеке мазмұндық-әдістемелік желі – сандарды дамыту желісі түрінде рамкаланады.
Қазіргі математика әртүрлі сипаттағы сандармен айналысады:
N=1; 2; 3; ............ - натурал сандар жиыны
Z – бүтін сандар жиыны
Q=
R=Q
Жетілдірілген математика бойынша:
C=a+bi – күрделі сандар
K - гиперкомплексті сандар
Барлық сандық жиындар қосу қатынасы арқылы байланысқан.
(1) екіншіден (Z) бастап жиын алдыңғы жиынның кеңейтімі болып табылады. Бұл келесі шарттар орындалса, Y X кеңейтімі екенін білдіреді:
-
X жиыны Y жиынының ішкі жиыны; X Сағат
Сағат -
Х жиынының элементтеріне арналған барлық қатынастар мен амалдар У жиынында да анықталған.
Сонымен бірге олардың мағынасы кеңейгенге дейін Х жиынында болған мағынамен сәйкес келеді. Y жиынында операция орындалады, ол Х-та мүмкін емес немесе әрқашан орындала бермейді.
-
Y кеңейтімі бірінші талаптарды қанағаттандыратын барлық мүмкін кеңейтімдердің ең кішісі болып табылады.
Осыған байланысты математиканы оқытудың әртүрлі кезеңдеріндегі сан ұғымы оқушылардың бұрынғы идеяларын бойына сіңіре отырып кеңейіп келеді:
- 5-сыныпта сан әрі натурал сан да, жай бөлшек те, ондық бөлшек те болады;
- 6-сыныпта сан әрі натурал сан да, бүтін сан да, рационал сан да болады;
- 7-сыныпта сан – натурал, бүтін, рационал сан, ол теңдеулерде, теңсіздіктерде, функцияларда шешуші рөл атқарады;
- 8-сыныпта сан әрі рационал, әрі иррационал сандар, ол өзінің геометриялық моделімен нақты сан;
- 9-сыныпта сан – сандар түзуіндегі нақты сан, онда функциялар, теңдеулер, теңсіздіктер оқытылады;
- 10-11 сыныптарда сан – нақты санның, үздіксіздік қасиеті бар, бірақ математикалық талдау элементтері дамыған R жиынының қалыптасқан идеясы.
Студенттердің бейнелеріндегі сан ұғымының кеңеюімен санның қасиеттері мен оларға жасалатын амалдар ауқымы кеңейеді:
- N бойынша «+» және «*» амалдары алгебралық, коммутативтілік, ассоциациялық, үлестірімділік, разрядтық қосу және көбейту жарамды;
- Z бойынша «+», «-», «*» амалдары алгебралық, бүтін сандардың бөлінгіштік теориясы (LCM, GCD, жай, құрама сандар), бүтін сандарды арифметикалық түрлендірулер әзірленуде;
- Q бойынша «+», «-», «*», «:» амалдары алгебралық болып табылады, рационал өрнектерді (жай және ондық бөлшектер) алгебралық түрлендіру теориясы әзірленуде;
- R бойынша «+», «-», «*», «:» амалдары алгебралық, R бойынша+- амалдар – алгебралық, нақты сандарды жуықтау теориясы дамыды, R үздіксіздік қасиеті қалыптасады, үздіксіз элементар функциялар және олардың графиктері зерттеледі;
- С тілінде «+», «-», «*», «:» амалдары алгебралық, күрделі сандардың әртүрлі кескіндері, оларға амалдар зерттеледі, барлық алгебралық теңдеулер шешіледі, түбір алудың көп мағыналылығы пайда болады.
Сандарды енгізу схемасы (А.Н. Колмогоров)Сан ұғымын тізбектей енгізу схемасын қарастырайық
| 1 теріс емес бүтін сандар |


| 5 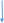 теріс емес рационал сандар теріс емес рационал сандар |
| 3 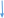 рационал сандар рационал сандар |
| 6 теріс емес нақты сандар |
| 4  алгебралық сандар алгебралық сандар |
| 7  нақты сандар нақты сандар |
| 8 күрделі сандар |
| 2 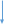  бүтін сан бүтін сан |

I. Алгебра тұрғысынан жалпыламалардың табиғи қатары жолды ұстанады
II. Мектепте жалпылау жолымен жүреді
III.
Сандық сызық мектеп математика курсының ең маңызды бағыттарының бірі ретінде басқа мазмұндық және әдістемелік желілермен тығыз байланыста:
- сандарға амалдар, олардың қасиеттері түрлендіріледі, әріптермен жасалатын амалдарға жалпыланады - алгебралық түрлендірулер, сол арқылы бірдей түрлендірулер сызығы сандар сызығынан ажыратылады;
- әр түрлі сандық жиындардан алынған сандар (N, Z, Q, R), олармен орындалатын амалдар теңдеулерді, теңсіздіктерді құрастыруға, зерттеуге негіз болады, бұл сандар сызығы мен теңдеулер сызығының, теңсіздіктердің, жүйелердің байланысын негіздейді;
- мектептік алгебра курсында және талдаудың басында сандық функциялар оқытылады - R-дан R-ге салыстыру, оларды зерттеу нақты сандарды (максималды, ең төменгі нүктелерді), сандық интервалдарды (период, монотондылық интервалдары) бекітеді, осылайша функциялардың сандық негізі бар, сандық сызық пен функционалдық сызықты қосады.
Мазмұны жағынан да, оқу уақыты жағынан да сан сызығының көлемдік сипаты, оқушылардың математикалық мәдениетін қалыптастырудағы сан ұғымының маңыздылығының жоғары болуы, сандық сызықты оқу мақсаттарының оқу мақсаттарымен салыстырылуын түсіндіреді. жалпы білім беретін мектеп оқушыларына математиканы оқыту.
Нақ сандық қатарда мектеп математика курсының негізгі міндеттері негізінен жүзеге асырылады:
- математикалық білім мен дағды жүйесін меңгеру;
- математиканың идеялары мен әдістері туралы түсініктерін қалыптастыру;
- жеке тұлғаның интеллектуалдық қасиеттерін математика арқылы қалыптастыру және дамыту.
Білім берудің әрбір деңгейінде математиканың жалпы білім беретін курсының бағдарламасында бұл міндеттер дәйекті мақсаттар жүйесі түрінде егжей-тегжейлі берілген:
- 5 - 6 сыныптардың бірінші кезеңінде «математика» мазмұны бойынша сан ұғымын жүйелі түрде дамыту, сандарға ауызша және жазбаша арифметикалық амалдарды орындау дағдыларын дамыту, есептеу дағдыларын дамыту негізгі мақсаттар болып табылады. натурал сандарды, жай және ондық бөлшектерді, оң және теріс сандарды;
- екінші кезеңде 7-9 сыныптарда «Алгебра» курсының мақсаты есептеу және формалды-операциялық алгебралық дағдыларды математика есептерін шешуде сенімді қолдануға мүмкіндік беретін деңгейге дейін дамыту;
Үшінші кезеңде алгебра курсының 10-11 сыныптарында және талдаудың басында R жиыны сандық негіздемесі бар функциялар мен олардың маңызды қасиеттері (монотондылық, периодтылық, үздіксіздік) зерттелетін негізгі жиын болып табылады.

