10. Алгебраические кривые порядка над полем. Кривые второго порядка. Неособые точки кривой и неособые кривые.







11. Эллиптические кривые над полем. Форма Вейерштрасса. Бесконечно удаленная точка. Дискриминант и инвариант эллиптической кривой. Суперсингулярные кривые.













12. Группа точек эллиптической кривой.



13. Эллиптические кривые над конечными полями. Точки конечного порядка. Порядок эллиптической кривой. Неравенство Хассе и его применение.

---

Порядком   точки   на эллиптической кривой называется такое наименьшее натуральное число, что  ; разумеется, такого конечного   может и не существовать, в этом случае мы будем говорить о точке бесконечного порядка. Часто требуется найти точки конечного порядка на эллиптической кривой, в особенности на эллиптических кривых, определенных над полем рациональных чисел  .

Пример 4.4 Найти порядок точки   на  .

Решение. Применяя (4.1), находим, что  ,  . Поэтому   и, следовательно,  . Тем самым порядок   может быть равен 2, 3 или 6. Но  , а если бы   имела порядок 3, то было бы  , что неверно. Итак,   имеет порядок 6.

---

Каждая точка P эллиптической кривой над простым полем Ɛ(Fp ) образует циклическую подгруппу G группы точек эллиптической кривой • Порядок циклической подгруппы группы точек эллиптической кривой (число точек в подгруппе) называется порядком точки эллиптической кривой • Точка P на Ɛ(Fp ) называется точкой порядка q, если: q P=O где q – наименьшее натуральное число, при котором выполняется данное условие







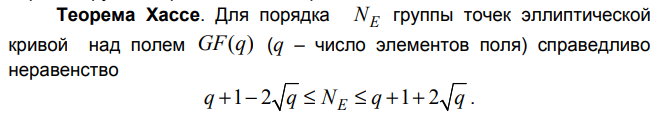
14. Эллиптические кривые над GF(2n ).



Эллиптические кривые в GF(2 в степени n)

Вычисление в группе эллиптической кривой может быть определено в поле GF(2ⁿ). В соответствии с лекциями 5-6, где мы говорили, что элементы множества в этом поле — n -битовые слова, которые можно интерпретировать как полиномы с коэффициентом в GF(2), сложение и умножение этих элементов такое же, как сложение и умножение полиномов. Для того чтобы определить эллиптическую кривую в GF(2ⁿ), необходимо только изменить кубическое уравнение. Общее уравнение

y² + xy = x³ + ax² + b

где  . Обратите внимание, что значение x, y, a и b — полиномы, представляющие n -битовые слова.

Нахождение инверсии

Если P = (x, y), то (–P) = (x, x + y).

Нахождение точек на кривой

Мы можем написать алгоритм для нахождения точек на кривой, используя генераторы для полиномов, которые рассматривали в лекциях 9-10. Но разработку этого алгоритма оставляем как упражнение. Далее следует очень тривиальный пример.

Пример 15.8

Мы выбираем GF (2³) с элементами (0,1, g, g², g³, g ⁴, g⁵, g⁶), использующими неприводимый полином f (x) = x³ + x +1. Этому соответствует полином g³

---

 + g +1 = 0 или g³ = g + 1. Другие степени g могут быть вычислены, как это показано ниже.

0	0	g3 = g + 1	0
1	0	g4 = g2 + g	1
g	0	g5 = g2 + g + 1	1
g2	1	g6 = g2 + 1	1

Используя эллиптическую кривую y² + xy = x³ + g³x² + 1, a = g³ и b = 1, мы можем найти точки на этой кривой, как это показано на рисунке 15.6.




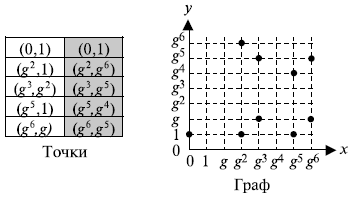
Рис. 15.6. Точки на эллиптической кривой в GF (2 в степени n)

Сложение двух точек

Правила для сложения точек в GF(2ⁿ) немного отличаются от правил GF(p).

1. Если P = (x₁, y₁), Q = (x₂, y₂),  ,  , то R = (x₃, y₃) = P + Q может быть найден как



2.Если Q = P, то R = P + P (или R = 2P ) и может быть найден как



Пример 15.9

Пусть нам надо найти R = P + Q, где P = (0,1) и Q = (g²,1). Мы имеем   и R = (g⁵, g⁴).

Пример 15.10

Пусть нам надо найти R = 2P, где P = (g²,1). Мы имеем   и R = (g⁶, g⁵).

Умножение точек на константу

Для того чтобы умножить точку на константу, точки должны складываться непрерывно согласно правилу R = 2P.

---

15. Алгоритмы сложения и удвоения точек эллиптических кривых.







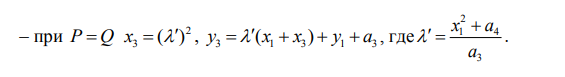
16. Алгоритмы генерации эллиптических кривых и криптографически надежных параметров кривых.



17. Построение псевдослучайных последовательностей на эллиптических кривых.

Введение. Постановка задачи. Псевдослучайные последовательности используются для генерации секретных ключей шифрования, для вычисления цифровой подписи и для работы многих алгоритмов аутентификации. Для построения псевдослучайных последовательностей используются линейные рекуррентные последовательности на эллиптической кривой. Поставим задачу проанализировать существующие генераторы на эллиптической кривой и разработать генератор псевдослучайных последовательностей на эллиптической кривой с использованием квадратичных полей Галуа. Анализ генераторов построенных на точках эллиптической кривой Генератор псевдослучайных последовательностей должен удовлетворять следующим двум требованиям, предложенным в работе: Статистической безопасностью: последовательность, созданная генератором псевдослучайных чисел должна статистически ничем не отличаться от абсолютно случайной последовательности. Криптографической безопасности: возможности зная

---

Смотрите также файлы

• Вариант 1 Задание 2 Прочитайте текст.docx

• Пользуясь приведенными исходными данными, необходимо.docx

• Гайд по подбору витаминов.pdf

• Боевое развертывание сил и средств на пожаре.docx

• Т. Н. Плотникова подпись, дата должность, ученая.docx