-битов последовательности, предсказать следующий или -бит.

Эллиптическая кривая широко используется для построения криптосистем []. Одним из инструментов построения генераторов псевдослучайных последовательностей является эллиптическая кривая над конечным полем.
Следует отметить также статистическую безопасность генератора псевдослучайных чисел, построенного на базе арифметической прогрессии на эллиптической кривой. Она обладает хорошими статистическими свойствами, что показано в работе []: равномерностью распределения элементов арифметической прогрессии для большого , также указан порядок величины отклонения от равномерности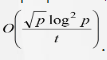

Для случая, при котором известна разность G и старшие биты 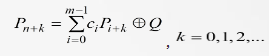в работе Гутиэрехом и Ибиасом предложен эффективный алгоритм нахождения для генераторов, построенных на базе арифметической прогрессий на эллиптической кривой, следовательно, он не обладает криптографической безопасностью. Значит, секретным ключом в генераторе псевдослучайных чисел (1) должны являться . В этом случае не известны эффективные алгоритмы предсказания бит, и генератор (1) является криптографически безопасным. В работе в более общем виде рассмотрены генераторы псевдослучайных последовательностей типа арифметическая прогрессия на эллиптической кривой. Пусть порядок . Последовательность , удовлетворяющих рекуррентному соотношению: , (2),

называют EC-последовательностью порядка

---

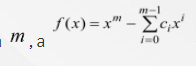– характеристическим многочленом над . Используя обозначения EC-последовательностей, последовательность, заданная формулой (1), называется -последовательностью первого порядка и характеристическим многочленом . О последовательности, заданной формулой (2), известно, что период –последовательности (2) есть делитель периода ее характеристического многочлена . В работе [] показано, что наибольший период имеет примитивный многочлен над полем. Найдем примитивные многочлены второй степени, для чего воспользуемся следующей теоремой.
18. Схема симметричного шифрования на эллиптических кривых.

Зашифрование информации (абонент А защищает сообщение М, предназначенное для абонента В) (рис. 12.1):

А преобразовывает открытый текст М в точки эллиптической кривой;

А выбирает секретный ключ К;

А вычисляет закрытый текст С 

Расшифрование информации (абонент В преобразует закрытый текст С) (рис. 12.2):

В вычисляет обратный ключ (-К).

В восстанавливает открытый текст М 



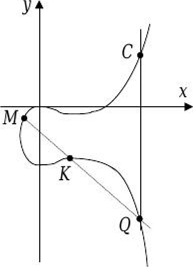
Рис. 12.1.

Прямое преобразование



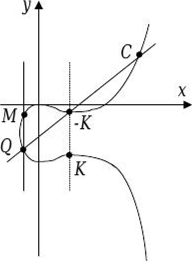
Рис. 12.2.

Обратное преобразование

Пример. Пусть задана кривая Е (СР(23)) вида у2 — X3 + X + 1. Зашифрование информации (абонент А защищает сообщение М, предназначенное для абонента В):

А преобразовывает открытый текст М в точку эллиптической кривой 

---

А выбирает секретный ключ К = (13, 7);

А вычисляет закрытый текст  С

Расшифрование информации (абонент В восстанавливает закрытый текст С, полученный от абонента А):

В вычисляет обратный ключ (-К)



В восстанавливает открытый текст М 

19. Схема асимметричного шифрования на эллиптических кривых.

Реализовать схему асимметричного шифрования на эллиптических кривых.В алгоритмах асимметричного шифрования на эллиптических кривых должны быть определены следующие открытые параметры, общие для всех пользователей:

• 
  конечное поле GF(p);
  
• 
  эллиптическая кривая E(GF(p));
  
• 
  порядок n, который является простым числом;
  
• 
  базовая точка Gпорядка n.
  

1. 
   Процедура генерации ключей осуществляется следующим образом. Каждый пользователь системы генерирует пару ключей следующим образом:
   

• 
  выбирается случайное целое число d, 1 d n1;
  
• 
  вычисляется точка Q dG.
  

Секретным ключом пользователя является число d, открытым ключом – точка

Q.

2. 
   Действия отправителя сообщения (абонент Aшифрует сообщение М,
   

предназначенное для абонента B):

• 
  Авыбирает случайное целое число k, 1 k n1;
  
• 
  Авычисляет точку (x₁, y₁)  kG;
  

---

• 
  Ввосстанавливает исходное сообщение M c₁  x₂ .
  

20. Схема цифровой подписи на эллиптических кривых.





21. Схема распределения ключей на эллиптических кривых.





22. Схема гибридного шифрования на эллиптических кривых.







23. Стандарт ЭЦП ГОСТ Р 34.10-2012

https://protect.gost.ru/v.aspx?control=8&baseC=-1&page=0&month=-1&year=-1&search=&RegNum=1&DocOnPageCount=15&id=172255&pageK=8074B207-9954-40FD-912E-20E8D0BFAA2E

http://elib.osu.ru/bitstream/123456789/11745/1/92829_20190327.pdf

---

Смотрите также файлы

• Вариант 1 Задание 2 Прочитайте текст.docx

• Пользуясь приведенными исходными данными, необходимо.docx

• Гайд по подбору витаминов.pdf

• Боевое развертывание сил и средств на пожаре.docx

• Т. Н. Плотникова подпись, дата должность, ученая.docx