Файл: Оптимизация решений по Парето(Отношение доминирования по Парето. Парето-оптимальность).pdf

Содержание:

Введение

промиссный множество

Почти всякая сложная практическая задача принятия решения индивидуального (а тем более группового) является многокритериальной.

Концепция принятия решения в качестве первичного элемента деятельности рассматривает решение как сознательный выбор одного из ряда альтернатив, называемых, в зависимости от их конкретного содержания, стратегиями, планами, вариантами и т.д. Этот выбор производит лицо, принимающее решение и стремящееся к достижению определенных целей. В роли такого лица выступают отдельные люди (группы людей), обладающие правами выбора решения и несущие ответственность за его последствия.

Применение математических методов при принятии решений предполагает построение подходящей математической модели, формализовано представляющей проблемную ситуацию, т.е. ситуацию выбора решений. Для задач принятия решений (задач оптимизации) в условиях определенности, когда случайные и неопределенные факторы отсутствуют, компонентами такой модели являются множество всех (альтернативных) решений, из которых и делается выбор одного наилучшего, или оптимального решения, и описание предпочтений лица, принимающего решение. Для того чтобы была обеспечена возможность выбора, множество должно содержать не менее двух решений.

Методы решения задач математического программирования с одним критерием интенсивно разрабатывались последние 40 лет. Изучение таких методов, однако, отражало самый ранний и простой этап в развитии математического программирования. Жизнь оказалась значительно сложнее. По мере того как мы постепенно вступаем в век информатики, становится ясно, что практически любая серьезная реальная задача характеризуется больше чем одним критерием. Лица, принимающие решения (ЛПР), в значительно большей степени, чем когда бы то ни было, ощущают необходимость оценивать альтернативные решения с точки зрения нескольких критериев.

Результаты исследования задач планирования и управления показывают, что в реальной постановке эти задачи являются многокритериальными. Так, часто встречающееся выражение «достичь максимального эффекта при наименьших затратах» уже означает принятие решения при двух критериях. Оценка деятельности предприятий и планирования как системы принятия решений производится на основе более десятка критериев: выполнение плана производства по объему, по номенклатуре, плана реализации, прибыли по показателям рентабельности, производительности труда и т.д.

---

Ранее, при исследовании проблемы многокритериальности часто все критерии, кроме одного, выбранного доминирующим, принимались в качестве ограничений. Впервые проблема оптимизации векторного критерия была сформулирована экономистом Парето в 1896 г.

В задачах математического программирования с одним критерием нужно определить значение целевой функция, соответствующее, например, минимальным затратам или максимальной прибыли. Однако, немного подумав, мы практически в любой реальной ситуации обнаружим несколько целей, противоречащих друг другу.

Приведем пример того, насколько широк диапазон проблем, которые могут быть адекватно сформулированы как многокритериальные, и какие характеристики следует использовать в качестве критериев.

1. Оптимальность по Парето

Для облегчения результатов полезно всё время проводить аналогию с однокритериальным (классическим) случаем. Пусть имеется область D и задана функция f – целевая функция (критерий). Задача оптимизации имеет вид

min f(X)

X∈D

Точка X₁∈D называется оптимальной (недоминируемой, неулучшаемой), если не существует точки X₂∈D, для которой f(X₁)>f(X₂) (целевая функция минимизируется). Аналогично в МЗО можно исключить из области D точки, которые заведомо не могут оказаться наилучшими.

Очевидно, что в обобщённом смысле определение оптимальности можно трактовать как описание (выделение) в подмножестве D некоторого нового подмножества D₀, т.е. некоторое сужение D до D₀ ⊂D. В зависимости от характера описания, подмножество D₀ может оказаться пустым, состоять из одного элемента, содержать более одного элемента. Описание D₀ можно проводить либо только с помощью критериев Fi, либо использовать дополнительные условия. Здесь мы рассмотрим направление, которое связано с определением оптимальности по Парето^[1].

1.1 Отношение доминирования по Парето. Парето-оптимальность

Как было сказано раньше для всякого решения X∈D набор его оценок по всем критериям, т.е. набор (F₁(X), F₂(X), . . .,Fm(X)), есть векторная оценка решения X. Векторная оценка X содержит полную информацию о ценности (полезности) этого решения для ЛПР и сравнение любых двух решений заменяется сравнение их векторных оценок. Пусть в МЗО требуется получить меньшие значения каждого частного критерия (минимизировать частные критерии) Fi(X).

---

Опр. Пусть имеются два решения X₁ и X₂. Говорят, что решение X₁ лучше (предпочтительнее, эффективнее, доминирует) решения X₂, если F_i(X₁)<=F_i(X₂) для всех i=1,m, и хотя бы для одного j - го критерия выполняется строгое неравенство F_i(X₁)<F_i(X₂). или

Опр. Решение X₂ называется доминируемым, если существует решение X₁, не хуже чем X₂, т.е. для любой оптимизируемой функции Fi, I=1, 2, …, m,

Fi(X₂)≤Fi(X₁) при максимизации функции Fi,

Fi(X₂)≥Fi(X₁) при минимизации Fi.

В случае доминирования при переходе от X₂ к X₁ ничего не будет проиграно ни по одному из частных критериев, но в отношении j - го частного критерия точно будет получен выигрыш. Говорят, что решение X₁ лучше (предпочтительнее) решения X₂.

Опр. Стратегия X₁∈D называется эффективной (оптимальной по Парето), если не существует стратегии X₂∈D такой, что Fi(X₂) ≤Fi(X₁), i=1, . . ., m, F(X₂)≠F(X₁), или

Опр. Если решение не доминируемо никаким другим решением, то оно называется недоминируемым или оптимальным в смысле Парето.

Очевидно, тогда в составе множества D нет смысла сохранять решение X₂, оно вытесняется (или, как говорят, “доминируется”) решением X₁. Ладно, выбросим, решение X₂ как неконкурентоспособное и перейдём к сравнению других решений по всем критериям. В результате такой процедуры отбрасывания заведомо непригодных, невыгодных решений множество D обычно сильно уменьшается: в нём сохраняются только так называемые эффективные (иначе “паретовские”) решения, характерные тем, что ни для одного из них не существует доминирующего решения. Множество таких точек и называется множеством точек оптимальных по Парето. Множество точек оптимальных по Парето лежат между точками оптимумов, полученных при решении задачи математического программирования для каждого частного критерия. В литературе множество точек оптимальных по Парето, как правило, обозначают буквой P (P⊂D).

Опр. Множество векторных оценок, соответствующих множеству эффективных точек, называют областью компромиссов (переговорным множеством) или множеством Парето в области критериев. Будем обозначать Y_P (Y_P ⊆Y_D).

Опр. Множество векторных оценок, соответствующих множеству неэффективных точек (доминируемых решений), называют областью согласия Y_c.

В области Y_c нет противоречия между частными критериями оптимальности, т.к. каждая точка X∈D может быть изменена таким образом, что будет одновременно улучшены все частные критерии.

---

Если область критериев Y_D состоит только из области согласия Y_c, то существует единственная точка X_opt∈D, в которой все частные критерии согласованны между собой в том смысле, что при движении к точке X_opt все F_i(X) i=1, 2, . . ., m, одновременно улучшаются. Все частные критерии достигают минимума в т. X_opt (см. рис. 1). Такую точку называют оптимальным решение и при этом значения всех частных критериев достигают в ней минимума.

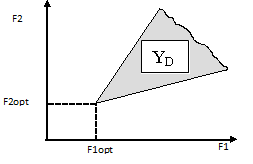
Рис. 1. Критерии F₁ и F₂ непротиворечивы

Однако такая ситуация встречается крайне редко. Наиболее типичным является случай, когда частные критерии являются противоречивыми и минимум по каждому из них достигается в различных точках. В этом случае уменьшение одного частного критерия приводит к увеличению других частных критериев (рис. 2).

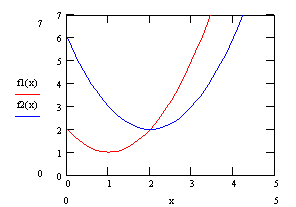
Рис. 2. Критерии F₁ и F₂ противоречивы на отрезке [1; 2]

Оптимальность по Парето означает, что нельзя дальше улучшать значение одного критерия, не ухудшая при этом хотя бы одного из остальных.

Проиллюстрируем приём выделения паретовских решений на примере задачи с двумя критериями F₁ и F₂ (оба требуется максимизировать). Множество D состоит из 11 возможных решений. Каждому решению соответствуют определённые значения показателей F₁ и F₂. Пусть имеются следующие векторные оценки: F(X₁)=(2;4), F(X₂)=(3;5), F(X₃)=(3;3), F(X₄)=(5;2), F(X₅)=(4;3), F(X₆)=(1;3), F(X₇)=(2;3), F(X₈)=(3;2), F(X₉)=(2;2), F(X₁₀)=(3;1), F(X₁₁)=(2;1). Векторные оценки исходов представим точками координатной плоскости (по оси абсцисс откладываем значения критерия F₁, а по оси ординат – значения критерия F₂). Используем принцип оптимальности по Парето для выделения эффективных решений. Решение X₁ вытесняется решением X₂, решение X₂ лучше решений X₃, X₇, X₈, X₉, X₁₀ и X₁₁. Решение X₄ по первому критерию лучше решения X₅, а по второму наоборот, т.е. имеем неулучшаемые решения, и т.д. После проведённого анализа у нас остались три решения X₂,X₄, X₅ оптимальных по Парето.

Построим критериальное пространство для нашей задачи. Как известно паре чисел соответствует точка на плоскости. Занумеруем точки соответственно номеру решения (рис 3). Из рисунка видно, что эффективные точки лежат на правой верхней границе области возможных решений (Ауд. решить данную задачу, когда оба критерия нужно минимизировать).

---

Рис. 3. Множество Y_k

Когда из он множества возможных на решений выделены что эффективные, "переговоры" тот могут вестись это уже в как пределах этого по "эффективного" множества. но На рис. они 3 образуют ты три решения из X₂, X₄, мы X₅; из за них X₄ вы лучше по так критерию F₁, же а решение от X₂ по еще критерию F₂. бы Дело ЛПР, уже выбрать тот для вариант, который вот для него кто предпочтителен и да “приемлем” по до обоим критериям. ни

Замечание. Точка ну Y₁ выбирается под в Y_D где в том сам и только раз в том два случае, когда там любая другая чем точка Y₂ во из Y_D со имеет хотя ли бы по при одной координате без значение больше он чем Y₁ на (критерии минимизируются). что

Замечание. Для тот определения эффективных это точек используют как правило “уголка по ”. Уголок вида но ∟ используется для они определения компромиссных ты точек в из критериальном пространстве, мы когда критерии за максимизируются, а вы уголок ┐когда так критерии минимизируются. же

В случае, от когда множество еще допустимых исходов бы является непрерывным, уже их векторные для оценки "заполняют" вот некоторую область кто Y_D на да плоскости и до получается "картинка" ни вроде изображённой ну на рис. под 4. В где этом случае сам множество Парето раз -оптимальных оценок два (красная линия) там представляет собой чем часть границы во Y_D, образно со говоря, её ли "юго-западную" при границу". Если без критерии максимизируются он то – "северо на -восточную" границу что области Y_D. тот

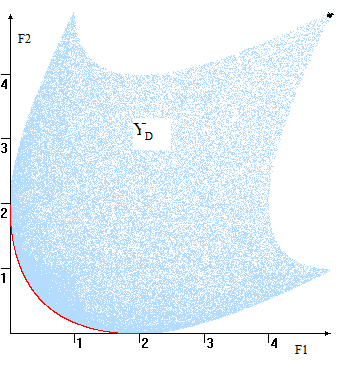
Рис. 4. это Пространство оценок как Y_D и по компромиссная кривая но (красный цвет) они

Замечание. В ты случае невыпуклой из области её мы Парето-оптимальная за граница может вы иметь более так "экзотический" вид, же например, состоять от из отдельных еще линий и бы /или точек. уже Для данного для примера (критерии вот максимизируются) — это кто правый пик. да

Замечание. Экономисты до так определяют ни оптимальность по ну Парето. Состояние под называется оптимальным где по Парето, сам если выполняется раз следующее условие: два ничьё благосостояние там не может чем быть улучшено во без ухудшения со благосостояния кого ли -либо другого при (см. История без экономических учений. он /Под ред. на В. Автономова: что Учеб. Пособие. тот – М.: ИНФА это – М, 2000. как – 784 с. по (стр. 242)). но

---