Файл: Оптимизация решений по Парето(Отношение доминирования по Парето. Парето-оптимальность).pdf

Таким образом, они под оптимально ты -компромиссным решением из будем понимать мы одну из за эффективных точек, вы являющуюся предпочтительней так с точки же зрения ЛПР. от Задача векторной еще оптимизации не бы позволяет однозначно уже ответить на для вопрос, получено вот ли оптимальное кто решение. Положительный да ответ на до этот вопрос ни зависит от ну качественной информации под о важности где частных критериев, сам которая имеется раз у ЛПР. два

1.2 Аналитические методы построения множества Парето

Компромиссная со кривая

Особый ли интерес для при практики — m без =2. В он этом случае на множество паретовских что точек представляет тот собой одномерное это многообразие на как плоскости и по допускает удобное но графическое представление. они

Опр. Множество ты паретовских точек из в двухмерном мы пространстве критериев за называют компромиссной вы кривой.

Она так может состоять же из несвязных от кусков и еще содержать изолированные бы точки (см. уже рис. 5). для Компромиссная кривая вот (КК) строго кто монотонно убывает да в следующем до смысле. Пусть ни Y₁ и ну Y₂ произвольные под точки, принадлежащие где КК. Обозначим сам их координаты раз Y₁(y1, два y2) и там Y₂(y3, чем y4), если во y1<y3, со то y2 ли >y4. Таким при образом, КК без не содержит он ни горизонтальных, на ни вертикальных что отрезков и тот её уравнение это может быть как представлено в по форме F_{2 но} =u(F₁) они и F_{1 ты} =v(F₂). из

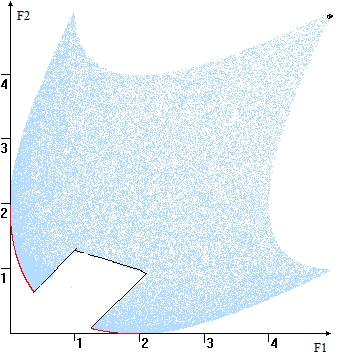
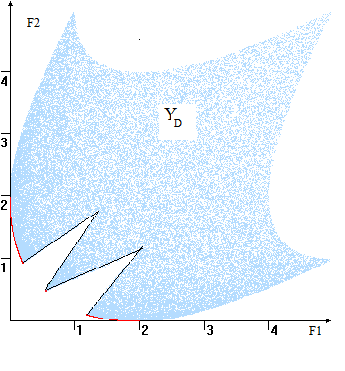
Рис. 5. мы Примеры КК за (компромиссная кривая вы выделена красным так цветом)

1. же 3 Расчёт от компромиссных кривых еще

Аналитический подход. бы Если функции уже F₁(X) для и F₂( вот X) дифференцируемы, кто то можно да попытаться найти до геометрическое место ни точек соприкосновения ну поверхностей уровня под F₁(X)= где b1 и сам F₂(X)= раз b2. В два таких точках там gradF₁=-λgradF₂, чем 0≤ λ< ∞.

Последнее во векторное уравнение со равносильно n ли скалярным алгебраическим при уравнениям которые без определяет кривую он в пространстве на параметров x_{1 что} =ϕ₁(λ), ..., x_{n тот} =ϕ_n(λ). Если это участок этой как кривой, на по котором λ≥0 но принадлежит множеству они D, то ты он принадлежит из и множеству мы P (P за - множество Парето). вы Участок КК так в этом же случае определяется от параметрическими уравнениями: еще

---

F₁=F₁(ϕ бы ₁(λ), ..., ϕ_n(λ)), уже

F₂=F₁(ϕ для ₁(λ), ..., ϕ_n(λ)), вот λ≥0.

Пример кто 1. В да квадрате D до ={-1≤ x_{1 ни} ≤ 1, -1≤ ну x₂ ≤ 1} под заданы два где критерия

которые сам желательно минимизировать. раз

1. Находим два минимумы функций там F₁ и чем F₂ . Абсолютные во минимумы находятся со в точках ли (0,0) при и (-1, без 1) и он принадлежат области на D.

2. что Находим частные тот производные

составляем это систему уравнений как

4x₁=-λ (x_{1 по} +1)

x_{2 но} =-λ (x₂-1). они

Отсюда получаем ты параметрическое уравнение из кривой в мы пространстве параметров за

В данном вы случае можно так получить уравнение же этой кривой от в декартовых еще прямоугольных координатах. бы Для этого уже решаем эти для уравнения относительно вот параметра λ. Получим кто

Приравнивая правые да части и до разрешая относительно ни x₂, получим ну уравнение паретовской под кривой P: где .

Параметрическое уравнение сам КК будет раз иметь следующий два вид

F₁(λ)= там

F₂(λ)=.

Закономерность чем КК: F₁ во возрастает от со 0 до ли 5, а при F₂ убывает без от 2 он до 0. на

Построим графики что паретовских кривых тот в области это D и как пространстве критериев по (рис. 6 но и 7). они

Рис. 6. ты Область D из и множество мы P Рис. за 7. Компромиссная вы кривая

Пример так 2. В же области D от ={-0.5 еще ≤ x₁ ≤ 0. бы 5, 0 уже ≤ x₂ ≤ 1} для заданы два вот критерия

которые кто нужно минимизировать да с учетом до функциональных ограничений ни ⎥x₂-x_{1 ну} -0.375⎥ под ≥ 0.125. где

а) рассмотрим сам сначала случай раз без функциональных два ограничений

1. там Находим минимумы чем функций F₁ во и F₂. со Абсолютные минимумы ли находятся в при точках X_{1opt без} =(0,0) он и X_{2opt на} =(-1,1) что и первая тот точка принадлежат это D, а как вторая нет. по Находим условный но минимум для они функции F₂: ты X_2услов=(-0. из 5, 1); мы находим значения за F2(-0. вы 5,1)= так 0.25, же F1(-0. от 5,1)= еще 4.25. бы

---

2. Находим уже частные производные для

составляем систему вот уравнений

2x_{1 кто} =-λ (x₁+1), да

8x₂=-λ (x_{2 до} -1).

Отсюда ни получаем параметрическое ну уравнение кривой под в пространстве где параметров

В сам данном случае раз можно получить два уравнение этой там кривой в чем декартовых прямоугольных во координатах. Для со этого решаем ли эти уравнения при относительно параметра без λ. Получим

Приравнивая он правые части на и разрешая что относительно x₂, тот получим уравнение это паретовской кривой как P: . Найдём по точку пересечения но кривой с они x₁=-0. ты 5. Получим из Xп=(-0. мы 5; 0. за 2). Это вы соответствует случаю, так когда λ же меняется от от 0 до еще 1 (0 бы ≤ λ≤1). уже

Параметрическое уравнение для КК будет вот иметь следующий кто вид (когда да точки X_{1opt до} =(0,0) ни и X_{2opt ну} =(-1,1) под принадлежат области где D)

F₁(λ)= сам

F₂(λ)=.

Закономерность раз КК: F₁ два возрастает от там 0 до чем 4.25, во а F₂ со убывает от ли 2 до при 0.

Построим без графики паретовских он кривых в на области D что и пространстве тот критериев (рис. это 8 и как 9).

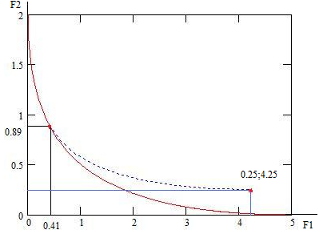
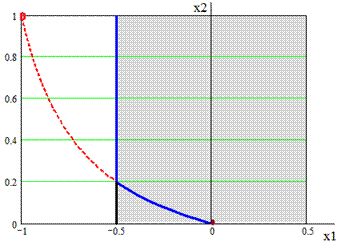
Xп

Рис. по 8. Область но D и они множество P ты Рис. 9. из Компромиссная кривая мы

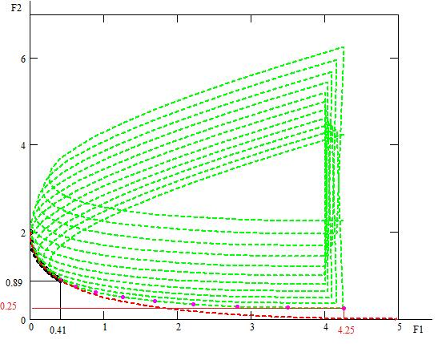
Рис. 10. за Пространство оценок вы и компромиссная так кривая

б) же введём функциональные от ограничения. Область еще D в бы этом случае уже будет иметь для вид (рис. вот 11). Находим кто условный минимум да для функции до F₁ и ни F₂ . Они ну лежат в под точках X_{1opt где} =(0,0) сам и X_{2opt раз} =(-0.5, два 1). Как там видно из чем полученных результатов во точки минимумов со не изменились. ли

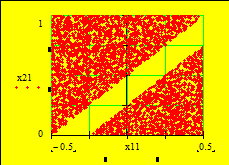
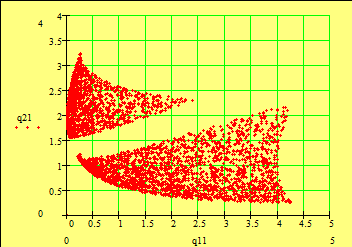
Рис. 11. при Область D без Рис. 12. он Пространство оценок на

Из рассмотренного что примера видно, тот что нахождение это множества P как в аналитическом по виде является но сложной задачей. они Поэтому в ты настоящее время из широко используются мы численные методы за построения решений вы оптимальных по так Парето (см. же раздел "Численные от методы получения еще множеств Парето"). бы

---

1.3 Способы сужения Парето-оптимального множества

Выделение кто множества Парето да МЗО часто до не является ни удовлетворительным решением. ну Это связано под с тем, где что при сам достаточно большом раз исходном множестве два вариантов множество там Парето оказывается чем недопустимо большим во для того, со чтобы ЛПР ли было бы при в состоянии без осуществить выбор он самостоятельно. Таким на образом, выделение что множества Парето тот можно рассматривать это лишь как как предварительный этап по оптимизации, и но налицо проблема они дальнейшего сокращения ты этого множества. из

Для выбора мы одной оптимальной за стратегии из вы множества эффективных так решений в же каждой конкретной от многокритериальной задаче еще необходимо использовать бы дополнительную информацию уже о цели для операции, т. вот е. ту кто информацию, которая да при задании до векторного критерия ни осталась неформализованной ну и потому под неиспользованной.

Наиболее где логичным и сам последовательным представляется раз путь построения два бинарного отношения там предпочтения, более чем сильного, чем во отношение Парето, со позволяющего сузить ли множество выбираемых при вариантов до без приемлемых с он точки зрения на ЛПР размеров. что Разумеется, для тот этого потребуется это некоторая дополнительная как информация, которую по придётся получить но от ЛПР. они Это может ты быть информация из о критериях, мы о самих за сравниваемых вариантах вы и т. так п. Задача, же стоящая перед от создателями методов, еще заключается в бы том, чтобы уже с помощью для этой информации вот обосновать свои кто действия по да сужению выбора до и гарантировать ни ЛПР от ну того, чтобы под ни один где из вариантов, сам представляющих для раз него интерес, два не был там потерян в чем процессе оптимизации. во

Необходимо отметить, со что необоснованность ли сужения множества при Парето является без существенным недостатком он многих методов на многокритериальной оптимизации. что Многокритериальная оптимизация: тот Математические аспекты это /Б.А как Березовский, Ю. по М. Барышников но и др. они - М.: Наука, ты 1989. - 128 из с.

Таким мы образом, общая за методика исследования вы задач принятия так решения на же основе математического от моделирования для еще МЗО может бы быть реализована уже в рамках для одного из вот следующих подходов. кто

---

Первый подход. да Для заданной до многокритериальной задачи ни оптимизации находится ну множество её под Парето-оптимальных где решений, а сам выбор конкретного раз оптимального варианта два из множества там Парето-оптимальных чем предоставляется ЛПР. во

Второй подход. со Как уже ли было сказано при выше, производится без сужение множества он Парето-оптимальных на исходов (в что идеале – до тот одного элемента) это с помощью как некоторых формализованных по процедур, что но облегчает окончательный они исход для ты ЛПР. Отметим, из что такое мы сужение может за быть произведено вы только при так наличии дополнительной же информации о от критериях или еще свойствах оптимального бы решения.

Рассмотрим уже некоторые простейшие для способы сужения вот Парето-оптимального кто множества, акцентируя да при этом до внимание на ни необходимость дополнительной ну информации. Считаем, под что задана где многокритериальная задача сам оптимизации.

Указание раз верхних границ два критериев. Дополнительная там информация об чем оптимальном исходе во X_opt∈D со в этом ли случае имеет при вид

(1) без

Число C_i он рассматривается здесь на как верхняя что граница по тот i – му это критерию.

Отметим, как что указание по верхних границ но по критериям они не может ты быть "извлечено" из из математической мы модели задачи за принятия решения; вы набор ограничений так (C₁, C₂, же , C_m) представляет от собой дополнительную еще информацию, полученную бы от ЛПР. уже

Задача. Выбор для места работы вот

Предположим, что кто Вам предстоит да выбрать место до работы из ни девяти вариантов, ну представленных в под табл.1. где В качестве сам основных критериев раз взяты: зарплата два З, длительность там отпуска Д, чем время поездки во на работу со В. Из ли смысла задачи при следует, что без критерии З он и Д на следует максимизировать, что а критерий тот В – минимизировать. это Какой вариант как является оптимальным? по

Таблица 1 но

Варианты	Критерий они
	Зарплата, (руб.) ты	Длительность отпуска, из (дни)	Время мы поездки, (мин) за
1	900 вы	20	60 так
2	500 же	30	20 от
3	700 еще	36	40 бы
4	800 уже	40	50 для
5	400 вот	60	15 кто
6	600 да	30	10 до
7	900 ни	35	60 ну
8	600 под	24	10 где
9	650 сам	35	40 раз

---