Файл: Выполнение практических заданий по дисциплине математика Группа Студент В.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.03.2024
Просмотров: 21
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. Выполнить деление комплексных чисел
2. Вычислить пределы последовательностей
3. Используя признаки Даламбера и Коши исследовать сходимость рядов
5. Вычислить неопределенный интеграл
6. Найти частные производные первого и второго порядка
11. Для заданных векторов найти смешанное произведение [ ⃗????⃗ × ????⃗ ] ∙ ⃗????
Автономная некоммерческая организация высшего образования
«МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»
Кафедра Государственного и муниципального управления
Форма обучения: Дистанционная
ВЫПОЛНЕНИЕ
ПРАКТИЧЕСКИХ ЗАДАНИЙ
ПО ДИСЦИПЛИНЕ
Математика
Группа
Студент В.В.Грачев
МОСКВА 2022
Практические задания Задачи:
1. Выполнить деление комплексных чисел
1.1
1.2
2. Вычислить пределы последовательностей
2
???? ????
2.2.
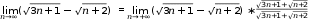 =
= =
????
????
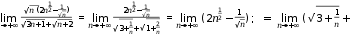
3. Используя признаки Даламбера и Коши исследовать сходимость рядов
3.1.

Применим сравнительный признак: α=-3.
Поскольку α меньше 1, то ряд расходится.
????
3.2.
2????+1

П
Поскольку полученное значение равно 1, то получаем неопределенность.
Признак Даламбера.
????+1

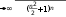
????lim = ????lim→∞
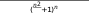 = ????lim→∞ 2∗(????2+2)???? =
= ????lim→∞ 2∗(????2+2)???? = 2
Поскольку q = 1, то получаем неопределенность.
???? ????
Рассмотрим предел исходного ряда. lim (
 ∗ ???? + 1) ≠ 0
∗ ???? + 1) ≠ 0 ????→∞ 2
Данный предел не равен 0. Необходимое условие сходимости не выполняется, следовательно, ряд расходится.
-
Найти производные сложных функций 4.1. y = sin (ln x) = (ln(sinx)) = 1 *sin x = ( 1 )*cos x = ctgх.
1 *sin x = ( 1 )*cos x = ctgх.
sin x sin x

 4.2.
4.2.  ???? ???????? ????16 = ???? ???????? ???? ∗
???? ???????? ????16 = ???? ???????? ???? ∗  ???? ????6
???? ????6???????? ???????? ???????? ???? 6 ????
6????
5. Вычислить неопределенный интеграл
5.1. ∫ ????3 sin 2???? ???? ????
C -
5.2. ∫ ????2 2???? ???? ????
6. Найти частные производные первого и второго порядка
6.1. z = ????3????41cos???? = sec????3????(????4) ???? sec????????(????) (3????−3) ???? ∗????????(????????34)∗ sec (????) = ???????? (????) ∗sec(????(????)∗????23−34????3−1∗sec (????) =
 ∗????
∗????= 2 3) ∗????
(????4)
???????? (????) ∗sec(????)∗????3−3????2∗sec (????)
 2∗3∗????4 (????4)2∗????6 =
2∗3∗????4 (????4)2∗????6 = ????
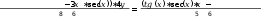
(???????? (????) ∗sec(????)∗????3 2 3 3 3????2∗sec(????))∗4
???? ∗???? ???? ∗????
???????? sin (????) 3
 = 3????4cos ????2 − ????4????4cos ????
= 3????4cos ????2 − ????4????4cos ???? ???????? ????
???????? 4
 = −
= −  3????5cos ????
3????5cos ???? ???????? ????
′
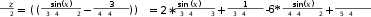
????2 2 12
???????? ???? ???? cos ???? ???? ???? cos???? ???? ???? cos???? ???? ???? cos ???? ???? ???? cos???? ???? ???? cos ????
????
????2???? 4 ′ 20

???????? ???? ∗???? ∗cos(????)
6.2.
z
???????? ???????? ????????
Производная от у по у равна 1: ????????
????????
Производная постоянной равна нулю: ????????−1 + ????????−1 ∗ ????????(????) ∗ ????

 ???????? ???? ∗ ????
???????? ???? ∗ ???? = ????
???????? ????
 ???????? ???? ∗ ????????(????) = ????
???????? ???? ∗ ????????(????) = ????????????

????2???? ???? ′
????????2 ???? ????
????2????

????
????????2 ???? ∗ ????????2
= (???????? ∗ ????????(????))′
 ????????2 ???? = ???????? ∗ ????????(????)2
????????2 ???? = ???????? ∗ ????????(????)2 | 7.1. A + B = (1 3 | + (−1 ) 1 | = (1 + (−1) ) 3 + 1 | + 2 = (0 ) + 4 4 | 4 ) 8 |
7.2. A + B = (−8 −3) + (−1 −1) = (−9 −4)
−2 −6 −1 −1 −3 −7
8. Найти произведение матриц
8.1. A * B = ( 0 1) * (2 5) = ( 0 1 )
−2 3 0 1 −4 −7
8.2. A * B = (6 2) * (0 −6) = (10 −22)
3 8 5 7 40 38
9. Найти определители матриц
9.1. A = (3 1) = 3*3 – 2*1 = 9–2 = 7
2 3
9.2. A = (3 6) = 3*7 – 5*6 = 21–30 = –9
5 7
10. Решить систему уравнений
7???? + 2???? = 15 7???? + 2???? = 15 7???? + 2???? = 15 7???? + 2???? = 15

10.1. { { {

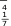 7
7{
???? = −
 ???? = − ???? = −
???? = − ???? = − 9???? = 11???? + 5 9???? − 11???? = 5 −
 ???? = −1
???? = −110.2. { { {
6???? = 12???? − 8 − (12????) + 6???? = −8 − (12????) + 6???? = −8
????
−
 = −1 13???? = 2 ???? =
= −1 13???? = 2 ???? ={
− (6????) + 3???? = −4 − (6????) + 3???? = −4 − (6????) + 3???? = −4
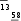
???? =???? =
{ {
−
11. Для заданных векторов найти смешанное произведение [ ⃗????⃗ × ????⃗ ] ∙ ⃗????
11.1. ???? = (1; -2; 1) ????⃗ = (2; 1; -2) ???? = (1; 1; 1)
1·1·1 + (-2)·(-2)·1 + 1·2·1 - 1·1·1 - (-2)·2·1 - 1·(-2)·1 = 1 + 4 + 2 - 1 + 4 + 2 = 12
11.2. ???? = (1; 1; 2) ????⃗ = (1; -1; 3) ???? = (-2; -2; 2)
1·(-1)·2 + 1·3·(-2) + 2·1·(-2) - 2·(-1)·(-2) - 1·1·2 - 1·3·(-2) = -2 - 6 - 4 - 4 - 2 + 6 = -12
