Файл: 1 мод ответы мво.doc

Характеристики алгоритма JPEG: Коэффициенты компрессии: 2-200 (Задается пользователем).

Класс изображений: Полноцветные 24 битные изображения или изображения в градациях серого без резких переходов цветов (фотографии).

Симметричность: 1

Характерные особенности: В некоторых случаях, алгоритм создает “ореол” вокруг резких горизонтальных и вертикальных границ в изображении (эффект Гиббса). Кроме того, при высокой степени сжатия изображение распадается на блоки 8х8 пикселов.

CCIT- алгоритм сжатия изображения

Алгоритм Хаффмана с фиксированной таблицей CCITTGroup 3

Близкая модификация алгоритма используется при сжатии черно-белых изображений (один бит на пиксел). Полное название данного алгоритма CCITT Group 3. Это означает, что данный алгоритм был предложен третьей группой по стандартизации Международного Консультационного Комитета по Телеграфии и Телефонии (Consultative Committee International Telegraph and Telephone). Последовательности подряд идущих черных и белых точек в нем заменяются числом, равным их количеству. А этот ряд, уже в свою очередь, сжимается по Хаффману с фиксированной таблицей.

Определение: Набор идущих подряд точек изображения одного цвета называется серией.Длина этого набора точек называется длиной серии.

В таблице, приведенной ниже, заданы два вида кодов:

• Коды завершения серий — заданы с 0 до 63 с шагом 1.

• Составные (дополнительные) коды — заданы с 64 до 2560 с шагом 64.

Каждая строка изображения сжимается независимо. Мы считаем, что в нашем изображении существенно преобладает белый цвет, и все строки изображения начинаются с белой точки. Если строка начинается с черной точки, то мы считаем, что строка начинается белой серией с длиной 0. Например, последовательность длин серий 0, 3, 556, 10, ... означает, что в этой строке изображения идут сначала 3 черных точки, затем 556 белых, затем 10 черных и т.д.

На практике в тех случаях, когда в изображении преобладает черный цвет, мы инвертируем изображение перед компрессией и записываем информацию об этом в заголовок файла.

Алгоритм компрессии выглядит так:

for(по всем строкам изображения) {      Преобразуем строку в набор длин серий;      for(по всем сериям) {          if(серия белая) {              L= длина серии;              while(L > 2623) { // 2623=2560+63                  L=L-2560;                  ЗаписатьБелыйКодДля(2560);              }              if(L > 63) {                  L2=МаксимальныйСостКодМеньшеL(L);                  L=L-L2;                  ЗаписатьБелыйКодДля(L2);              }              ЗаписатьБелыйКодДля(L);              //Это всегда код завершения          }          else {              [Код аналогичный белой серии,              с той разницей, что записываются              черные коды]          }      }      // Окончание строки изображения  }

---

Поскольку черные и белые серии чередуются, то реально код для белой и код для черной серии будут работать попеременно.

В терминах регулярных выражений мы получим для каждой строки нашего изображения (достаточно длинной, начинающейся с белой точки) выходной битовый поток вида:

((<Б-2560>)*[<Б-сст.>]<Б-зв.>(<Ч-2560>)*[<Ч-сст.>]<Ч-зв.>)⁺

[(<Б-2560>)*[<Б-сст.>]<Б-зв.>]

Где ()* — повтор 0 или более раз, ()⁺.— повтор 1 или более раз, [] — включение 1 или 0 раз.

Для приведенного ранее примера: 0, 3, 556, 10... алгоритм сформирует следующий код: <Б-0><Ч-3><Б-512><Б-44><Ч-10>, или, согласно таблице, 001101011001100101001011010000100 (разные коды в потоке выделены для удобства). Этот код обладает свойством префиксных кодов и легко может быть свернут обратно в последовательность длин серий. Легко подсчитать, что для приведенной строки в 569 бит мы получили код длиной в 33 бита, т.е. коэффициент сжатия составляет примерно 17 раз.

Усредняющий фильтр

Усредняющий фильтр 'average'  Усредняющий фильтр относится к классу фильтров низких частот. Он может использоваться для уменьшения влияния шума на изображение, однако его применение приводит к размытию изображения и ухудшению его четкости. Каждый элемент маски такого фильтра равен 1 /(m*n), где ш и п — размеры маски (число строк и столбцов). 

Фильтр average. Синтаксис fspecial ('average',[r c]). Прямоугольный усредняющий фильтр размера r×c. Он предназначен для фильтрации высокочастотного шума, и его работа сопровождается размытием изображения. Применение в программе Matlab фильтра average следующий:

I = imread('1.tif');figure, imshow(I);

h = fspecial ('average', [3 3]);

I2 = imfilter (I,h);figure, imshow(I2);

Применение фильтра average к исходному изображению приводит к небольшому размытию растровых точек.

Алгоритм работы усредняющего фильтра заключается в замене значения

яркости в

текущем пикселе на среднюю яркость, вычисленную по его 8 окрестностям,

включая и сам элемент. Этот фильтр является самым простым. К недостаткам

его можно отнести сглаживание ступенчатых и пилообразных функций. Кроме

того пиксели, имеющее существенно отличное значение яркости и являющимися

шумовыми могут вносить значительный вклад в результат обработки.

Реализация фильтра представлена в виде процедуры:

Procedure AverageFilter(Value:Integer);

Данная процедура осуществляет алгоритм усредняющего фильтра

---

применительно к объекту TBitmap. В него предварительно должна быть

загружено изображение (Рис. № 2). Результат работы усредняющего филтра

можно увидеть на рис. № 3. Параметр Value – порог при котором производятся

манипуляции с пикселом.

Procedure TMainForm.AverageFilter;

var

PrevisionLine:pByteArray;

CurrentLine:pByteArray;

NextLine:pByteArray;

I,J:Integer;

Summ:Integer;

begin

if Image1.Picture.Bitmap.PixelFormat = pf8bit then

begin

for I := 0 to Image1.Picture.Bitmap.Height - 1 do

begin

CurrentLine := Image1.Picture.Bitmap.ScanLine[I];

for J := 0 to Image1.Picture.Bitmap.Width - 1 do

begin

Summ := 0;

if I > 0 then

begin

PrevisionLine := Image1.Picture.Bitmap.ScanLine[I - 1];

if J > 0 then

begin

Summ := Summ + PrevisionLine^[J - 1];

end;

Summ := Summ + PrevisionLine^[J];

if J + 1 < Image1.Picture.Bitmap.Width then

begin

Summ := Summ + PrevisionLine^[J + 1];

end;

end;

if J > 0 then

begin

Summ := Summ + CurrentLine^[J - 1];

end;

Summ := Summ + CurrentLine^[J];

if J + 1 < Image1.Picture.Bitmap.Width then

begin

Summ := Summ + CurrentLine^[J + 1];

end;

if I + 1 < Image1.Picture.Bitmap.Height then

begin

NextLine := Image1.Picture.Bitmap.ScanLine[I + 1];

if J > 0 then

begin

Summ := Summ + NextLine^[J - 1];

end;

Summ := Summ + NextLine^[J];

if J + 1 < Image1.Picture.Bitmap.Width then

begin

Summ := Summ + NextLine^[J + 1];

end;

end;

if (Summ div 9) <= Value then

CurrentLine^[J] := Summ div 9;

end;

end;

Image1.Visible := False;

Image1.Visible := True;

N4.Enabled := True;

end

else

MessageBox(Handle,'Такой формат файла пока не подерживается...',

'Слабоват я пока...',MB_OK or MB_ICONSTOP or

MB_APPLMODAL);

end;

Ядерный магнитный резонанс

Я́дерний магні́тний резона́нс (ЯМР) — це явище резонансного поглинання радіочастотних хвиль деякими ядрами атомів, що розміщені у зовнішньому магнітному полі. Найчастіше ЯМР досліди проводять на ядрах атомів водню, тобто на протонах, або на ядрах ізотопу вуглецю ¹³С. На базі ЯМР була розвинута ЯМР-спектроскопія, що дозволяє з великою точністю розрізняти ядра елемента за їхніми властивостями в різному оточенні в молекулі. Ідентифікує структуромінливі сполуки.

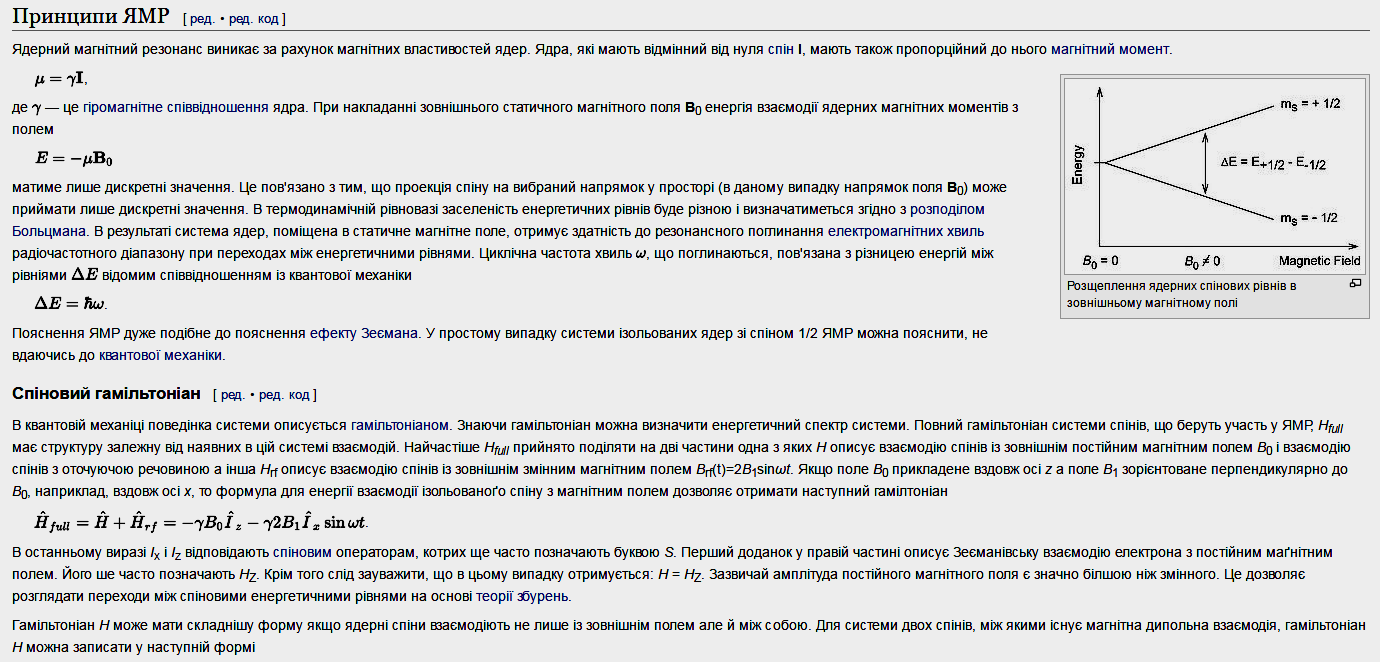
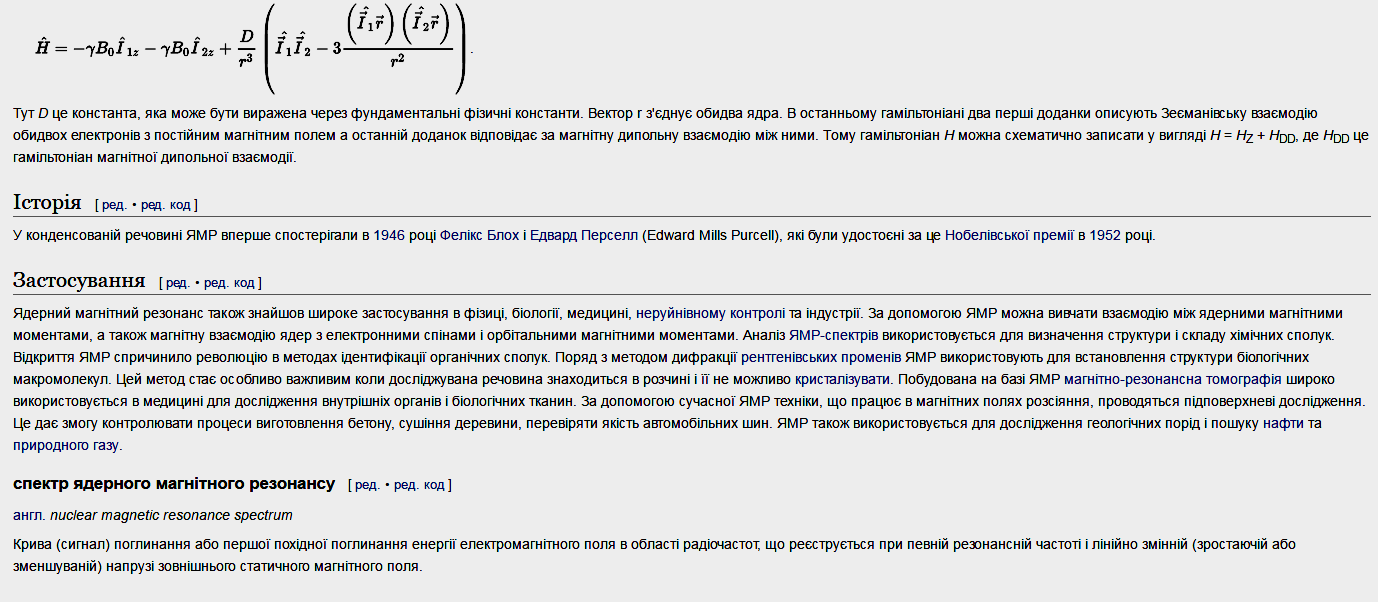
Статистическое распределение спиновых состояний

---

Переобразование Радона

В 1917 году немецкий математик И. Радон [1] предложил метод восстановления (реконструкции) многомерных функций по их интегральным характеристикам, т.е. метод решения обратной задачи интегральной геометрии.

Преобразование Радона - интегральное преобразование функции многих переменных, родственное преобразованию Фурье. Впервые введено в работе австрийского математика Иоганна Радона 1917-го года. Важнейшее свойство преобразования Радона - обратимость, то есть возможность восстанавливать исходную функцию по её преобразованию Радона.

Широкое применение нашёл этот метод в компьютерной томографии [2]:

При просвечивании объекта интенсивность луча на выходе равна интегралу функции распределения плотности вещества вдоль траектории луча. Таким образом, регистрируемое излучение (радоновский образ или проекция), вычисленное под различными углами, позволяет посредством преобразования Радона восстановить изображение поперечного сечения объекта.

Другая широчайшая область применения преобразования Радона и различных его модификаций – цифровая обработка изображений, а именно определение параметров различных кривых и их идентификация, будь то простейшая прямая линия, рукописный шрифт или фотография лица человека.

Рассмотрение преобразования Радона удобно начать с простейшего случая функции двух переменных, к тому же, именно этот случай наиболее практически важен.

Пусть f(x,y) функция двух действительных переменных, определённая на всей плоскости и достаточно быстро убывающая на бесконечности (так, чтобы соответствующие несобственные интегралысходились). Тогда преобразованием Радона функции f(x,y) называется функция

)  

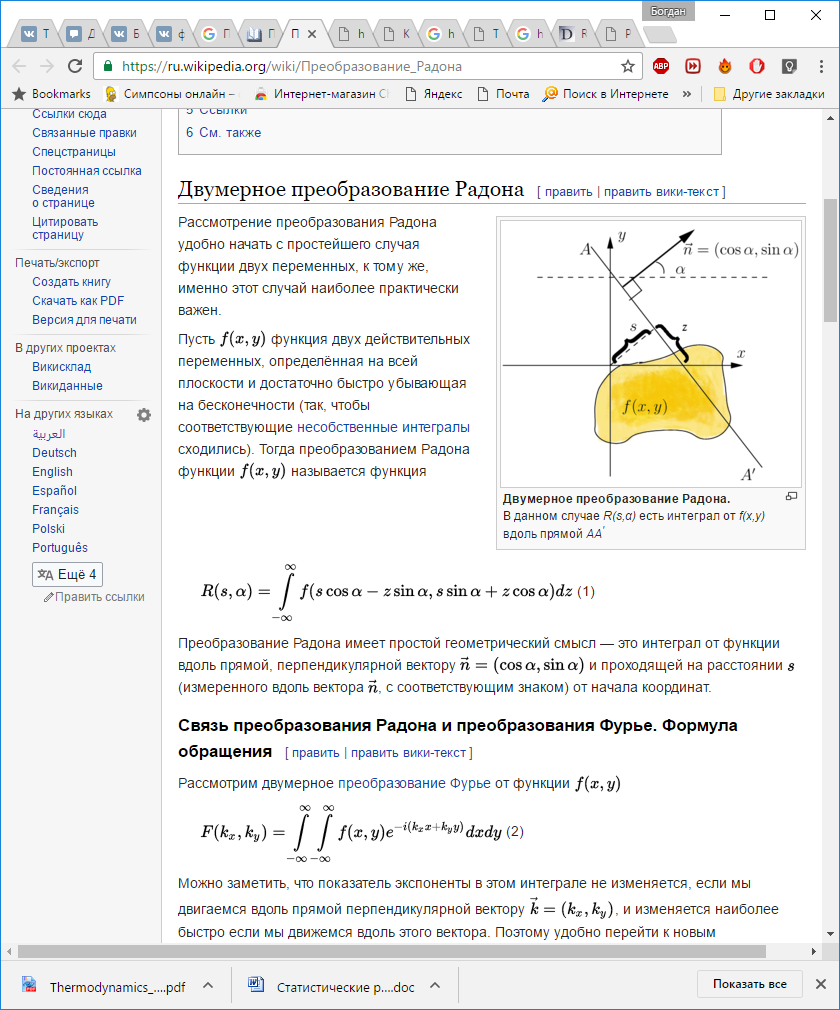
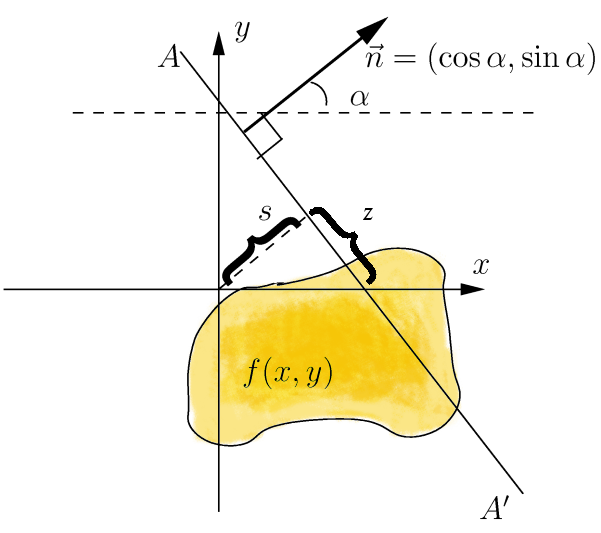
Двумерное преобразование Радона. В данном случае R(s,α) есть интеграл от f(x,y)вдоль прямой AA'

---

Преобразование Радона имеет простой геометрический смысл — это интеграл от функции вдоль прямой, перпендикулярной и проходящей на расстоянии  s (измеренного вдоль вектора , с соответствующим знаком) от начала координат.

В компьютерной рентгеновской томографиилинейка детекторов измеряет поглощение исследуемым объектом параллельного пучка излучения (например, рентгеновских лучей в медицинской томографии, сейсмических волн в геофизической томографии). В соответствии с законом Бугера-Ламберта-Бера интенсивность излучения, измеряемая детектором в точке sлинейки пропорциональна 

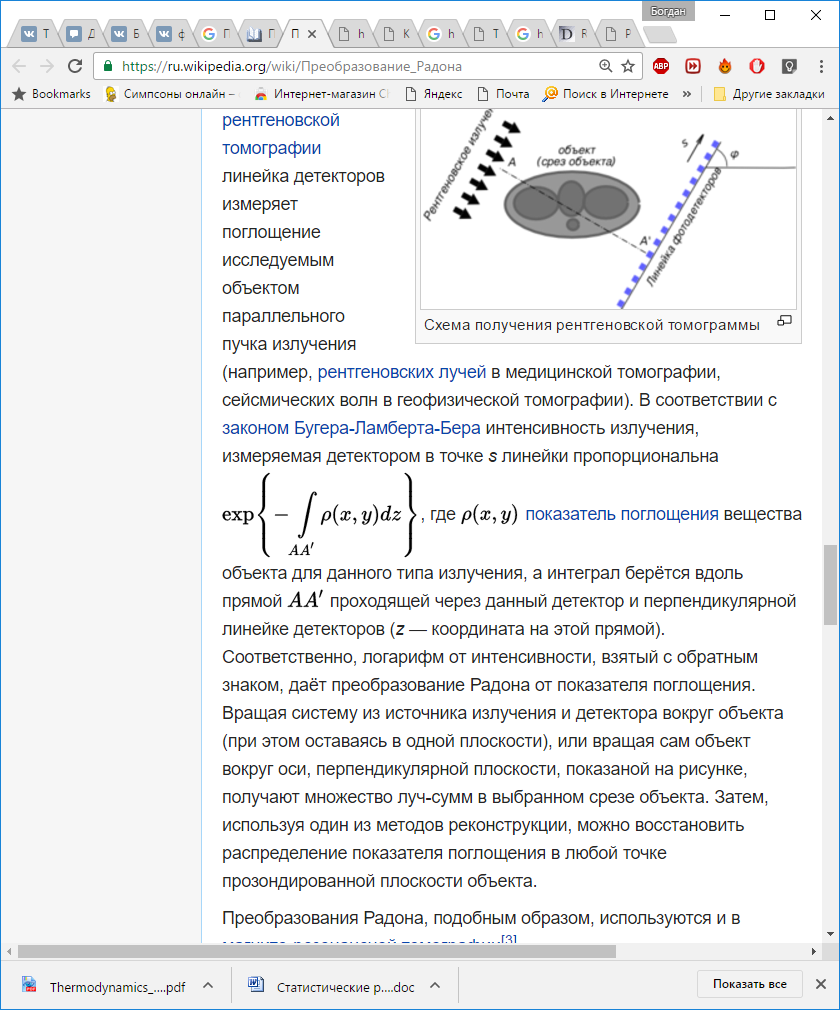
Объекта для излучения, а интеграл берётся вдоль прямой {\displaystyle AA'} проходящей через данный детектор и перпендикулярной линейке детекторов (z — координата на этой прямой). Соответственно, логарифм от интенсивности, взятый с обратным знаком, даёт преобразование Радона от показателя поглощения. Вращая систему из источника излучения и детектора вокруг объекта (при этом оставаясь в одной плоскости), или вращая сам объект вокруг оси, перпендикулярной плоскости, показаной на рисунке, получают множество луч-сумм в выбранном срезе объекта. Затем, используя один из методов реконструкции, можно восстановить распределение показателя поглощения в любой точке прозондированной плоскости объекта.

Преобразования Радона, подобным образом, используются и в магнито-резонансной томографии[3].

Мектод фркатального сжатия

Фрактальная архивация основана на том, что с помощью коэффициентов системы итерируемых функций изображение представляется в более компактной форме. Прежде чем рассматривать процесс архивации, разберем, как IFS строит изображение.

Строго говоря, IFS - это набор трехмерных аффинных преобразований, переводящих одно изображение в другое. Преобразованию подвергаются точки в трехмерном пространстве (x координата, у координата, яркость).

Наиболее наглядно этот процесс продемонстрировал сам Барнсли в своей книге "Фрактальное сжатие изображения". В ней введено понятие Фотокопировальной Машины, состоящей из экрана, на котором изображена исходная картинка, и системы линз, проецирующих изображение на другой экран. Каждая линза проецирует часть исходного изображения. Расставляя линзы и меняя их характеристики, можно управлять получаемым изображением. На линзы накладывается требование они должны уменьшать в размерах проектируемую часть изображения. Кроме того, они могут менять яркость фрагмента и проецируют не круги, а области с произвольной границей.

---