ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.04.2024
Просмотров: 40
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
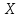 и суточной выработкой продукции
и суточной выработкой продукции 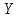 по данным пяти независимых наблюдений представлена в таблице.
по данным пяти независимых наблюдений представлена в таблице.Требуется составить выборочное уравнение линейной парной регрессии
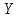 на
на 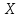 , вычислить коэффициент корреляции
, вычислить коэффициент корреляции 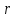 между
между 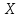 и
и 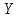 , на уровне значимости
, на уровне значимости  проверить значимость коэффициента корреляции и уравнения регрессии.
проверить значимость коэффициента корреляции и уравнения регрессии. 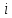 | 1 | 2 | 3 | 4 | 5 |
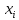 | 3,10 | 3,50 | 4,10 | 4,30 | 4,80 |
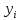 | 2,70 | 3,10 | 3,70 | 4,10 | 4,90 |
Решение.
Найдем выборочные характеристики:
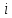 | 1 | 2 | 3 | 4 | 5 | Сумма | Среднее |
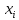 | 3,1 | 3,5 | 4,1 | 4,3 | 4,8 | 19,8 | 3,96 |
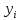 | 2,7 | 3,1 | 3,7 | 4,1 | 4,9 | 18,5 | 3,7 |
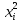 | 9,61 | 12,25 | 16,81 | 18,49 | 23,04 | 80,2 | 16,04 |
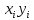 | 8,37 | 10,85 | 15,17 | 17,63 | 23,52 | 75,54 | 15,108 |
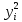 | 7,29 | 9,61 | 13,69 | 16,81 | 24,01 | 71,41 | 14,282 |
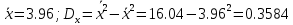
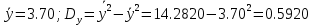
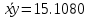
Составим уравнение регрессии
 на
на 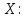
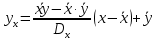
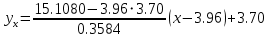
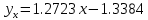
Вычислим коэффициент корреляции
 между
между 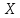 и
и  :
: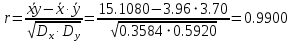
Проверим значимость коэффициента корреляции, то есть проверим гипотезу
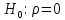 при альтернативной гипотезе
при альтернативной гипотезе 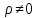 .
.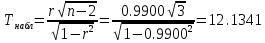
По таблице критических точек распределения Стьюдента по уровню значимости
 и числу степеней свободы
и числу степеней свободы 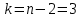 найдем критическую точку двусторонней критической области:
найдем критическую точку двусторонней критической области: 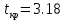 . Так как
. Так как 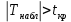 , нулевую гипотезу следует отвергнуть, то есть выборочный коэффициент корреляции статистически значим.
, нулевую гипотезу следует отвергнуть, то есть выборочный коэффициент корреляции статистически значим.Проверим значимость уравнения регрессии в целом. В случае линейной парной регрессии наблюдаемое значение критерия:
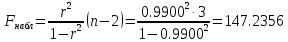
По таблице критических точек распределения Фишера-Снедекора (Приложение 2) по
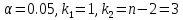 найдем
найдем 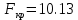 . Так как
. Так как 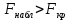 , то на заданном уровне значимости можно утверждать, что полученное уравнение регрессии статистически значимо.
, то на заданном уровне значимости можно утверждать, что полученное уравнение регрессии статистически значимо.Ответ.
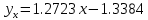
; выборочное уравнение регрессии статистически значимо;
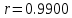 ; выборочный коэффициент корреляции статистически значим.
; выборочный коэффициент корреляции статистически значим.Задача 7.
В таблице приведены данные, отражающие спрос на некоторый товар за семилетний период (усл. ед.). Найти уравнение тренда для временного ряда, полагая тренд линейным.
| Год | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Значение спроса | 43 | 49 | 51 | 59 | 63 | 65 | 71 |
Решение.
Искомое уравнение тренда имеет вид
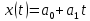 , где коэффициенты
, где коэффициенты 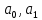 находятся из системы уравнений
находятся из системы уравнений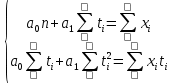
Найдем суммы:
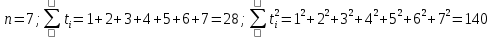
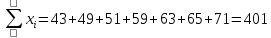
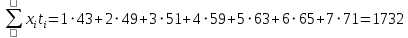
Составим систему:
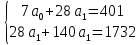
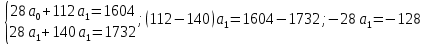
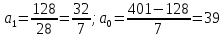
Итак, искомое уравнение тренда:
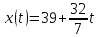
Ответ.
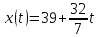 .
.

