Файл: Линейных уравнений называется совместной, если она.doc

	Система линейных уравнений называется совместной, если она: 1) не имеет решений. 2) имеет хотя бы одно решение. 3) множество ее решений пусто. 4) имеет уравнение вида 0х1+0х2+…+0хn=b, b≠0. 5) 1),3).	2
	Вычислить определитель: 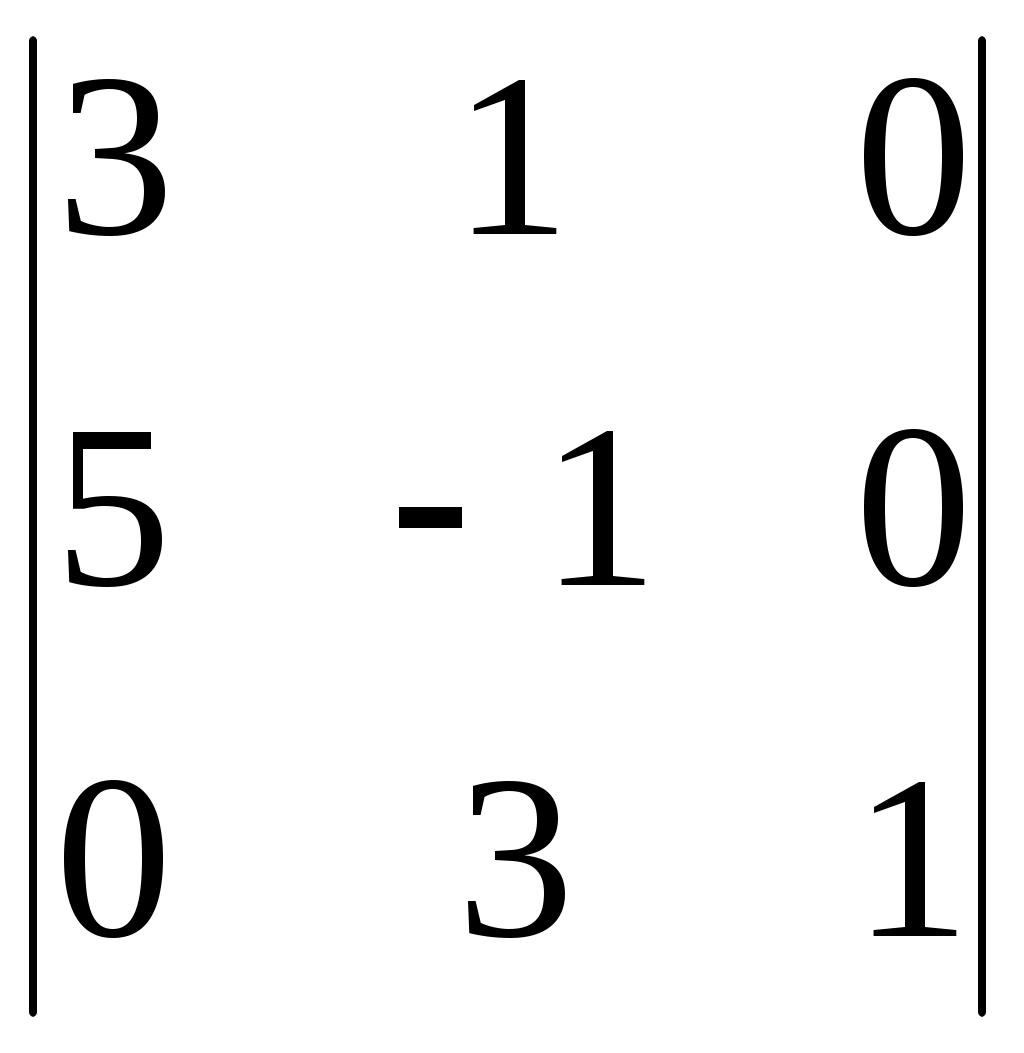24 40 -8 -16 14	3
	Вычислить определитель Δ = 1)12; 2)-12; 3) 6; 4) 2; 5) 16	1
	Найти разность векторов а(-5;2) и в(10;-4) 1) (15;6) 2) (5;-2) 3) (-15;6) 4) (-5;-2) 5) (2;-5)	3
	Даны две точки и в общей декартовой системе координат. Определить координаты вектора : 1) (5;6) 2) (3;-4) 3) (-3;-4) 4) (-5;6) 5) (6;5)	2
	Даны векторы и . Найти скалярное произведение: 21 19 18 -12 15	3
	Алгебраическим дополнением аijназывается число: Aij = (-1)i+j Mij Аij = (-1)j-i Mij Аij = (-1)i-j Mij Аij = (-1)i Mij Аij = (-1)j Mij	1
	Вычислить определитель 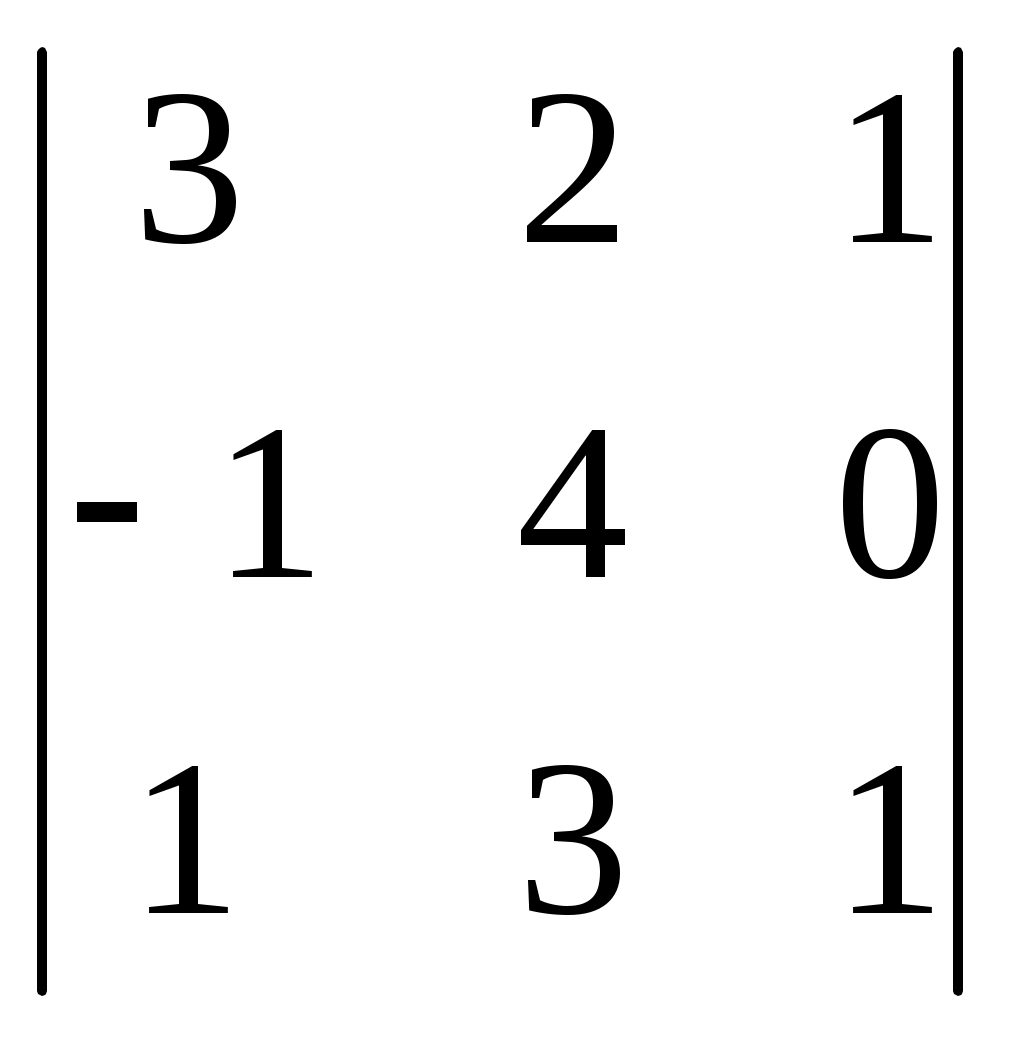: -7 7 -3 5 9	2
	Решить систему уравнений (1;2) (1;1) (-1;1) (2;1) (0;0)	2
	Матрица А-1 называется обратной к матрице А, если А+Е=А-1 А-1 Е=А Е А+А-1 = Е А-1А=АА-1=Е А-1 А = А А-1 Е	4
	При транспонировании квадратной матрицы, определить: Увеличивается в два раза Уменьшается в два раза Меняет знак Не меняется Не меняет знак	4
	Найти точку пересечения прямых 3х-у-2=0 и 2х+у-3=0 (1;-1) (-1;1) (1;1) (1;0) (-1;2)	3
	Какая из данных точек лежит на прямой 3x-y+2=0 M1(3;5) M2(2;-2) M3(-2;2) M4(-2;-4) M5(0;1)	4
	Система линейных уравнений называется неопределенной, если: Она имеет одно решение. Она имеет хотя бы одно решение. Она не имеет решение. Имеет бесконечное множество решений. Она имеет нулевое решение.	4
	Найдите А Е, если А= , Е= Е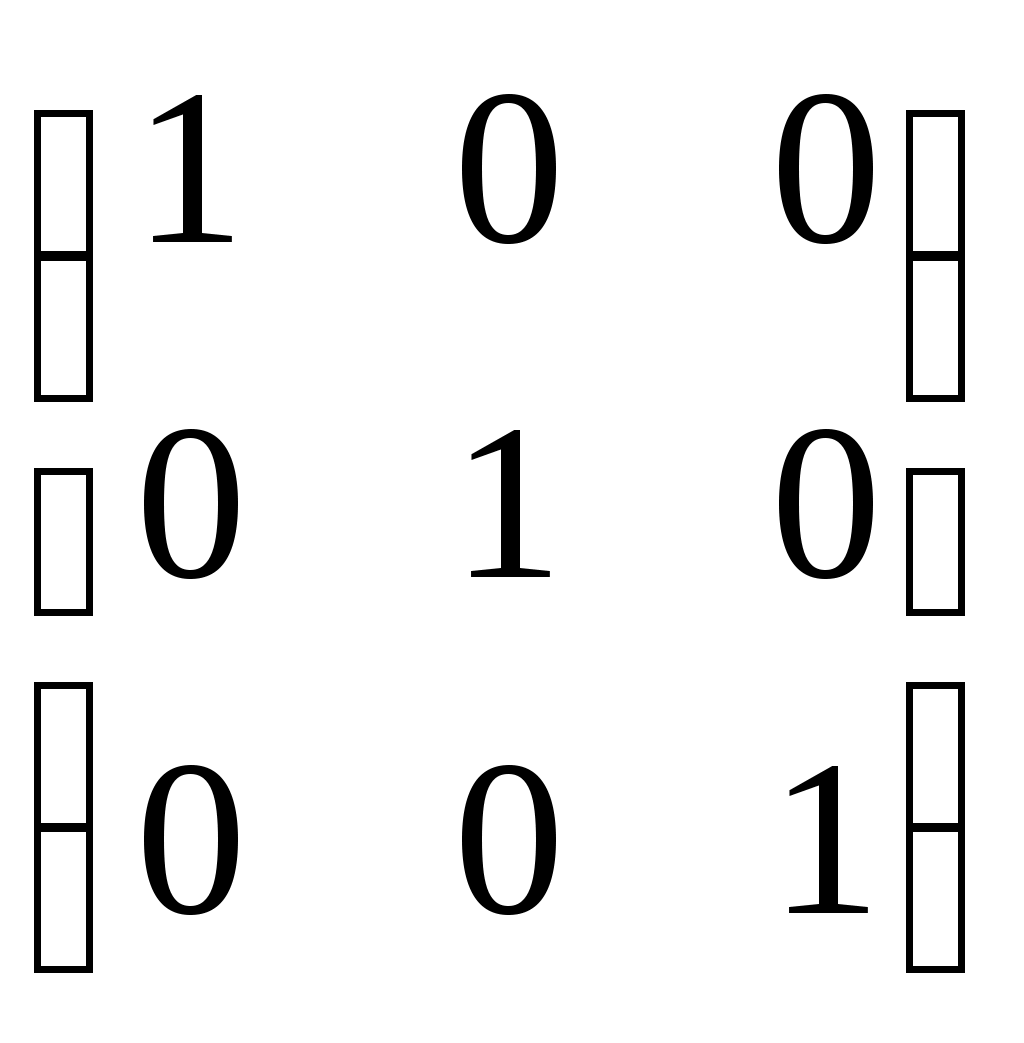 А -А –Е А2	2
	Вычислить определитель : 0 -1 -4 7 1	3
	Алгебраическое дополнение элемента а21 матрицы А= равно… -1 9 -9 10 -2	3
	Дана система уравнений . Укажите правильную матричную запись системы, если A (aij), B(вi), X(xj): BX=A A'X=B A-1X=B AX=B B-1X=A	4
	Матрица называется единичной матрицей, если ... элементы первой строки состоят из одних единиц элементы первого столбца состоят из одних единиц диагональные элементы диагональной матрицы состоят из одних единиц все элементы равны единице является матрицей состоящей из одной строки или из одного столбца.	3
	Вычислите алгебраическое дополнение А32 элемента а32 определителя D= 13; 4; - 4; 6; 0;	3
	Какое условие требуется для сложения двух матриц? Различные размерности. Количество столбцов первой матрицы равно количеству строк второй матрицы. Количество строк первой матрицы равно количеству столбцов второй матрицы. Одинаковые размерности. Диагональные элементы одинаковы.	4
	Выполнить умножение матриц АВ, где А= , В=	1
	Система линейных уравнений, имеющая хотя бы одно решение называется … совместной несовместной однородной независимой нет правильного ответа	1
	Определитель треугольной матрицы равен… 0 произведению элементов побочной диагонали 1 равен произведению элементов главной диагонали .обратной матрице	4
	Найти определитель 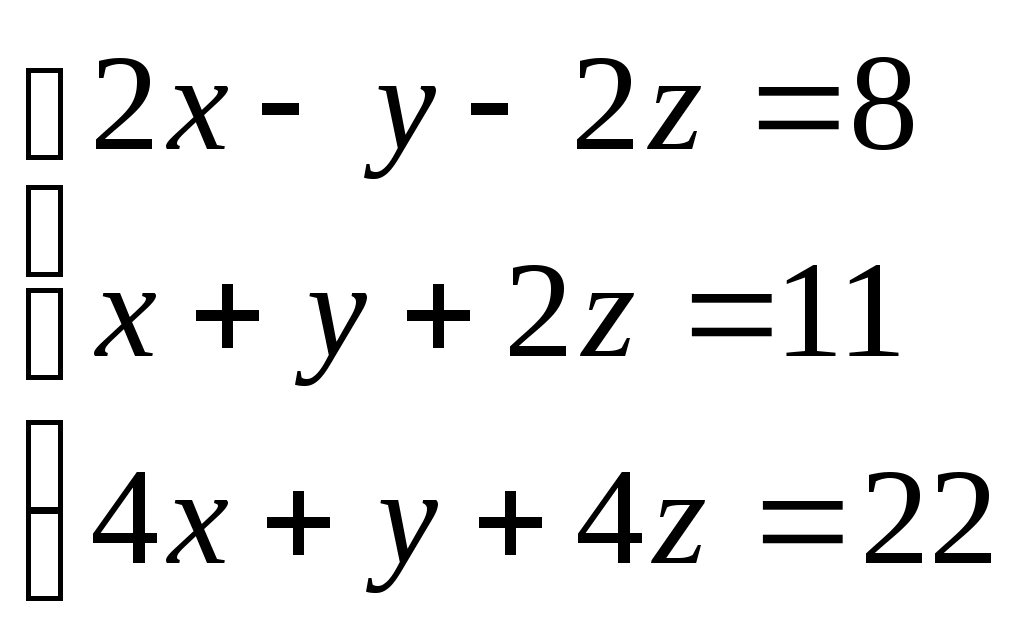системы = 8 = 6 = -8 = 4 = 1	2
	Какое из следующих утверждений ложно? A) А × А –1 = А-1 × А = Е ; B) если а11 а22 – а 12 а21¹ 0 ,то существует обратная матрица А-1; C) если а11а22 – а12а21 = 0 , то для А найдется обратная ей матрица А-1. D) А= 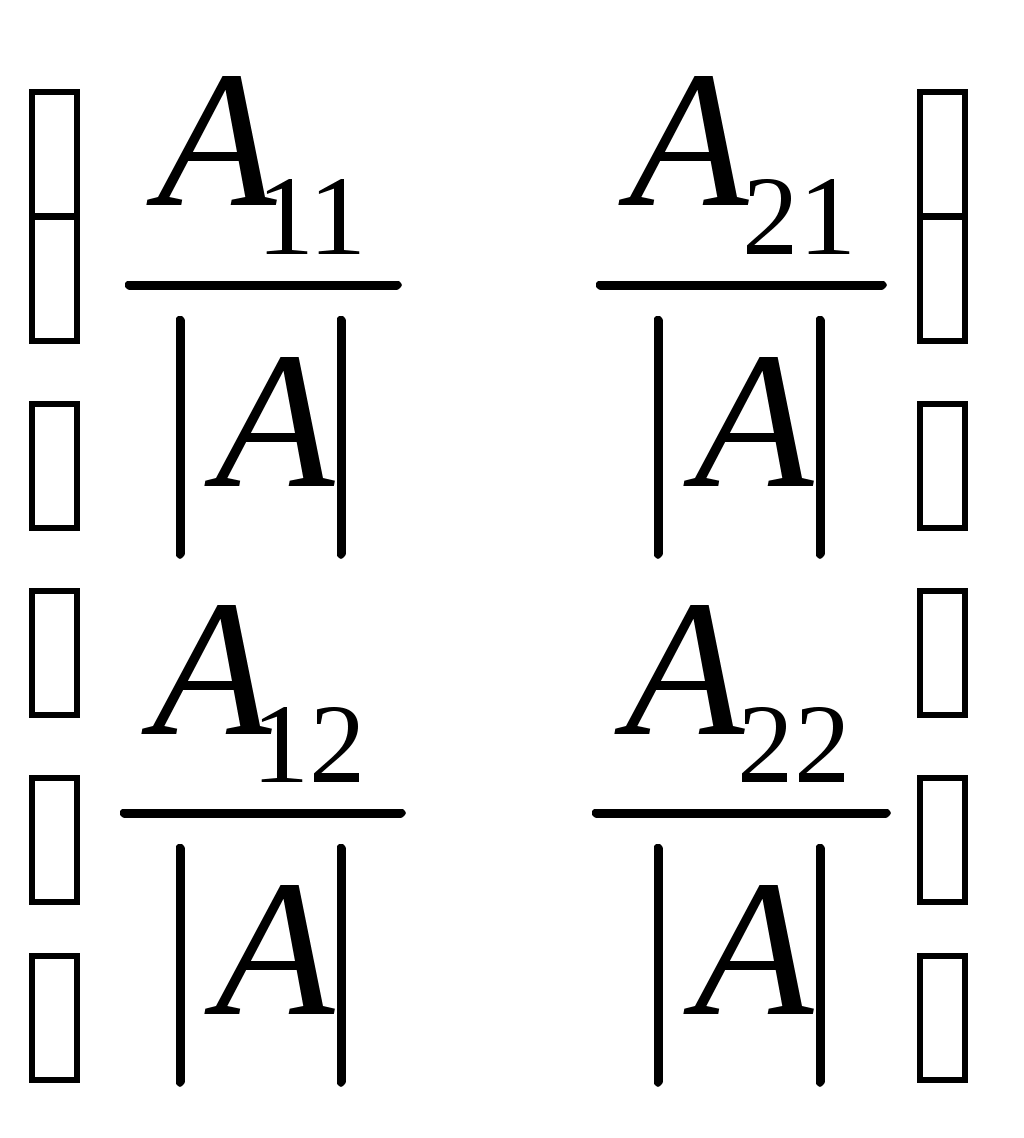; E) А-1 ×Е =А-1.	3
	В каких случаях применяется метод Крамера решения совместной системы неоднородных линейных уравнений ? 1) Если определитель основной матрицы отличен от нуля; 2) Если ранг r основной матрицы не равен числу неизвестных n (r¹n); 3) Если r 4) Если r>n. 5) Если число линейно независимых строк основной матрицы равен рангу расширенной матрицы.	1
	Определить расстояние между точками А (3,8) и В (-5, 14): 1) 5. 2) 10. 3) . 4)-10. 5) 13.	2
	Матрица называется квадратной n-го порядка 1) если число ее строк равно числу столбцов 2) если она состоит из одной строки 3) если она состоит из двух столбцов 4) если она содержит две одинаковые строки 5) если количество строк m, а столбцов n	1
	Определитель матрицы не изменится 1) если умножить его на 0 2) если к элементам, какой либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и тоже число 3) если элементы строки поменять местами 4) если строки поменять местами 5) если столбцы поменять местами	2
	Если квадратная матрица содержит две одинаковые строки (столбцы), то ее определитель равен 1) определитель = - определитель 2) 0 3) 5 4) теряет смысл 5) ничего не изменится	2
	Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 1) 1 2) 0 3) ничему 4) бесконечности 5) 5	2
	Алгебраическим дополнением Аij элемента аij матрицы n-го порядка наз-ся 1) Его минор взятый со знаком (-1)(i+j): Aij=(-1)(i+j)*Mij 2) его определитель вычисленный по формуле Сарруса 3) число порядка искомой матрицы 4) порядок матрицы плюс все элементы по глав. диагонали 5) один элемент аij	1
	Минором Mij элемента аij матрицы n-ого порядка называется 1) Определитель этой матрицы, вычисляемый по формуле треугольника 2) определитель матрицы (n-1)-го порядка, полученной из матрицы А вычёркиванием i-й строки и j-го столбца 3) Dеl матрицы расписанный по элементам строки 4) определитель меньшего порядка 5) число элементов по главной диагонали	2

---

---

5

---

Какое из следующих утверждений ложно?

1) А  А ^–1 = А^-1  А = Е ;

2) если а₁₁ а₂₂ – а ₁₂ а₂₁ 0 ,то существует обратная матрица А^-1;

3) если а₁₁а₂₂ – а₁₂а₂₁ = 0 , то для А найдется обратная ей матрица А^-1.

4) А= ;

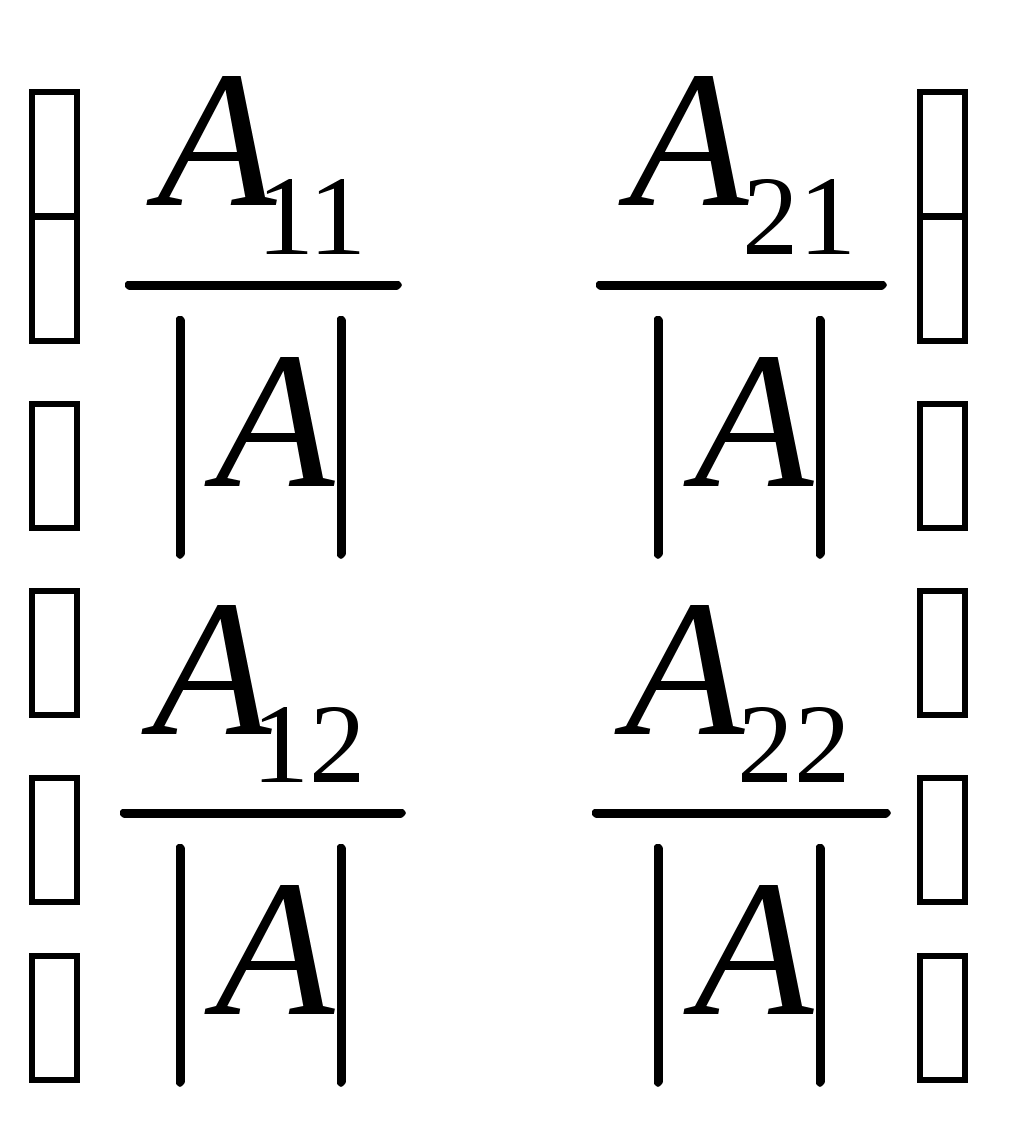5) А^-1Е =А^-1.

---

5

---