Файл: Лабораторная работа 1 по курсу Специальные разделы теории управления Проверил СанктПетербург 2023.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 19
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Санкт-Петербургский государственный университет
информационных технологий, механики и оптики
Кафедра систем управления и информатики
Лабораторная работа № 1
по курсу «Специальные разделы теории управления»
Выполнил:
Проверил:
Санкт-Петербург
2023
Содержание
Цель работы 3
Исходные данные 3
Выполнение работы 4
Вывод 9
Цель работы
Ознакомление с работой экстраполятора нулевого порядка и основными приемами моделирования линейных дискретных систем в пакете прикладных программ SIMULINK.
Исходные данные
Схема моделирования представлена на Рисунке 1.

Рисунок 1 – Схема моделирования
В соответствии с вариантом даны следующие значения параметров объекта управления и интервала квантования:
T = 0.4 c (1)

Выполнение работы
С учетом (1), реализованная в прикладном пакете SIMULINK схема
принимает вид (Рисунок 2)
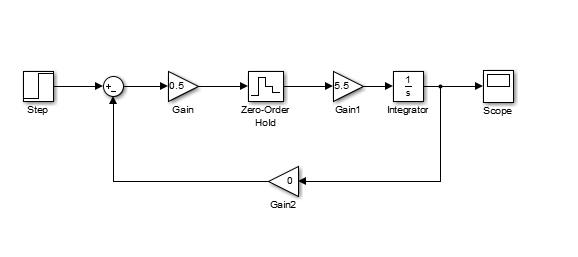
Рисунок 2 – Схема моделирования в SIMULINK
1. Экспериментальное определение коэффициентов
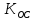 , соответствующим границам устойчивости
, соответствующим границам устойчивостиИз [1] известно, что дискретные системы могут иметь 3 типа границ устойчивости:
Нейтрального типа;
Колебательная;
Результаты эксперимента
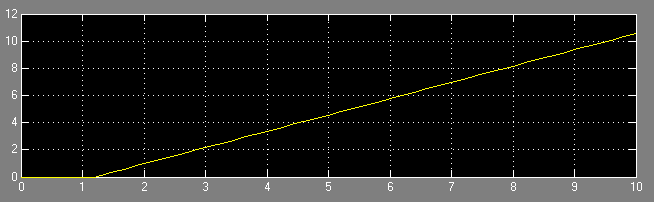
Рисунок 3 – Иллюстрация переходного процесса при
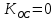
Из Рисунка 3 видно, что это граница устойчивости нейтрального типа.
На Рисунке 4 получили колебательную границу устойчивости.
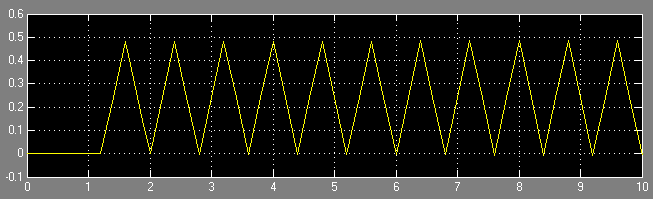
Рисунок 4- Иллюстрация переходного процесса при
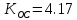
2. Влияние ЭНП на устойчивость замкнутой системы
Из Рисунка 4 при значениях
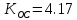
система находится на колебательной границе устойчивости. При увеличении параметра ЭНП – шага дискретизации, система становится неустойчивой (см. Рисунок 5).

H(t)
t t

Рисунок 5 – Иллюстрация переходного процесса при T = 0.6 c
При уменьшении – колебательность процесса снижается.
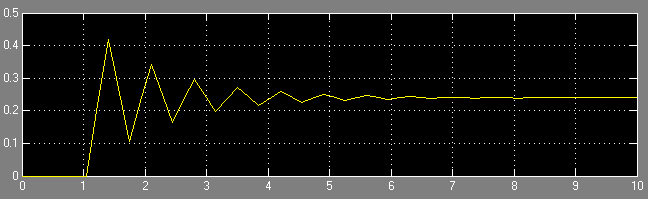
Рисунок 6 – Иллюстрация переходного процесса при T = 0.35 c
3. Представление переходных процессов для случая б
См. пункт б.
4. Анализ влияния МЛСОС на колебательность процесса
Увеличение МЛСОС приводит к повышению колебательности, вплоть до разноса системы (см. Рисунок 7).

Рисунок 7 – Иллюстрация переходного процесса при МЛСОС = 0.6
Уменьшение - уменьшению колебательности (см Рисунок 8).
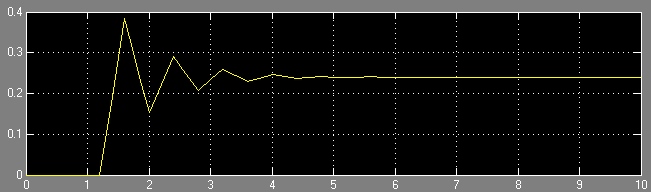
Рисунок 8 – Иллюстрация переходного процесса при МЛСОС = 0.4
5.
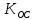 , при которых наблюдается максимальная колебательность и отсутствуют колебания
, при которых наблюдается максимальная колебательность и отсутствуют колебанияМаксимальная колебательность будет наблюдаться при
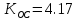
(см. пункт б, Рисунок 4).
Отсутствовать колебательность будет при
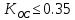
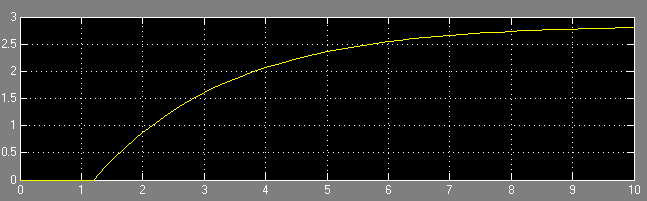
Рисунок 9- Иллюстрация переходного процесса при
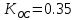
6. Привести переходные характеристики для случая е
см. пункт е.
7. Привести значения коэффициента обратной связи и переходные характеристики, соответствующие:
затухающему процессу без колебаний от интервала к интервалу дискретности.
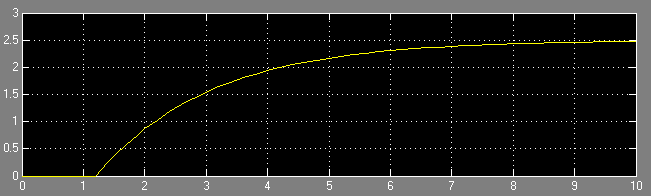
Рисунок 10 - Иллюстрация переходного процесса при
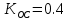
расходящемуся процессу без колебаний от интервала к интервалу дискретности

Рисунок 11 - Иллюстрация переходного процесса при
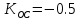
незатухающему процессу с колебаниями от интервала дискретности к интервалу дискретности
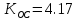 (см. пункт б, Рисунок 4).
(см. пункт б, Рисунок 4).затухающему процессу с колебаниями от интервала дискретности к интервалу дискретности
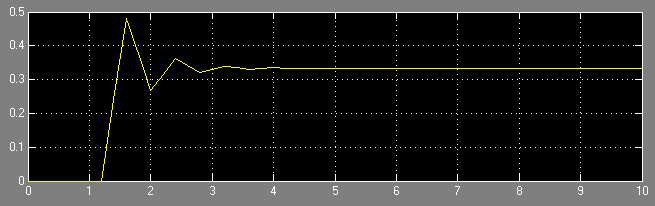
Рисунок 12 - Иллюстрация переходного процесса при
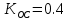
расходящемуся процессу с колебаниями от интервала дискретности к интервалу дискретности
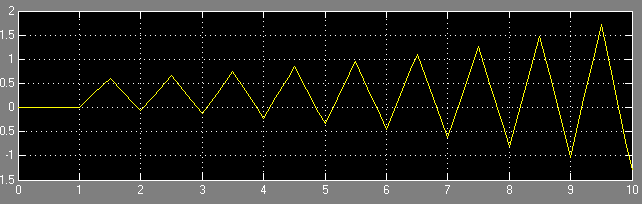
Рисунок 13 - Иллюстрация переходного процесса при
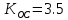
8. Определить экспериментальным образом
 , соответствующий оптимальному по быстродействию переходному процессу
, соответствующий оптимальному по быстродействию переходному процессу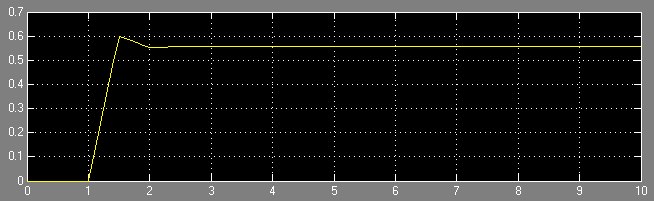
Рисунок 14 - Иллюстрация переходного процесса при
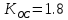
Вывод
В ходе работы было установлено, что изменение
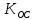 и параметров ЭНП влияет на уровень колебательности и устойчивость системы.
и параметров ЭНП влияет на уровень колебательности и устойчивость системы.
