Файл: Учреждение высшего образования алтайский государственный аграрный университет.docx
Добавлен: 03.05.2024
Просмотров: 33
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«АЛТАЙСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ»
В.А. Садовая, А.А. Смышляев
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Рабочая тетрадь по дисциплине
«Начертательная геометрия и инженерная графика»
для студентов инженерного факультета
Студентагруппы
________________________
(ф.и.о.)
БАРНАУЛ 2019
Рецензент:
Старший преподаватель кафедры «Механика и инженерная графика» Алтайского ГАУ И.Л. Новожилов.
Садовая, В.А. Начертательная геометрия: рабочая тетрадь по дисциплине «Начертательная геометрия и инженерная графика» (раздел «Начертательная геометрия») для студентов инженерного факультета по направлениям: 35.03.06 «Агроинженерия» и 23.03.03 «Эксплуатация транспортно-технологических машин и комплексов» – Барнаул: РИО Алтайского ГАУ, 2019. – 39 с.
Издание для практических занятий по дисциплине «Начертательная геометрия и инженерная графика» (раздел «Начертательная геометрия») содержит указания к изучению тем начертательной геометрии, перечень принятых обозначений; указание перечня основной литературы, набор задач по каждой теме дисциплины, список вопросов для самопроверки, примерные вопросы к экзамену и и пример экзаменационного билета.
Учебное издание одобрено методической комиссией инженерного факультета (протокол № 10 от 29 июня 2019 г.) и рекомендовано к печати.
Печатается по решению кафедры «Механика и инженерная графика»
(протокол № 10 от 27 июня 2019 г.).
Садовая В.А., Смышляев А.А., 2019
Кафедра «Механика и инженерная графика», 2019
ФГБОУ ВО Алтайский ГАУ, 2019
Содержание
Введение…………………………………………………………………… 4
ТЕМА 1. ТОЧКА И ПРЯМАЯ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ…… 5
ТЕМА 2. Плоскость………………………………………………………… 9
ТЕМА 3. поверхности. ТОЧКа и линия на поверхности……… 12
ТЕМА 4. Позиционные задачи………………………………………… 15
ТЕМА 5. Метрические задачи………………………………………… 22
ТЕМА 6. Преобразование чертежа способом замены
плоскостей проекций……………………………………… 24
ТЕМА 7. Преобразование чертежа способом
плоско - параллельного движения и вращением
вокруг оси, перпендикулярной одной
из плоскостей проекций…………….…………………… 26
ТЕМА 8. Развертывание поверхностей…………………………… 28
Вопросы для самопроверки и примерные к экзамену 32
Пример экзаменационного билета……………………………………………… 35
Библиографический список…………………………………………… 37
Введение
Начертательная геометрия является одним из разделов геометрии, в котором пространственные фигуры, представляющие совокупность точек, линий и поверхностей, изучаются по их проекционным отображениям.
Одной из основных задач начертательной геометрии является создание метода отображения трехмерных фигур на плоскости и разработка способов решения позиционных и метрических задач, связанных с этими фигурами, по их плоскостным отображениям.
При изучении курса «Инженерная графика» большое значение придается решению задач и выполнению упражнений, что помогает закрепить знания, полученные при изучении теоретического материала, и развивает пространственное воображение.
Предлагаемая рабочая тетрадь разработана для аудиторных занятий и самостоятельной домашней работы. Часть задач, по указанию преподавателя, решается в аудитории во время практических занятий, остальные – самостоятельно.
Перед практическими занятиями необходимо проработать теоретический материал по соответствующей теме.
Задачи решаются непосредственно в рабочей тетради. Все построения выполняются только с помощью чертежных инструментов, карандашом, причем следует выдерживать требуемую по ГОСТу толщину линий и шрифта.
Приняты следующие обозначения:
а) Точки и их проекции обозначаются прописными буквами латинского алфавита и цифрами;
Например: А (А, А); 1 (1,1)
б) Линии обозначаются строчными буквами латинского алфавита;
Например: а (а, а); m (m, m)
в) Плоскости обозначаются строчными буквами греческого алфавита;
Например: (V, H); (V, H)
г) Поверхности обозначаются строчными буквами греческого алфавита;
Например: q
д) Углы обозначаются строчными буквами греческого алфавита;
Например: α°
Графические знаки – символы:
- параллельность,
- результат совпадения,
- пересечение,
- перпендикулярность,
• - скрещивающиеся прямые,
, - принадлежность.
ТЕМА 1. ТОЧКА И ПРЯМАЯ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ
1.1. Даны координаты точек А (15,30,20); В (35,20,10). Построить проекции этих точек и их наглядные изображения.
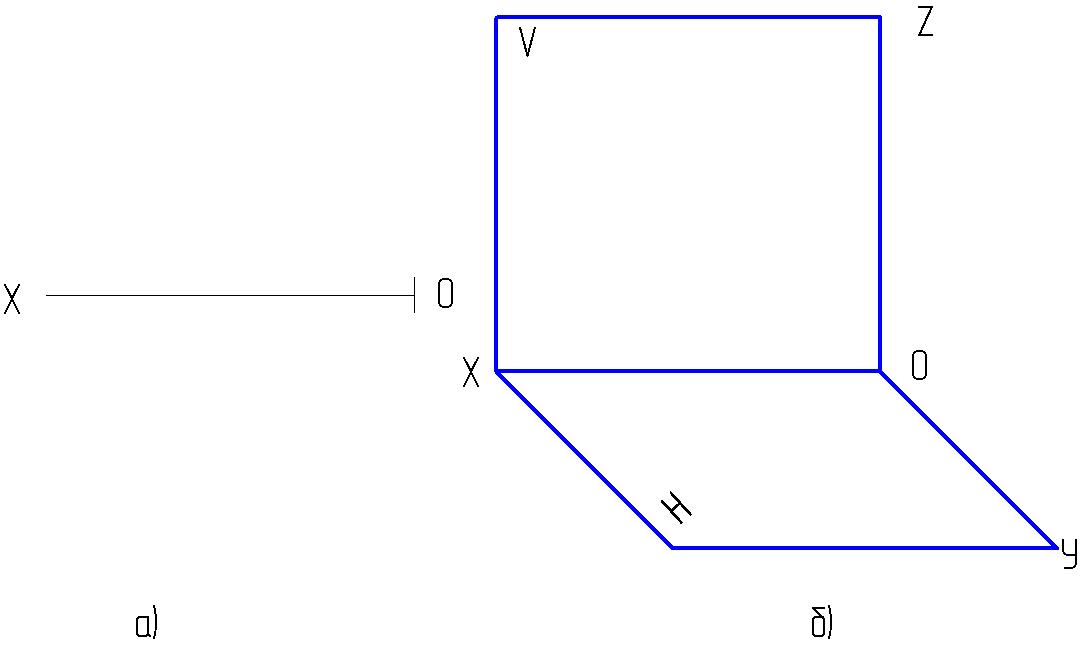
1.2. Определить координаты точек А и В. Построить проекции точек.
А( , , ) ; В( , , )
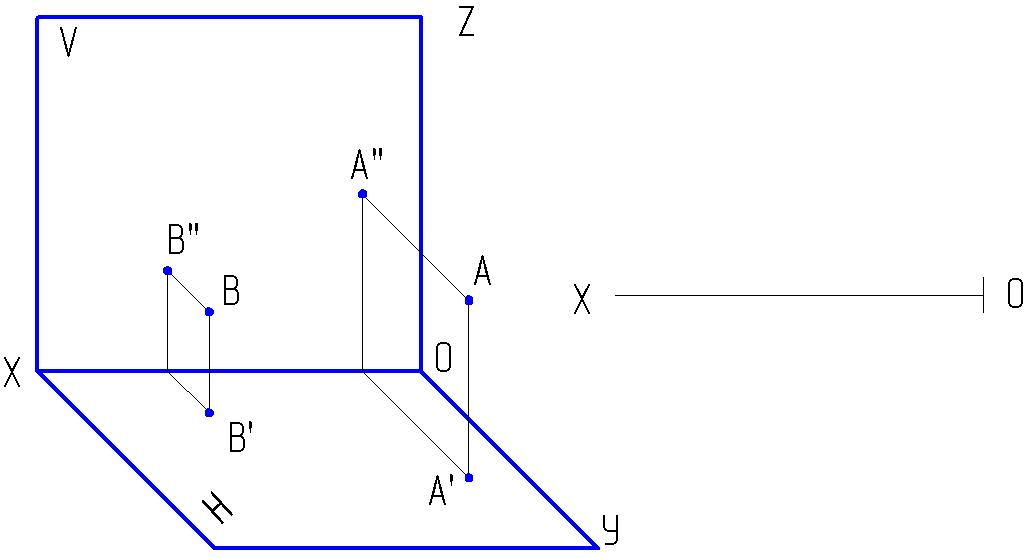
1.3. По двум проекциям точек А, В, С построить третьи проекции и их наглядные изображения. Определить координаты точек:
А ( , , ); В ( , , ); С ( , , ).
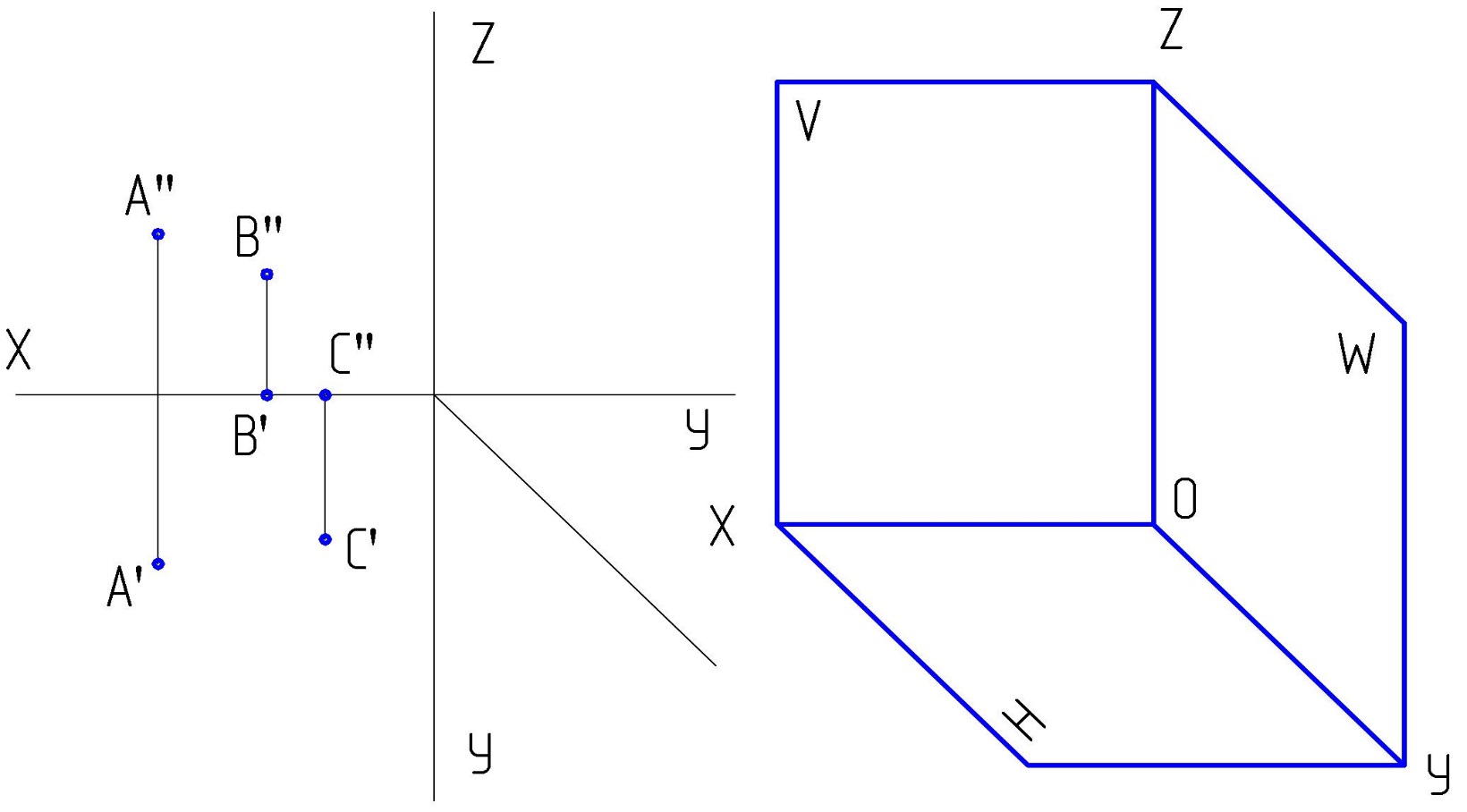
1.4. По заданным координатам точек построить проекции прямой АВ и её следы.
А (65, 20, 5) и В (45, 10, 20).
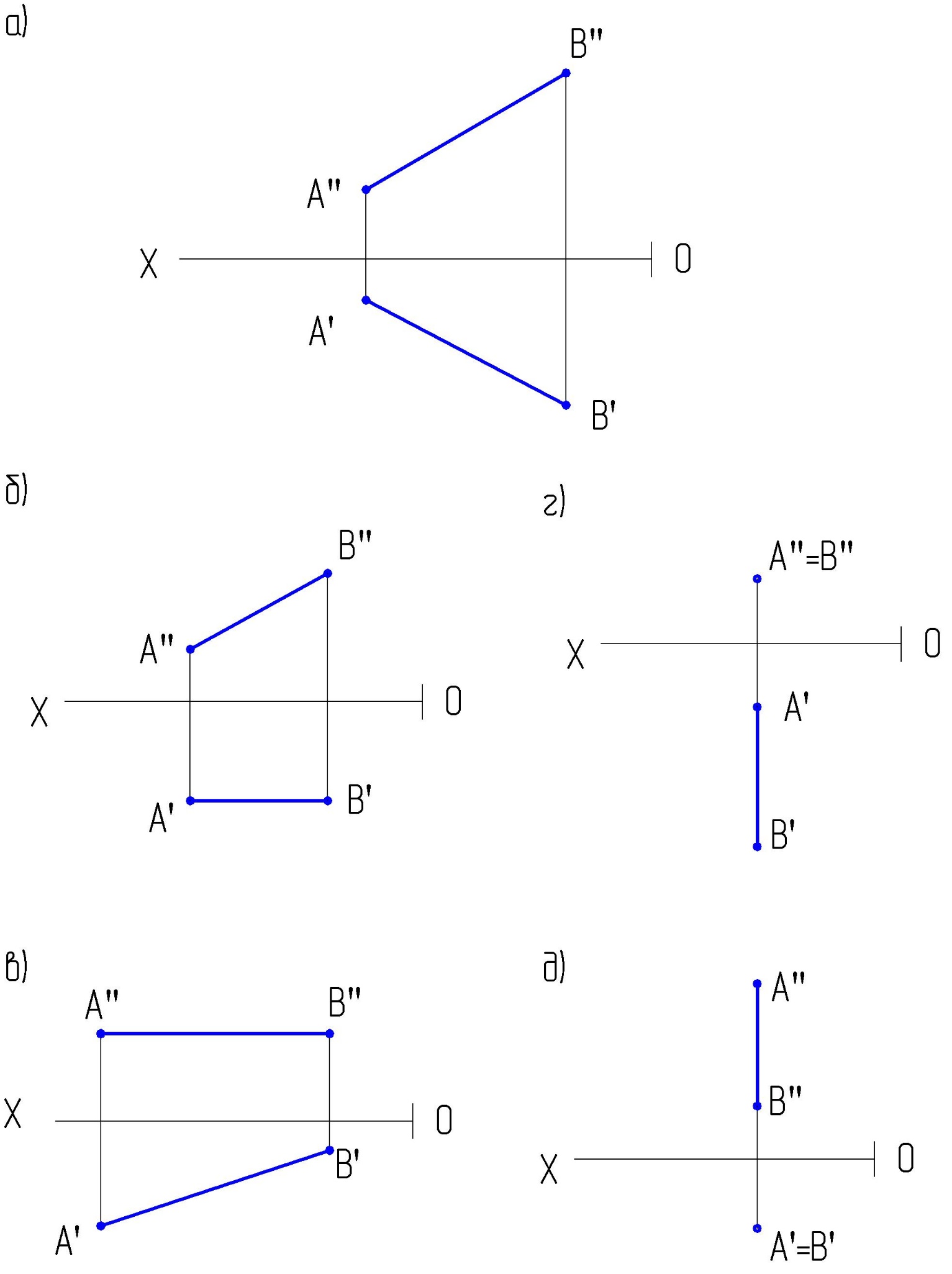
1.5. Определить натуральную величину отрезка АВ и углы наклонов отрезка
к фронтальной и горизонтальной плоскостям проекций.
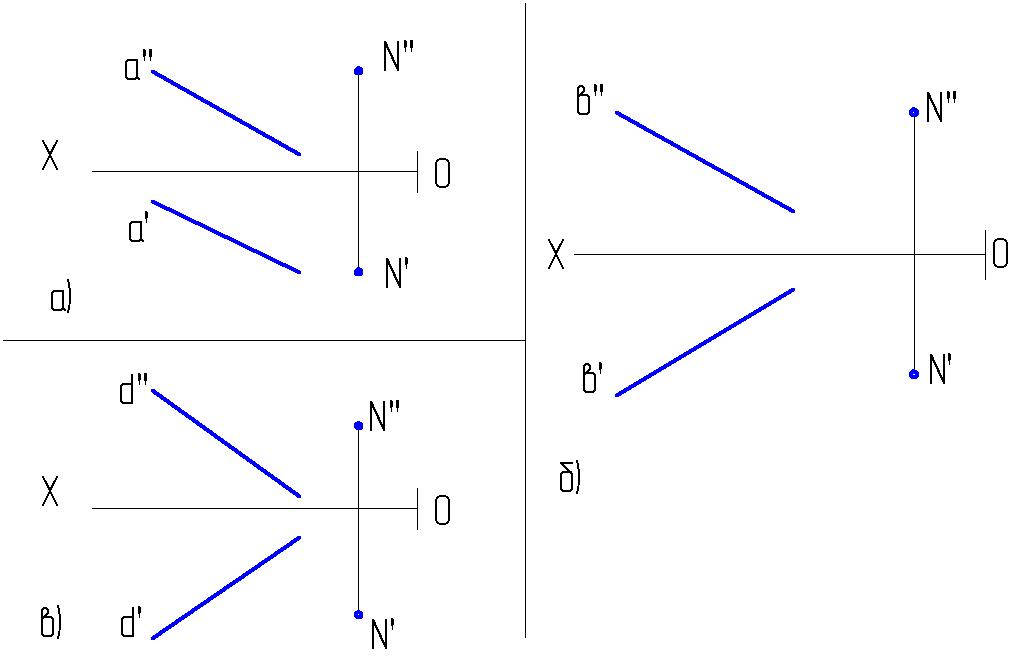
1.6. Через точку N провести прямую l:
а) пересекающую прямую а;
б) параллельную прямой в;
в) скрещивающуюся с прямой d.
ТЕМА 2. Плоскость
2.1. Записать символически: 1. Чем задана плоскость
2. Как она расположена в пространстве
3. Её название
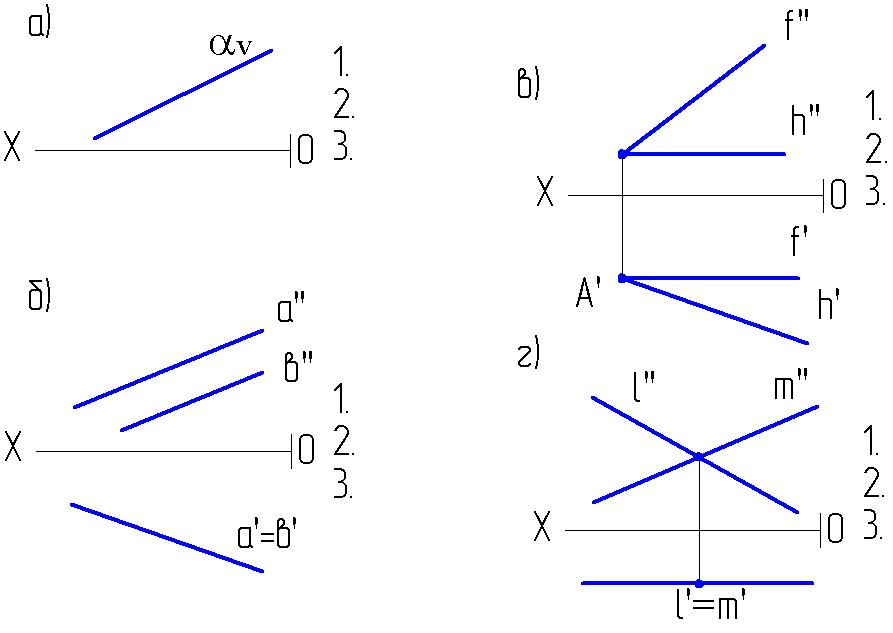
Примечание: если плоскость перпендикулярна какой-либо плоскости проекций, то всё, что в ней лежит, проецируется в одну прямую на эту плоскость проекций (прямо в след этой плоскости).
2.2. Провести в каждой из заданных плоскостей горизонталь на расстоянии 20 мм от горизонтальной плоскости проекций Н и фронталь на расстоянии 25 мм от фронтальной плоскости проекций V.
2.3. Определить недостающие проекции точек М и N, принадлежащих заданным плоскостям.
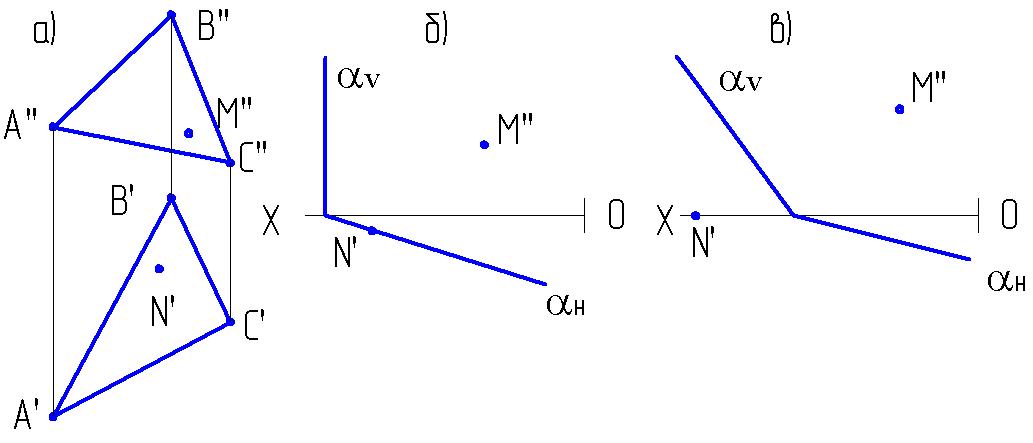
2.4. Заключить прямую l в заданную плоскость:
а) α V б) α Н в) Н
α (l ∩ m) α (αн) (v)
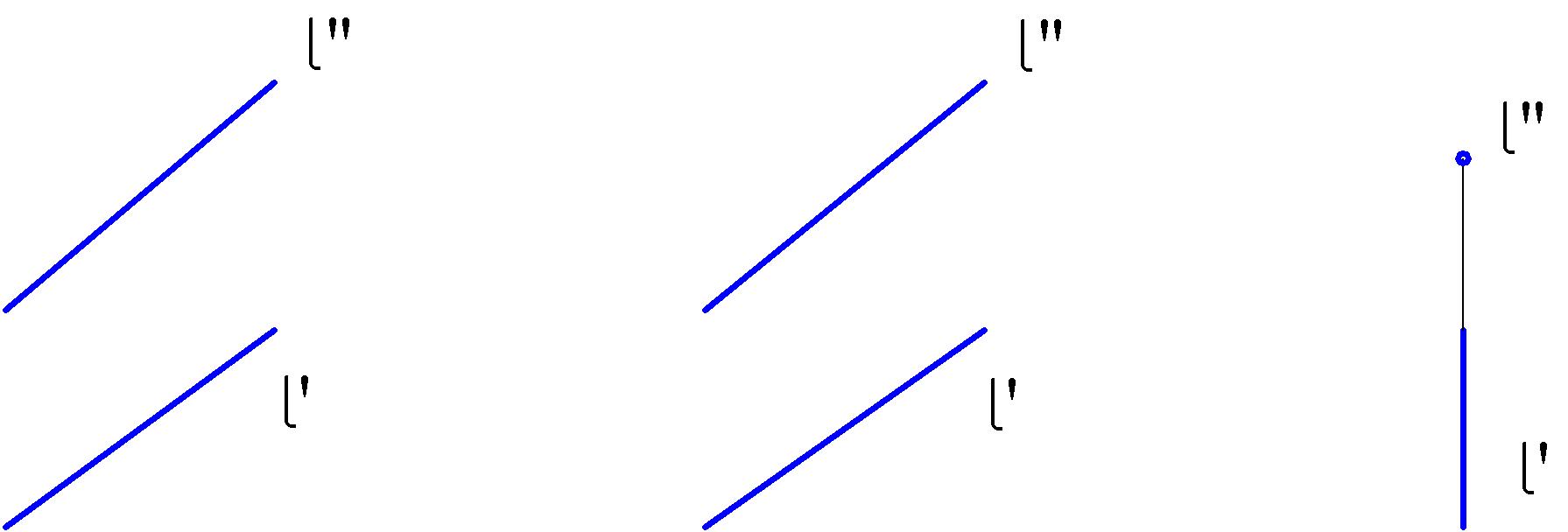
г) V д) γ -плоскость общего положения
(н) γ (l ∩ h)

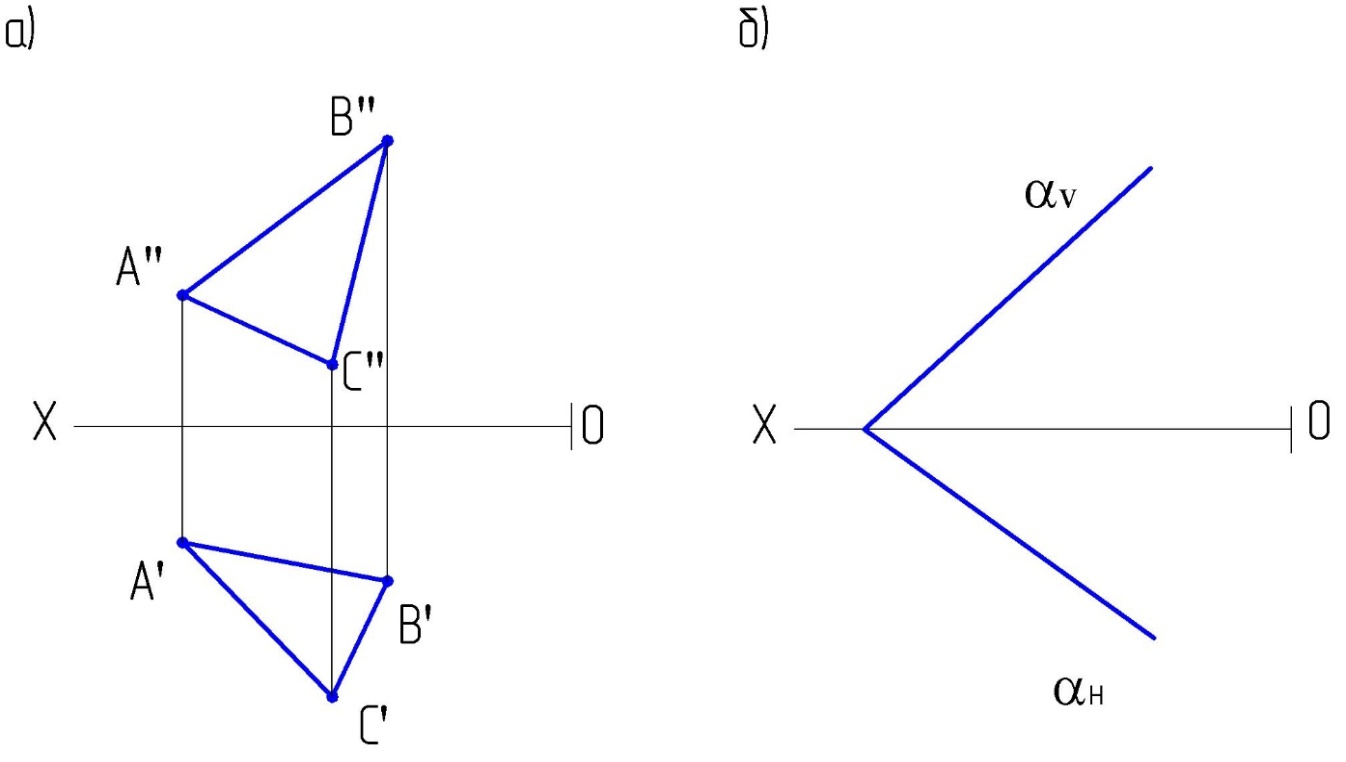
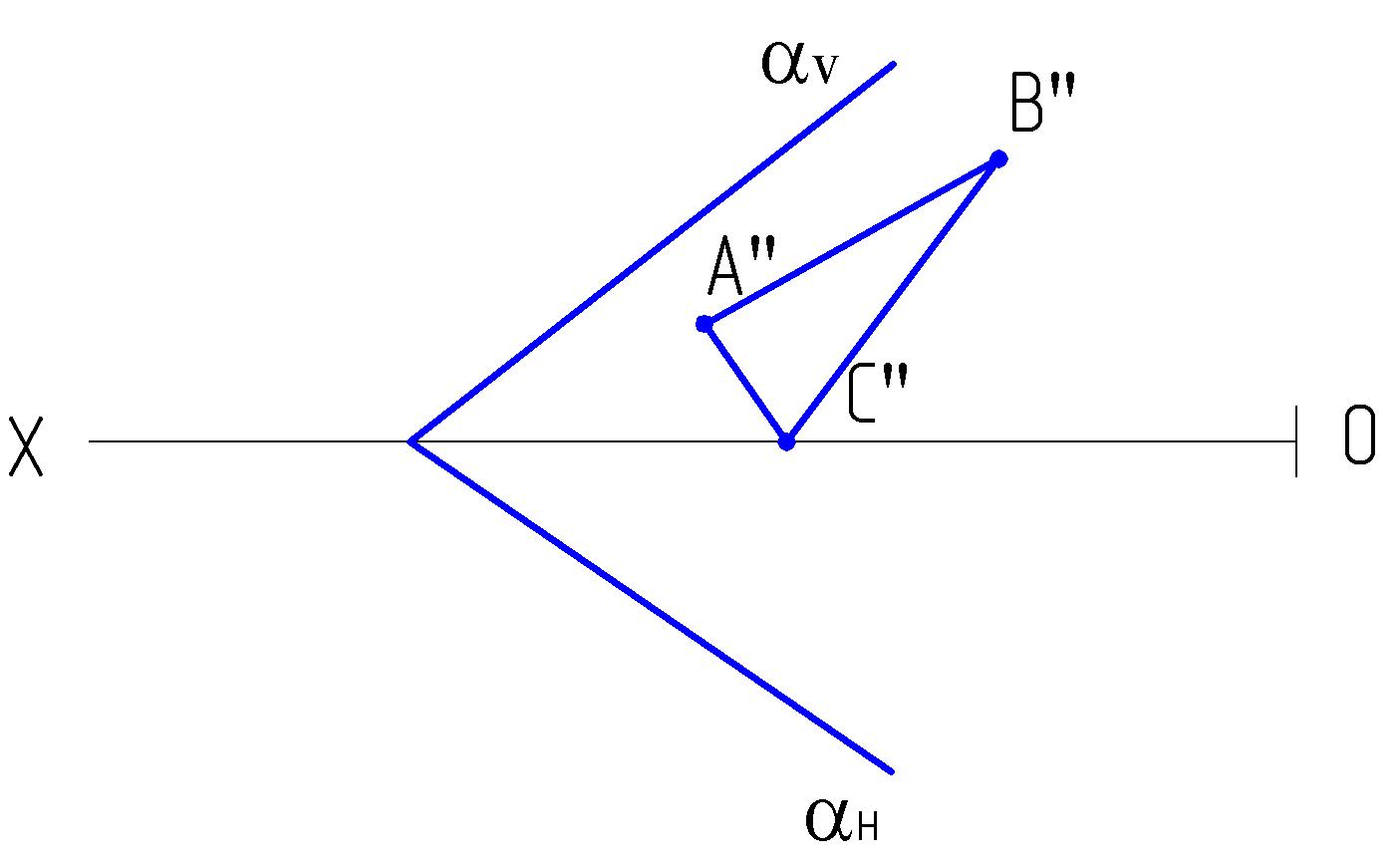
2.5. Построить горизонтальную проекцию треугольника АВС, расположенного в плоскости, заданной:
а) параллельными прямыми;
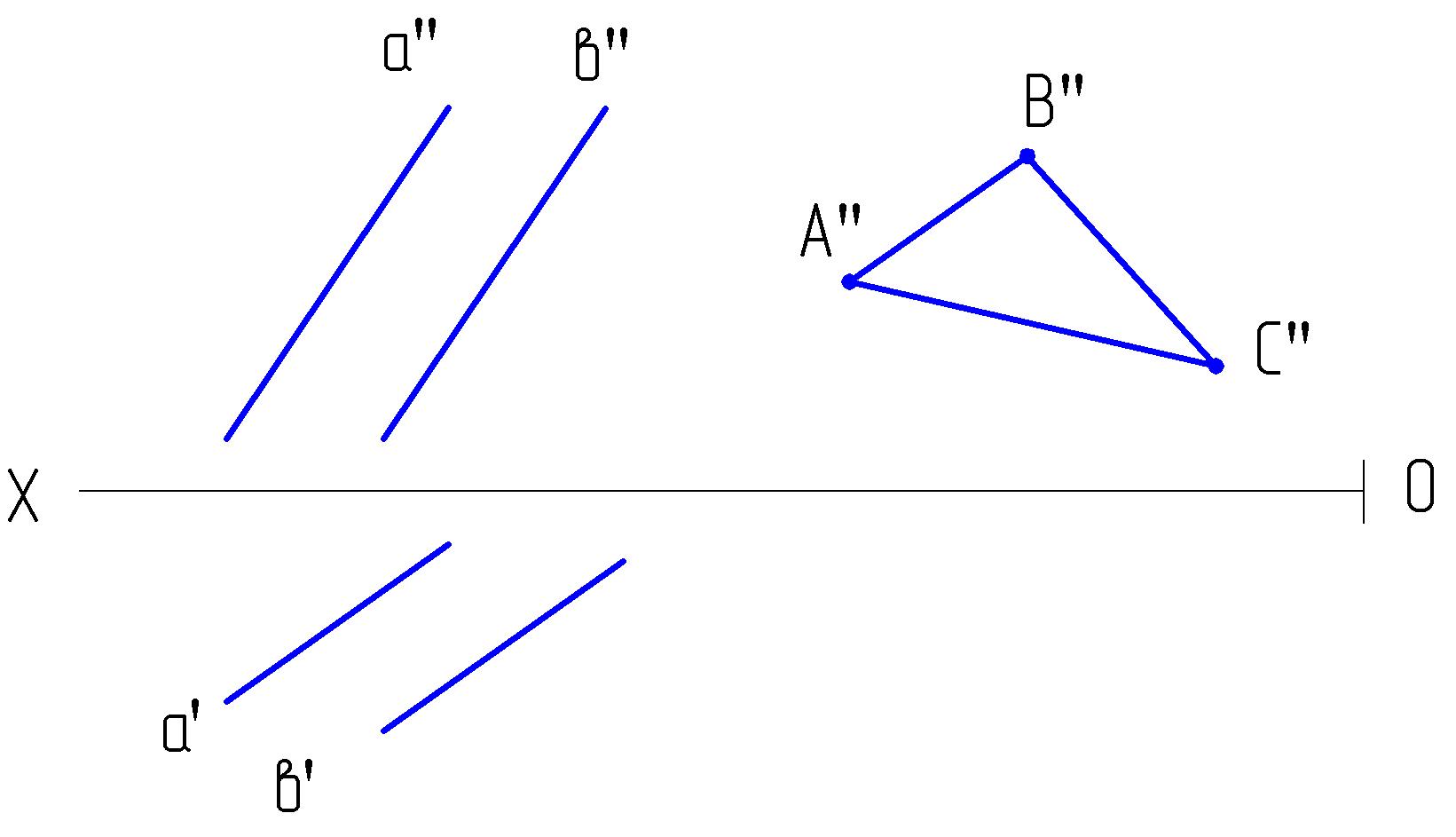
б) следами.
ТЕМА 3. поверхности. ТОЧКа и линия на поверхности.
3.1. Построить ряд образующих косой плоскости (а, в, α) и горизонтальную проекцию точки D, принадлежащей этой поверхности.
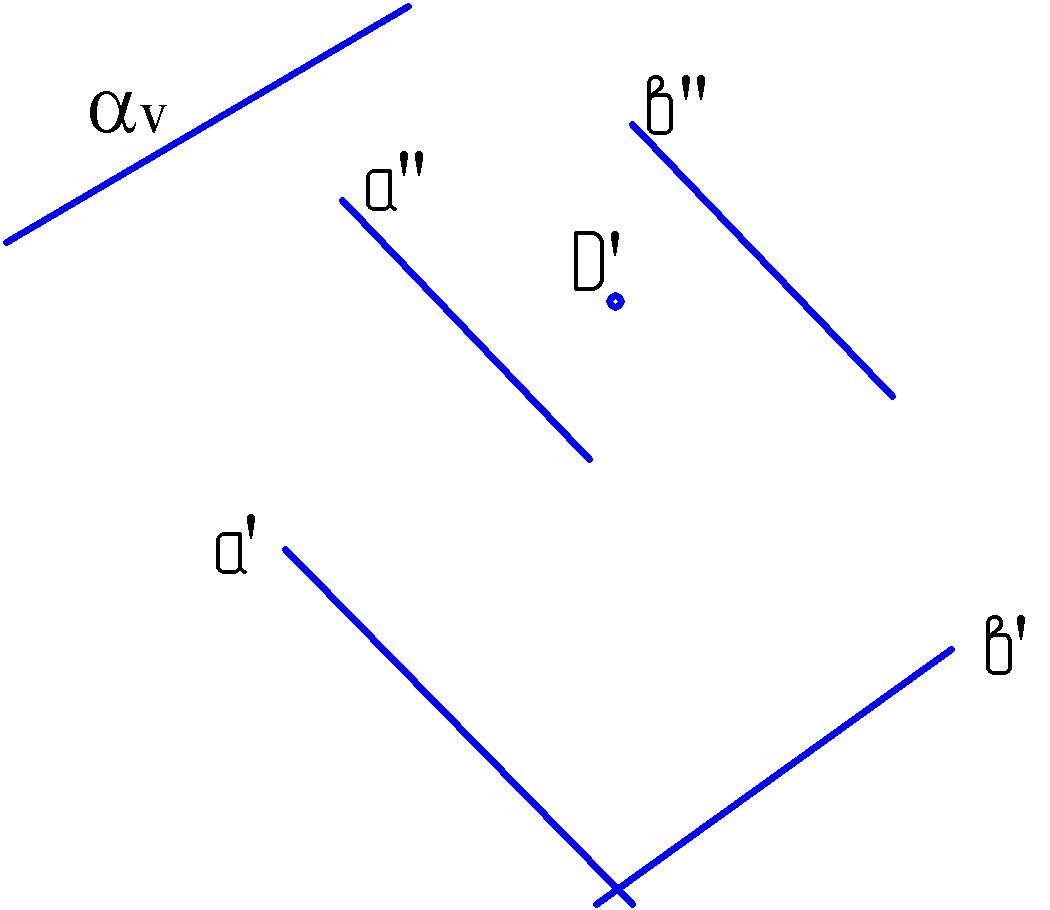
3.2. Построить очерк однополостного гиперболоида α (n; l).
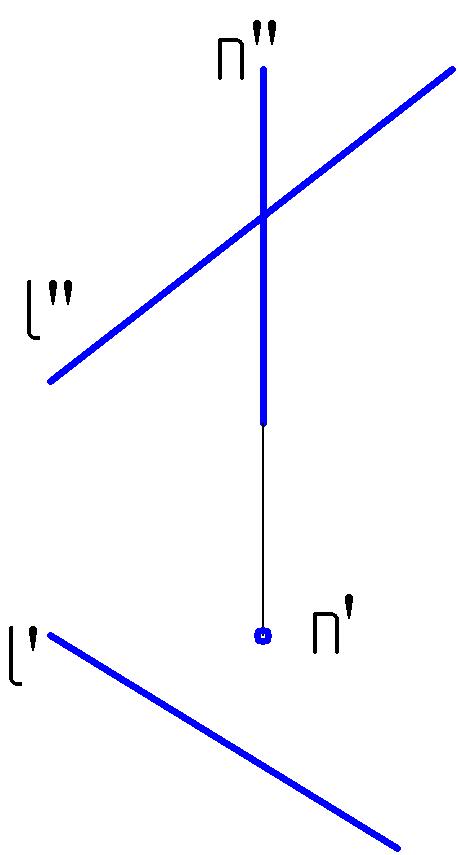
3.3. Построить недостающие проекции точек А и В, принадлежащих тору γ (К, l) и его очерк.
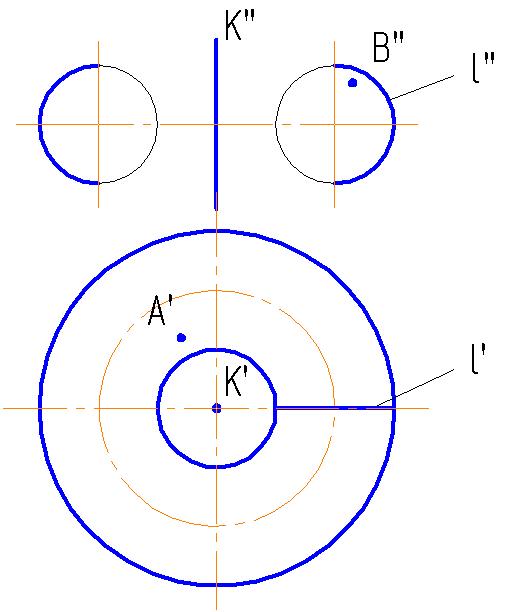
3.4. Построить образующие косого геликоида λ (а, к, γ°) и фронтальную проекцию точки В, принадлежащей геликоиду λ.
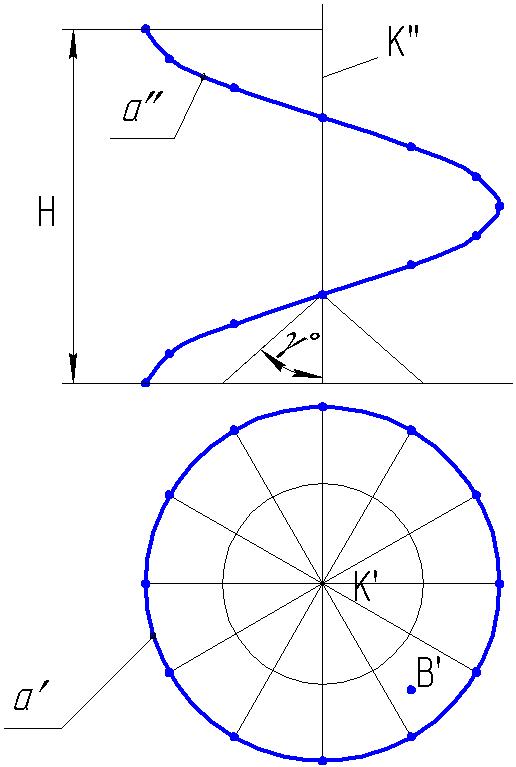
3.5. Построить недостающие проекции точки С и отрезка АВ, принадлежащих поверхностям вращения.

3.6. Построить недостающие проекции точки К и отрезка MN, принадлежа щих многогранникам.
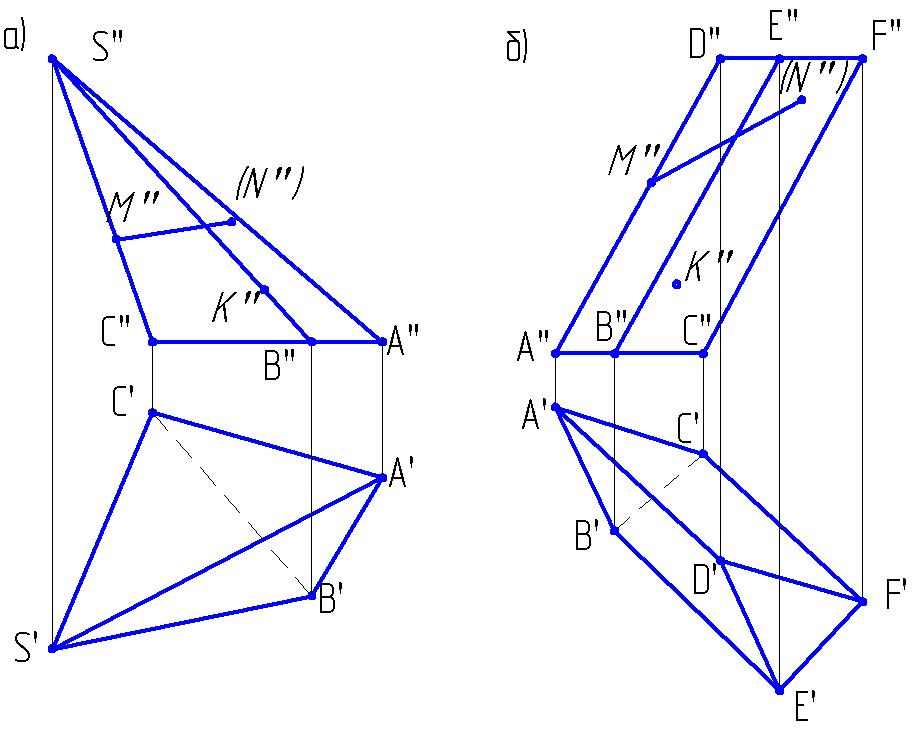
ТЕМА 4. Позиционные задачи.
4.1. Построить линию пересечения двух плоскостей:
а) α (а∩в) и (v) б) α (αv, αн) и (v)
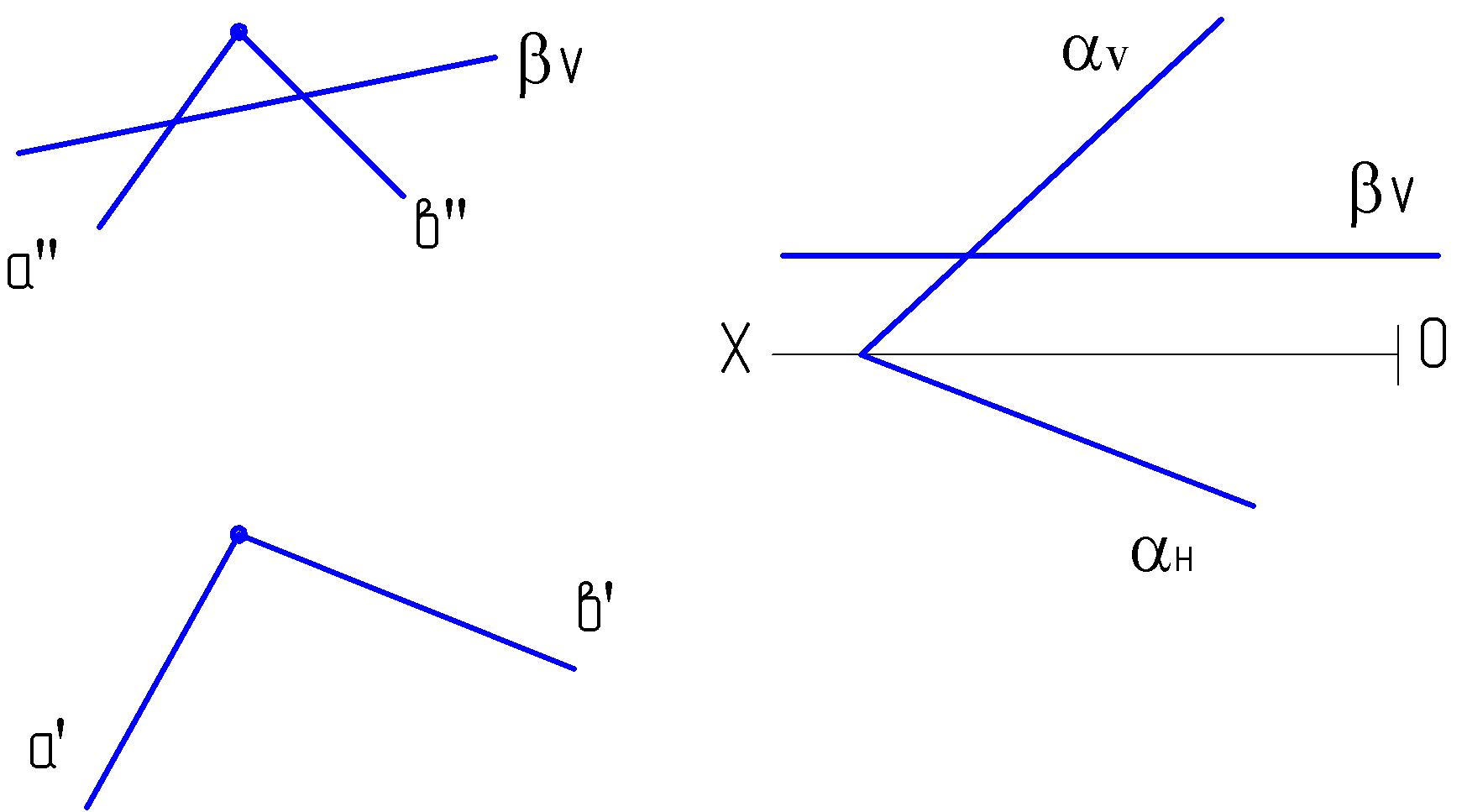
4.2. Построить линию пересечения двух плоскостей α (αv, αн) и (ΔАВС).
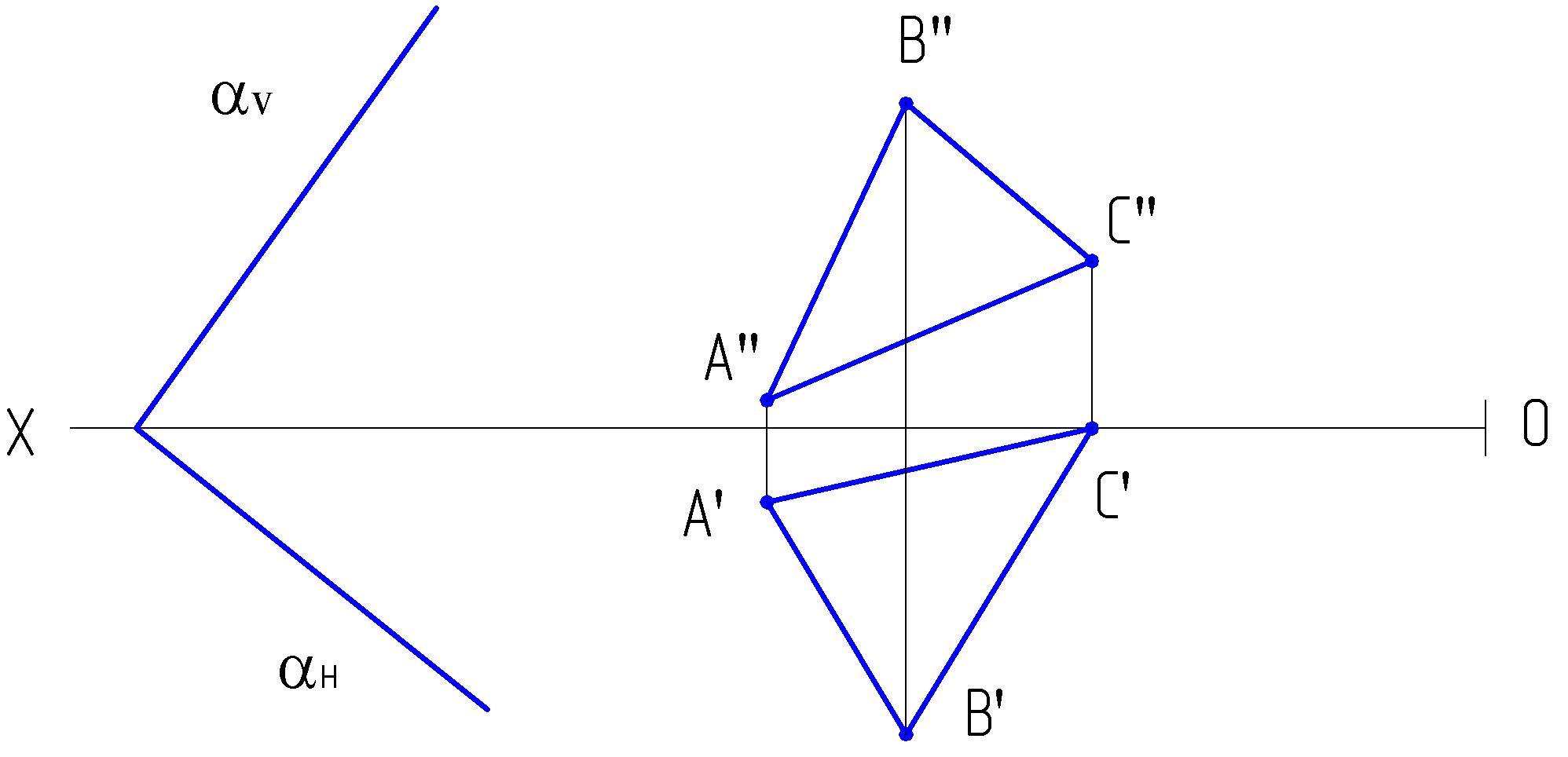
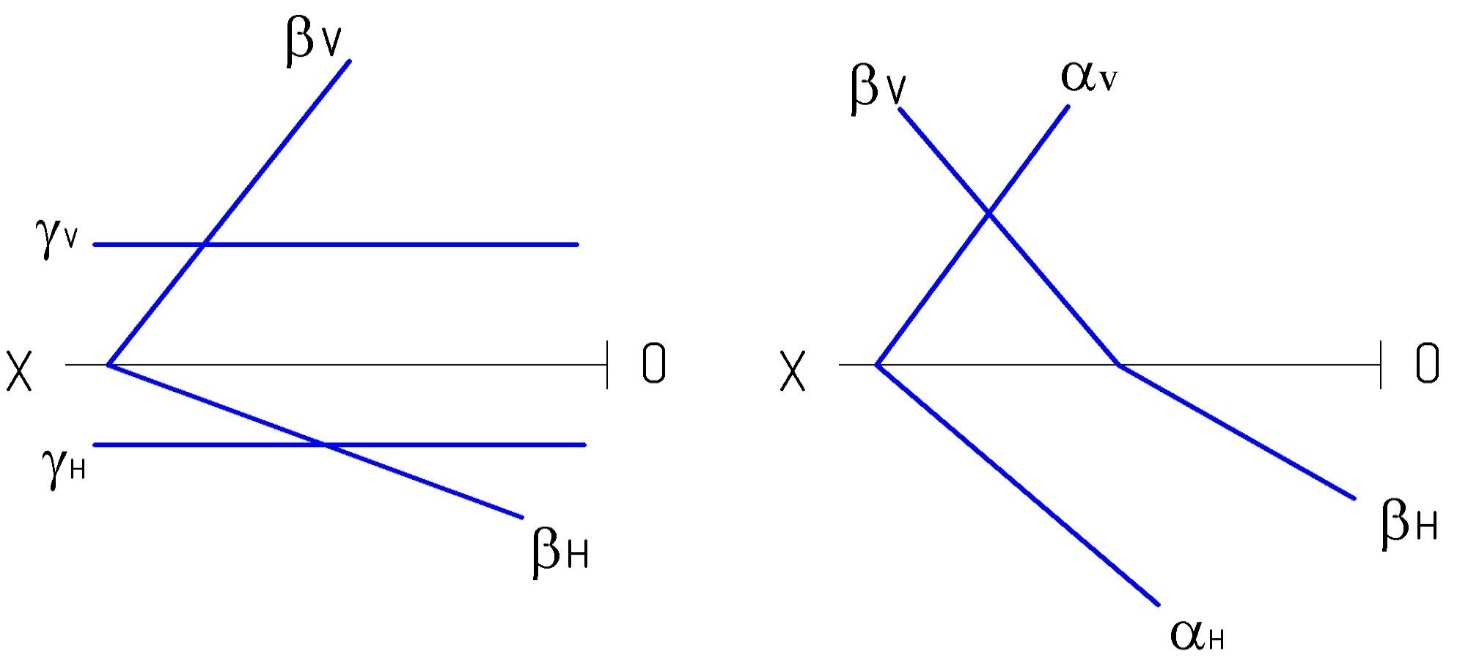
4.3. Построить линию пересечения двух плоскостей:
а) (v; н) и γ (γv; γн) б) α (αv, αн) и (v; н)
4.4. Построить линию пересечения цилиндра и сферы.
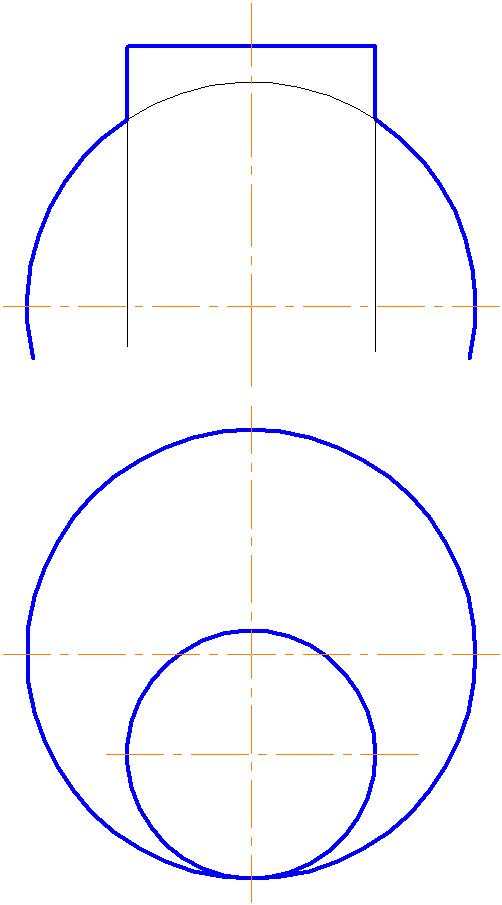
4.5. Построить линию пересечения поверхностей. Проанализировать изменение проекций линии пересечения поверхностей в зависимости от соотношений диаметров цилиндра и конуса. Определить видимость.
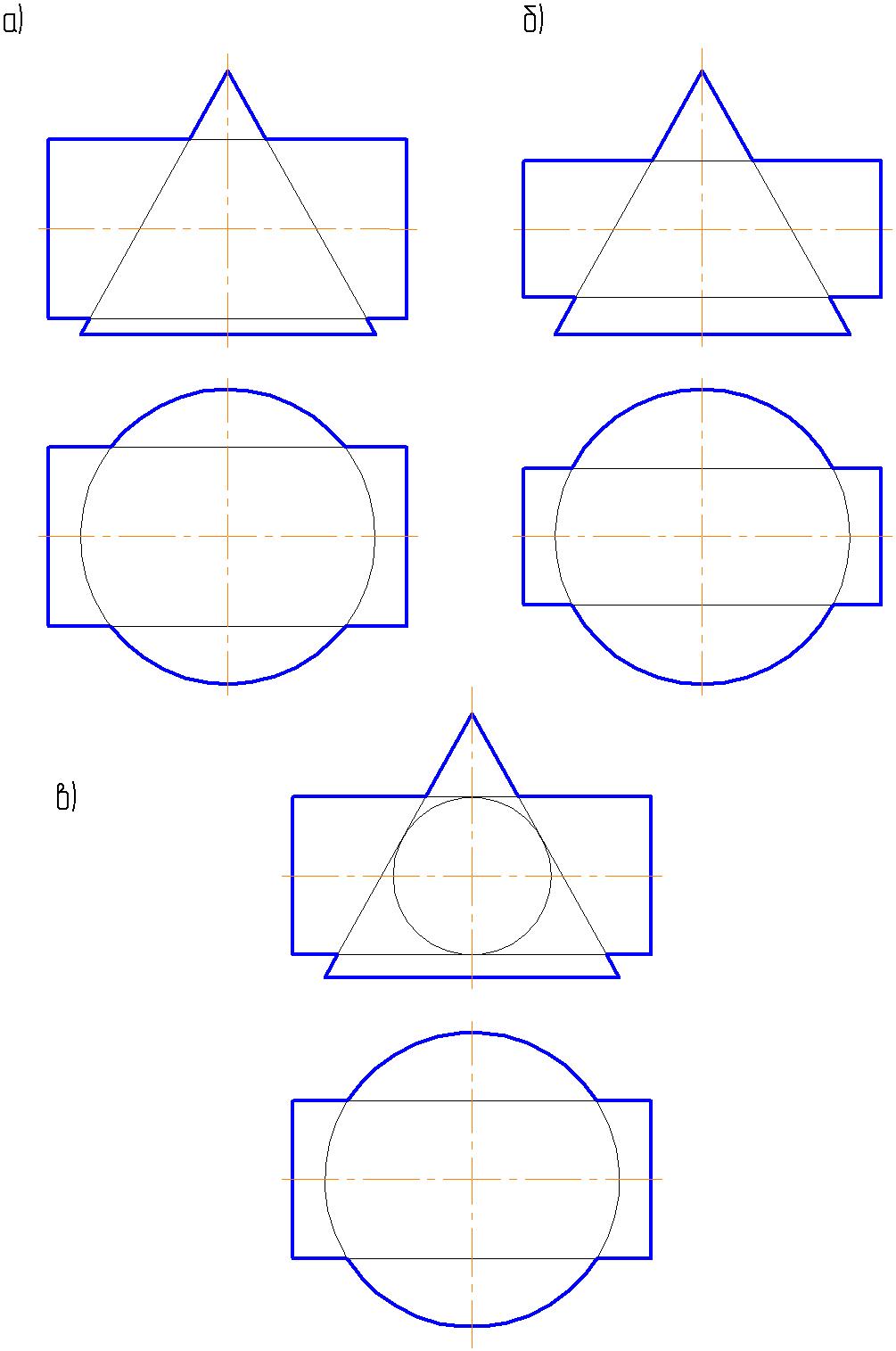
4.6. Построить точку пересечения прямой l с плоскостью α. Записать символами алгоритм решения.
а) α (αн: αv)
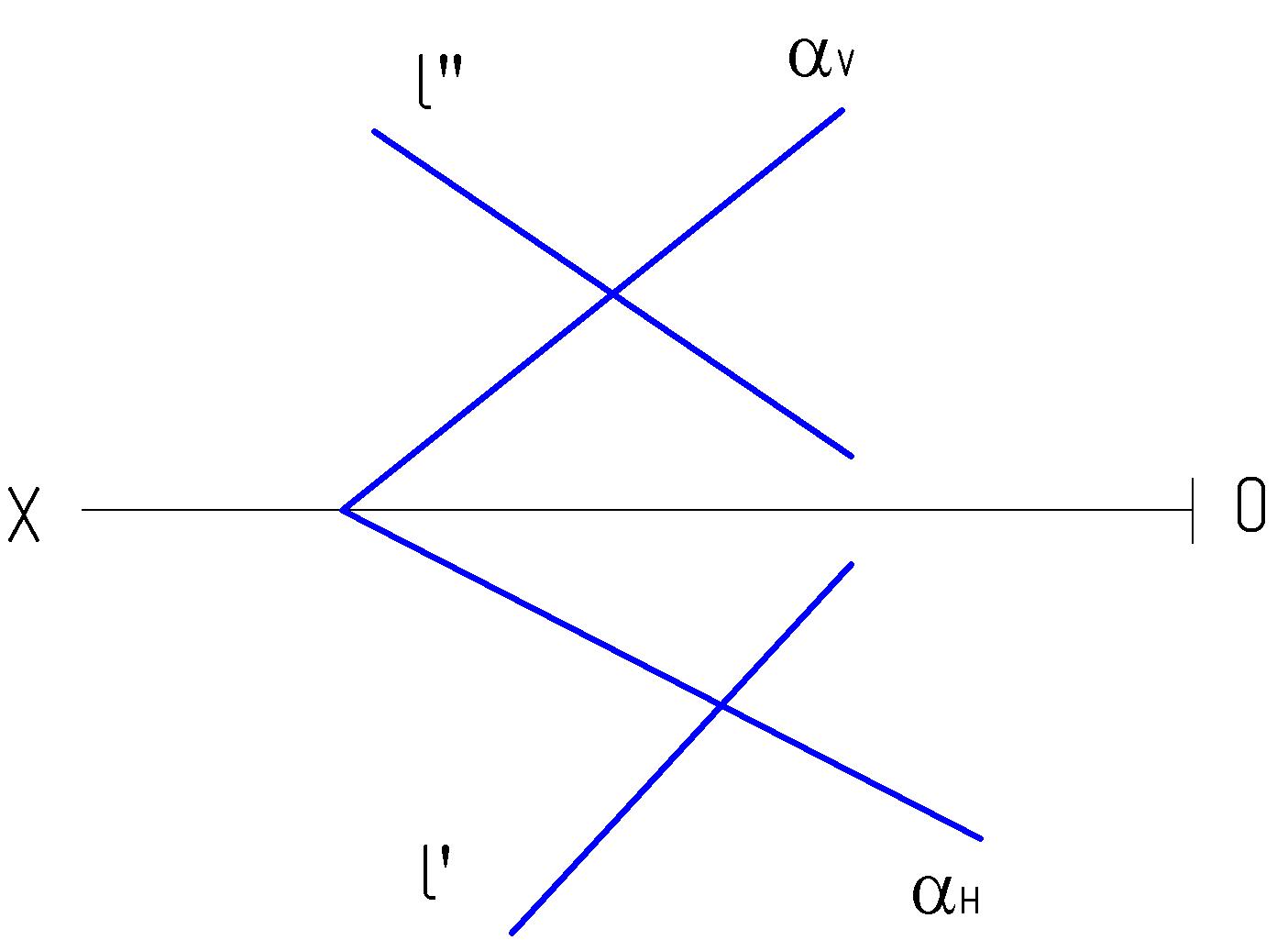
1.
2.
3.
111111111111111
б) α (а в)
1
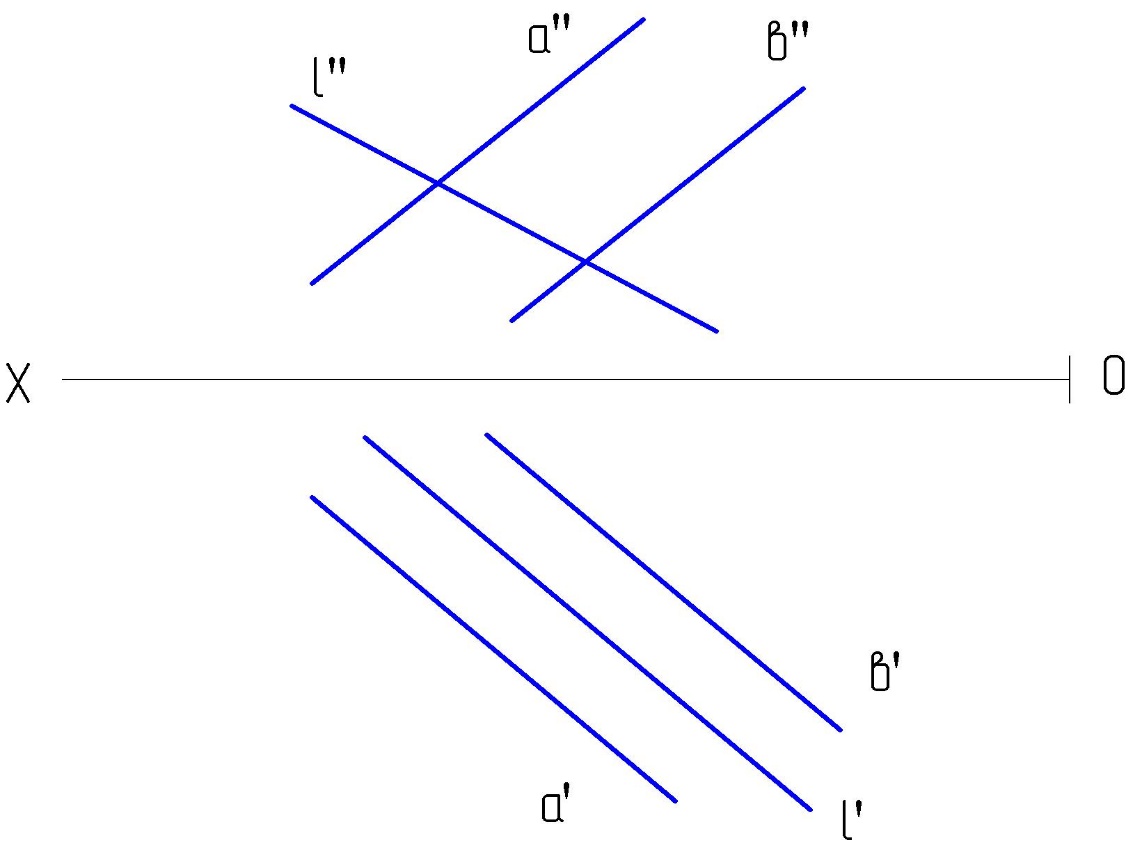 .
.2.
3.
4.7. Через точку А провести прямую, параллельную плоскости α (а∩в) и пересекающуюся с прямой l.
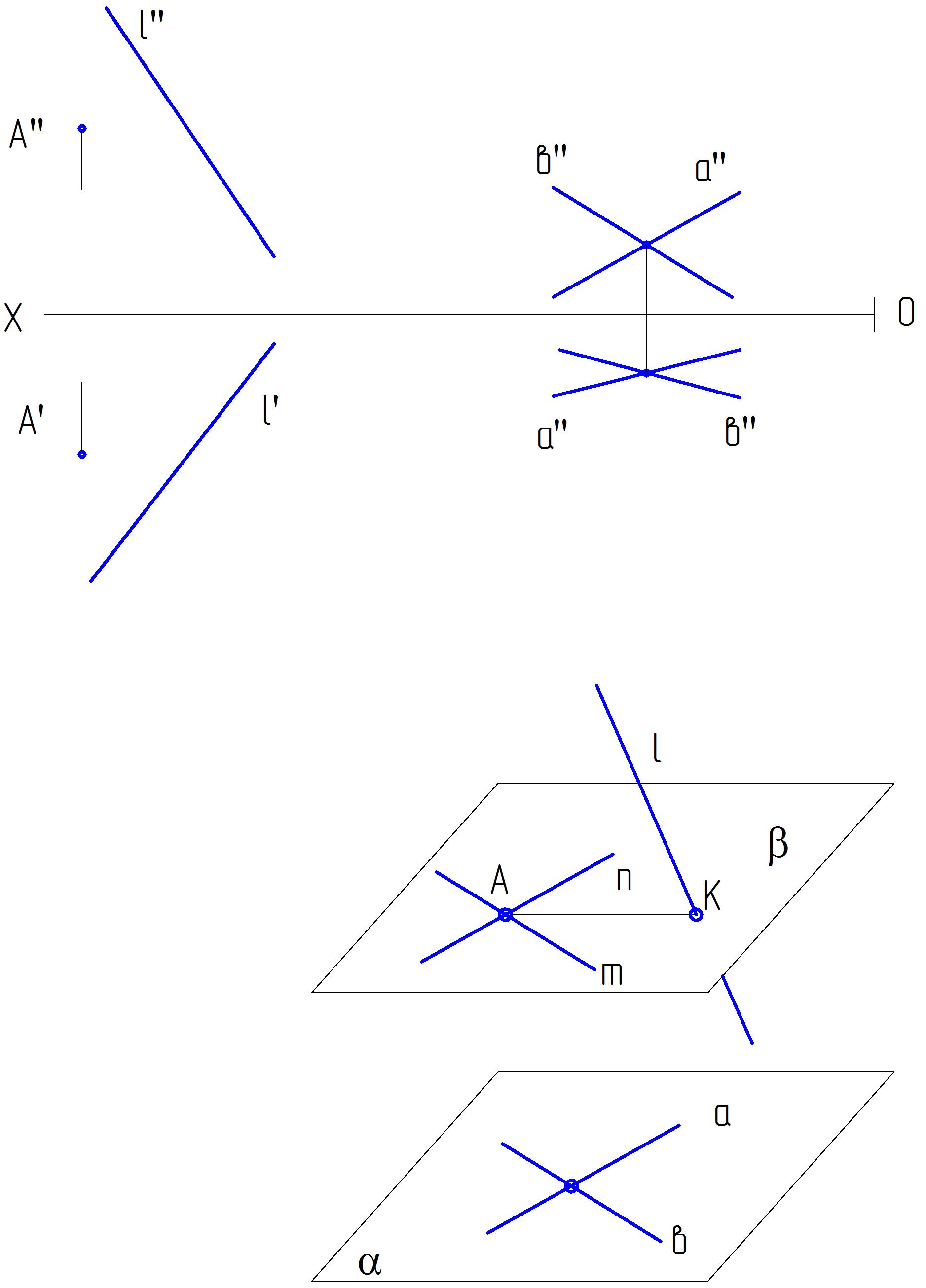


Решение (см. пространственный чертеж):
1. Через точку А проводим плоскость (n∩m),
параллельную данной
2. Найдём точку К пересечения
прямой l и плоскости : К=∩l
3. Соединяем точки А и К,
полученный отрезок
удовлетворяет всем
условиям задачи:
-
АК α -
АК ∩ l
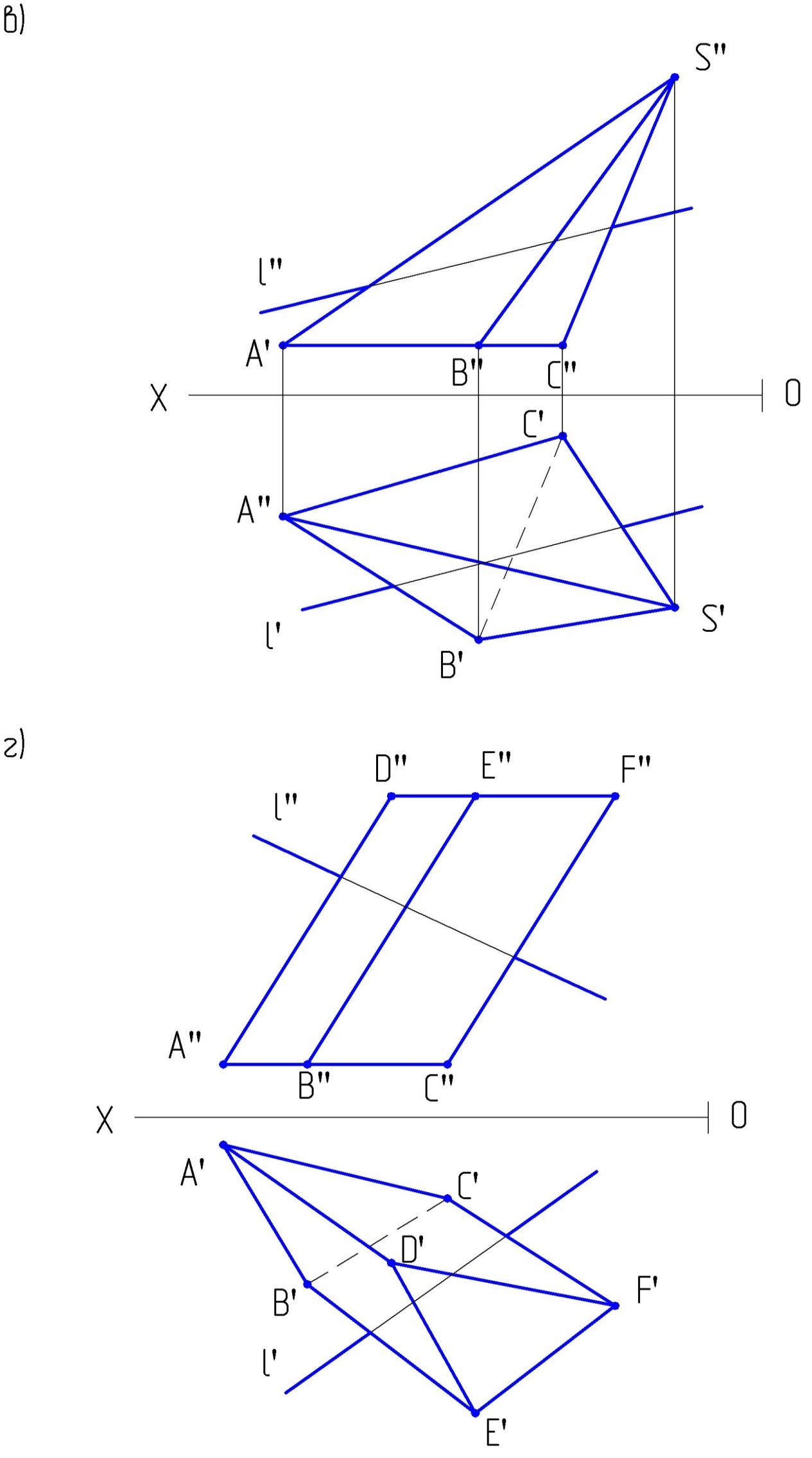
4.8. Определить точки пересечения прямой l с поверхностями. Определить видимость прямой l. Записать символами алгоритм решения.

1.
2.
3.
1.
2.
3.
Т
 ЕМА 5. Метрические задачи.
ЕМА 5. Метрические задачи.5.1. Определить расстояние от точки А до плоскости.