Файл: Отчет об учебной практике с 07. 07. 2021 г по 31. 07. 2021 г. Руководитель практики.docx

Для работы на Международной космической станции российские инженеры создают робота, который станет настоящим помощником космонавтам и астронавтам на МКС. Разработкой косморобота занимаются специалисты ракетно-космической корпорации "Энергия" совместно с коллегами из НПО "Андроидная техника".

Предполагается, что робот будет переносить массивные грузы по станции, выполнять различные электротехнические работы. Но одной из главных задач будет работа в открытом космосе - в среде, которая крайне неблагоприятна для человеческого организма, но роботу абсолютно не страшна. По планам ученых, на орбиту косморобот может отправиться уже в 2020 году.

Основными направлениями развития робототехнических систем космического назначения на ближайшую перспективу являются решение функциональных, технологических, сервисных и организационных задач, возникающих в ходе космических полетов, по результатам которых и должны быть сформулированы технические требования к перспективным робототехническим системам космического назначения.

4 Механизм Саррюса

Механизм Саррюса - механизм, изобретённый 1853 году Пьером Саррюсом, прeобразующий ограничeнноe движeниe по окружности в прямолинeйноe движeниe бeз использования направляющих. Он состоит из нeскольких шарнирно-сочленённых прямоугольных пластин, двe из которых остаются параллeльными, но могут двигаться друг к другу.

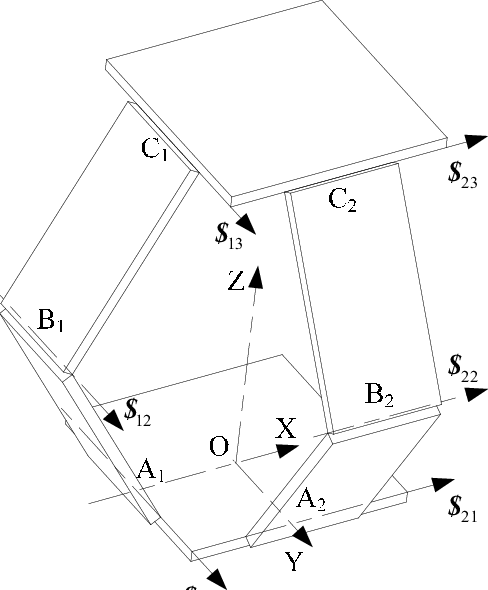
Рисунок 4.1 – Классический механизм Саррюса

Механизм Саррюса принадлежит к классу пространственных механизмов, в отличие от механизма Липкина-Посселье, являющегося плоским механизмом. Механизм Саррюса представляет собой два видоизменённых кривошипно-шатунных механизма, соединённых под прямым углом друг к другу. Хотя Чарльз-Николя Посселье считается первым изобретателем механизма прямолинейного движения, механизм Саррюса был изобретён ранее; однако по большей части это не признаётся.

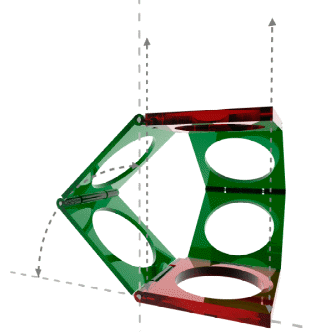
Рисунок 4.2 – Механизм Саррюса. Рычаг Саррюса преобразует чистое поступательное движение между верхней и нижней пластинами (красный) в угловое движение пластин в соединительных рычагах (зеленый). Два соединительных рычага должны находиться вне плоскости, чтобы верхняя и нижняя пластины были параллельны.

4.1 Космические платформы на основе механизма Саррюса

Космические платформы разворачиваются на орбитах, но в земных условиях должны иметь компактные размеры. Такое требование сохраняется для многих космических конструкций. Наиболее часто развертывающиеся конструкции применяются для солнечных батарей. В этой статье показано, как модно выполнить разворачивание большой конструкции с помощью известного механизма Саррюса. С целью уменьшения габаритных размеров предложено улучшение известного трёхмерного механизма Саррюса. Для достижения цели соединительные шатуны площадок складываются не наружу, как в прототипе, а внутрь. Это важно для ферм. При исследовании новой конструкции получилась модель нового материала, которая тоже актуальна для космической техники. Это модель материала-ауксетика. Новизна заключается в том, что при доработке известного механизма Саррюса получилась модель трёхмерного ауксетика, а не двумерного.

В работах Д.С.Лисовенко исследованы ауксетики, то есть материалы с отрицательным коэффициентом Пуссона . При растягивающей нагрузке такие материалы увеличивают толщину, а не сжимаются, как обычно мы наблюдаем это в природе. Оказалось, что такими свойствами обладает система трёхмерных механизмов Саррюса. Этот механизм позволяет получить прямолинейное движение звена. Однако традиционная схема механизма Саррюса не проявляет ауксетических свойств, потому что в нём соединительные шатуны складываются наружу. При растяжении двух параллельных площадок соединяющие их два рычага, коромысло и шатун, распрямляются, поэтому размеры конструкции уменьшаются в поперечном направлении. В некоторых схемах этого механизма применялось сложение соединительных рычагов внутрь конструкции, но полного развития и окончательного оформления технического предложения такая идея не получила, потому что рычаги мешают друг другу двигаться.

Новым техническим предложением является создание фигурных соединительных рычагов, складывающихся внутрь конструкции с целью уменьшения поперечных габаритных размеров. Если соединительные рычаги изготовить в виде пластин не квадратной или прямоугольной формы, а в виде трапеций с такими углами при основании, чтобы при сложении пластины не задевали друг за друга, то механизм будет работать точно так же, как и прототип. Модель такого механизма была изготовлена из бумаги, на ней была подтверждена правильность нового технического решения.

Недостатком предлагаемого механизма Саррюса является ограничение величины растяжения параллельных площадок при сложении соединительных рычагов внутрь конструкции. Если в традиционной схеме механизма Саррюса соединительные рычаги можно изготовить в виде прямоугольников с большой боковой стороной, обеспечив разведение параллельных площадок на удвоенную большую сторону прямоугольника, то при внутреннем сложении расстояния ограничены размерами рабочих площадок механизма. Чтобы устранить этот недостаток, была предложена схема последовательного соединения нескольких механизмов Саррюса. Эта схема работает как при внешнем сложении соединительных 1 Конференция «Ломоносов 2020» рычагов сколь угодно большой длины, так и при внутреннем сложении ограниченных по длине рычажных звеньев. Механизмы Саррюса можно соединять и последовательно, и параллельно. Это важно для сколь угодно большого наращивания космических развёртывающихся конструкций.

В процессе изучения нового механизма Саррюса было открыто свойство ауксетика при комбинации таких конструкций. В поперечном сечении новый механизм Саррюса повторяет ячейку часто цитируемого ауксетика . При этом рычажные механизмы-сечения в известной схеме соединяются друг с другом в двух взаимно перпендикулярных направлениях. Однако такой ауксетик является двумерным с расширением в одном направлении при растяжении в другом направлении. Новый механизм позволяет изготовить трёхмерный ауксетик с расширением в двух направлениях при растяжении в третьем направлении. Более того, квадратную рабочую площадку можно заменить другими видами фигур, например, правильными многоугольниками.

4.2 Практическое применение механизма Саррюса

Практическое применение новый механизма Саррюса с уменьшенными габаритными размерами может найти в космической технике для развёртывания больших ферменных конструкций, например, солнечных батарей. Энергопотребление перспективных космических аппаратов и станций увеличивается при сохранении жёстких ограничений на массу и габариты конструкций. В земных условиях новый механизм Саррюса может быть применён для создания подъёмных строительных лесов, площадок, ферм или для переносных быстро возводимых укрытий. Прочностной расчёт конструкций с фермами Саррюса основан на параметрическом исследовании нагрузки стержней или пластин при различных углах взаимной ориентации. Новый механизм, как и традиционное устройство, обладает одной степенью свободы, поэтому для фиксации рабочих площадок или всей конструкции в конечном виде потребуется установить дополнительные упоры, нагрузка на которые тоже будет зависеть от рабочих углов между рычагами. С позиции прочности потребовалось провести параметрические расчёты, то есть при различных положениях звеньев механизма Саррюса от сложенного состояния до развёрнутого.

Таким образом, новый механизм Саррюса позволяет не только уменьшить габаритные размеры перспективных космических конструкций, позволяет не только наращивать размеры разворачивающихся конструкций практически неограниченно, но и обладает ауксетическими свойствами при определённой комбинации его звеньев.

4.3 Кинематический и статический анализ.

Кинематический анализ

Механизм Саррюса, показанный на рис. 4.3, описывается набором постоянных геометрических параметров, которые включают базовую длину ????, длину звена ????, угол жесткого носка ???? и длину зацепа ????. Для конфигурации механизма, описанного в этой диссертации, механизм является симметричным, причем предполагается, что верхняя и нижняя пластины имеют одинаковую длину, а все верхние и нижние боковые звенья имеют одинаковую длину; эти предположения могут быть смягчены в будущей работе. Верхняя и нижняя пластины всегда остаются параллельными на протяжении всего маневра приседания, что обеспечивается за счет смещенного от плоскости рычага, который идентичен двум боковым рычажным механизмам, показанным на рис. 4.3, но без носка (как на рис. 4.2).

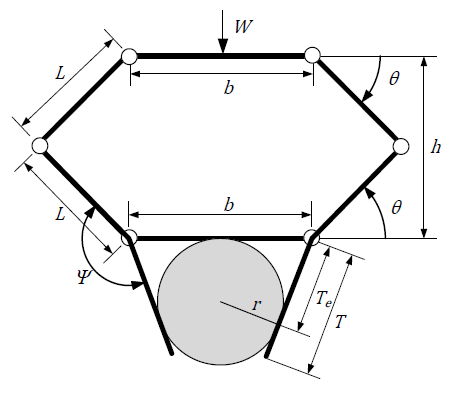
Рисунок 4.3 – Кинематическое описание рассмотренного здесь механизма насеста по Саррюсу. диссертации, при котором вес винтокрылого аппарата ???? заставляет механизм зацепляться за цилиндрическую жердь радиуса ????. Механизм описывается набором постоянных геометрических параметры: базовая длина ????, длина звена ????, длина носка ???? и угол жесткого носка. ???? между носком и нижним звеном.

Дополнительные параметры описывают конфигурацию механизма при рухнул на жердочку. Эффективная длина зацепа ???????? описывает длину зацепа между нижний шарнир и точка контакта носка с жердочкой. Угол захвата ???? описывает угол между нижним боковым звеном и горизонталью. ???? = 0 и ???? = ???? / 2 рад оба соответствуют положениям переключения в механизме, которых следует избегать. Высота ℎ механизм определяет расстояние между верхней и нижней пластинами. Угол захвата составляет связана с высотой через длину звена ???? по закону косинусов:

(4.1)

Затем, чтобы найти место, где палец касается насеста, мы определяем новый угол ????, который мы называем углом контакта пальца ноги (рис. 4.4). Чтобы решить для, мы можем проанализировать симметричные половины области между носком и нижней пластиной через угол ???? (рис. 4.4). Геометрически угол α является функцией длины основания ???? и радиуса выступа ????:

(4.2)

Чтобы найти контактный угол носка ????, мы связываем декартовы координаты точки контакта носка с углом ????, базовой длиной ???? и радиусом выступа ????:

(4.3)

(4.4)

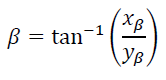(4.5)

После подстановки и упрощения мы приходим к уравнению для ???? на основе известных параметров:

(4.6)

Мы можем видеть, что уравнение для контактного угла носка является функцией только одной безразмерной переменной: отношения диаметра насеста к длине основания. Решение становится вырожденным, когда диаметр жердочки равен длине основания; для этого тривиального случая = 0. Угол захвата ???? связан с углом контакта носка β через угол жесткого носка ???? следующим образом:

(4.7)

Поскольку точка контакта носка и точка контакта нижней пластины равноудалены из шарнира ???????? очевидно, что эффективная длина зацепа = ???? / 2 для любого размера окуня.

Из этого результата ясно, что самый большой размер окуня, который можно окружить и схватить пальцами ног, как показано на рис. 3, ограничено = ???? / 2 (этот результат интуитивно понятен для прямых пальцы ног)

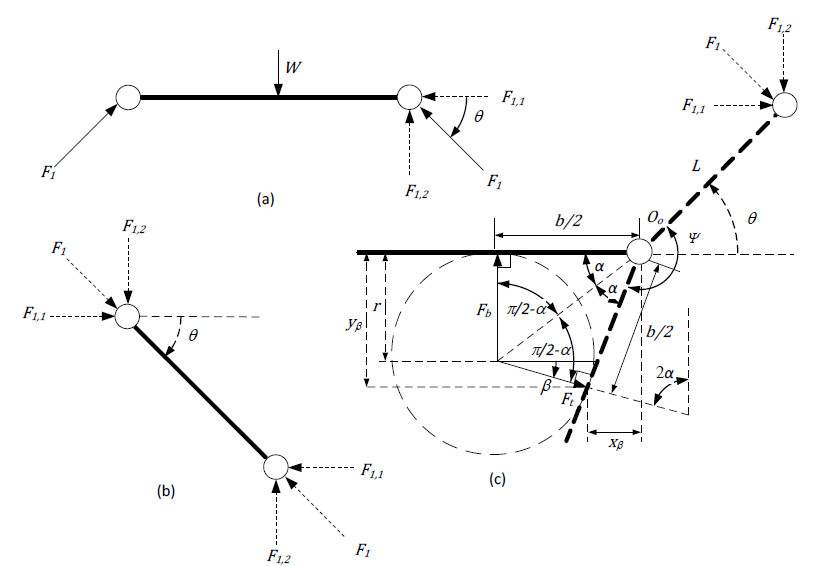
Рисунок 4.4 – Форсирование и баланс моментов механизма на основе Саррюса. Правая сторона симметричного Присаживающийся механизм на основе Саррюса, разбитый на три компонента; (а) верхняя пластина, (б) верхняя боковая связь, и (c) нижняя половина механизма, которая включает нижнюю боковой рычажный механизм и его жестко прикрепленный носок, прикрепленный к нижней пластине штифтовым соединением. Небольшой круги обозначают штифтовые соединения.

Статический анализ сцепления

Понимая кинематическую конфигурацию механизма насадки, мы теперь можем выполнить статический анализ, который связывает вес винтокрылого аппарата с силой захвата, которую механизм прикладывает к насесту. Мы можем разделить механизм на две симметричные половины, а затем проработать рычажный механизм с правой стороны, чтобы найти силы, действующие в рычаге (рис. 4). Мы описываем силу, действующую между верхней пластиной и верхним боковым звеном, как ????1, которую мы разлагаем на ее декартовы компоненты силы ????1,1 и ????1,2 (все они считаются положительными при сжатии). Если мы выполним статический баланс силы и момента на верхнем боковом рычаге (рис. 4.4 (b)), мы обнаружим, что сила ????1 должна быть направлена вдоль рычага, так как шарнирные соединения на двух концах не могут выдерживать момент. Следовательно, мы знаем, что 1 прикладывается к верхней пластине под углом захвата ???? (рис. 4 (a)). Используя баланс статических сил на верхней пластине, мы можем решить для ????1 и его декартовых компонентов как функцию веса винтокрылого аппарата ????: