ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.10.2024
Просмотров: 38
Скачиваний: 0
СОДЕРЖАНИЕ
Правила проведения суммативного оценивания
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 1 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 2 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 2 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 3 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 3 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 3 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 4 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 4 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 2 четверть
Продолжительность – 40 минут
Количество баллов – 20
Типы заданий:
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 5 заданий, включающих вопросы с кратким и развернутым ответами.
В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.
Характеристика заданий суммативного оценивания за 2 четверть
| Раздел | Проверяемая цель | Уровень мыслительных навыков | Кол. заданий * | № задания * | Тип зада ния* | Время на выполне ние, мин* | Балл* | Балл за разде л |
| Последова тельности | 9.2.3.2 Находить n-й член последовательности, например: 1 ; 1 ; 1 ; 1 ;... 2 3 3 4 4 5 5 6 | Применение | 1 | 1 | КО | 2 | 1 | 20 |
| 9.2.3.5 Знать и применять формулы n-го члена, суммы n первых членов и характеристическое свойство арифметической прогрессии | Применение | 1 | 2 | РО | 10 | 6 | ||
| 9.2.3.6 Знать и применять формулы n-го члена, суммы n первых членов и характеристическое свойство геометрической прогрессии | Применение | 1 | 3 | РО | 8 | 4 | ||
| 9.2.3.9 Применять формулу суммы бесконечно убывающей геометрической прогрессии к решению задач | Навыки высокого порядка | 1 | 4 | РО | 10 | 4 | ||
| 9.2.3.7 Решать текстовые задачи, связанные с геометрической и арифметической прогрессиями | Навыки высокого порядка | 1 | 5 | РО | 10 | 5 | ||
| ИТОГО: | | | 5 | | | 40 | 20 | 20 |
| Примечание:*-разделы,вкоторыеможновноситьизменения | ||||||||
Образец заданий и схема выставления баллов Задания суммативного оценивания за 2 четверть
-
Составьте одну из возможных формул n-го члена последовательности по первым пяти ее
членам:
2, 3 ,
4
4 , 5 ,
9 16
6 ,... .
25
[1]
-
В арифметической прогрессии первый член а1 10 и разность d 12 .
-
Найдите пятый член прогрессии
а5 и сумму первых пяти членов прогрессии S5 .
[3]
-
Обозначим n-й член прогрессии через an. Найдите наименьшее натуральное число n
такое, что an>370.
[3]
-
Три числа, из которых третье равно 12, образуют геометрическую прогрессию. Если вместо 12 взять 9, то эти числа составят арифметическую прогрессию. Найдите эти числа.
[4]
-
Первый, второй и третий члены геометрической прогрессии соответственно равны
2k 6; 2 k; k 2 , где k- положительное число. а) Найдите значение k.
b) Найдите сумму бесконечно убывающей геометрической прогрессии.
[4]
-
При хранении бревен строевого леса их укладывают, как показано на рисунке. Сколько бревен находится в одной кладке, если в ее основании положено 12 бревен?
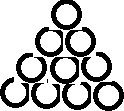
[5]
Схема выставления баллов
| № | Ответ | Балл | Дополнительная информация |
| 1 | а n1 n n2 | 1 | Принимается альтернативная запись |
| | а5 a1 4d 58 | 1 | |
| | S 2 10 4 12 5 5 2 | 1 | Или S 1058 5 5 2 |
| 2 | | | |
| S5 170 | 1 | | |
| | 10 (n1) 12 370 , 12n 372 | 1 | |
| | n 31 | 1 | |
| | n 32 | 1 | |
| 3 | b2 12bи b 9 b1 2 1 2 2 | 1 | Принимается альтернативное решение |
| b2 12(2b 9) , b2 24b108 0 2 2 2 2 D = 36 | 1 | ||
| b 18 и b 27 2 6 1 3 | 1 | | |
| 27, 18, 12 и 3, 6, 9 | 1 | | |
| | 4k2 (k 2)(2k 6) , k2 5k 6 0 | 1 | |
| | k1 1, k2 6 | ||
| | k 6 | 1 | |
| 4 | b 18 , q 2 1 3 | 1 | Принимается 18,12,8 и q 2 3 |
| | S b1 , S 18 54 1 q 1 2 3 | 1 | |
| 5 | a1 12 , d 1 | 1 | |
| an 1 | 1 | | |
| an a1 d(n1) , 1 12 (n1) | 1 | | |
| n 12 | 1 | | |
| S 12 1 12 78 n 2 | 1 | | |
| Итого: | 20 | | |

