Файл: Отчет представлен к рассмотрению Студент группы икбо21 мая 2023.docx

В листинге 3.1 представлено вычисление выражения, записанного в виде строки.

Листинг 3.1 – Преобразование и вычисление выражения

>>> import numexpr >>> expr = "x**2 + 2*x + 1" >>> x = 3 >>> print(numexpr.evaluate(expr)) 16 >>> for x in range(5): ... print(numexpr.re_evaluate(), end=' ') ... 1 4 9 16 25

3.2 Использование квазислучайных чисел

Рассчитанные с помощью псевдослучайных чисел значения определенных интегралов имеют существенные погрешности. Для повышения точности результатов можно попытаться увеличить количество итераций, но этот способ сильно ударит по производительности системы.

Так как случайные числа, генерируемые с помощью функции random.uniform(), не позволяют нам получить хорошую точность вычислений, заменим этот фрагмент программы на генерацию квазислучайных чисел.

Примером квазислучайной последовательности с низким расхождением является последовательность, введенная советским и российским математиком Ильей Мееровичем Соболем.

Последовательности Соболя реализованы во многих языках программирования. В Python мы будем использовать модуль scipy.stats.qmc, предоставляющий генератор Квази-Монте-Карло.

Генерация последовательности Соболя и сэмплирование чисел выглядит представлена в листинге 3.2.

Листинг 3.2 – Использование последовательности Соболя

>>> from scipy.stats import qmc >>> sequence = qmc.Sobol(2) # Генерация точек размерности 2 >>> sequence.random_base2(3) # Получение 2**3 точек последовательности array([[0.32530789, 0.4138235 ], [0.54991055, 0.5218935 ], [0.79678792, 0.00597485], [0.08001492, 0.92939895], [0.19777599, 0.23063183], [0.926283 , 0.84131181], [0.66449505, 0.32613319], [0.45943889, 0.74645907]])

4 Тестирование и анализ эффективности

В таблице 4.1 приведены результаты тестирование. Во всех случаях ошибка вычислений составляет не более 0,005%.

Таблица 4.1 – Результаты тестирования программы [разработано автором]

	Результат, полученный численным методом	Результат, полученный с помощью программы
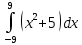	576	575.9999998750075
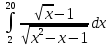	4.23130473194049	4.231304796742568
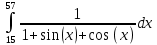	1.34344911060489	1.3434512748704621
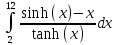	81303.7226750316	81304.12849936835

---

В таблице 4.2 представлена зависимость времени работы программы от количества используемых процессов.

Таблица 4.2 – Зависимость времени выполнения от количества процессов [разработано автором]

	Процессор
Запускаемые процессы		Intel Core i7 10700 8 cores / 16 threads	Intel Core i5 7600 4 cores / 4 threads	AMD Ryzen 5 3500U 4 cores / 8 threads	Intel Core i7 8565U 4 cores / 8 threads
	1	14.536 с	18.755 с	22.815 c	29.154 с
	2	7.561 с	9.543 с	12.469 с	14.119 с
	4	4.070 с	5.595 с	8.042 с	9.577 с
	8	2.390 с	6.328 с	6.967 с	8.916 с
	16	2.219 с	7.840 с	9.007 с	11.680 с
	32	3.852 с	11.357 с	12.598 с	16.837 с

Из представленной таблицы видно, что время вычисления интеграла с использованием всех доступных потоков процессора сокращается в несколько раз относительно времени вычисления с использованием одного потока.

Отметим, что при использовании процессоров, реализующих идею одновременной многопоточности (например, Hyper-Threading), операционная система определяет их каждое ядро как два логических процессора. Так как в этом случае у каждого логического процессора есть только собственные регистры и контроллер прерываний, а всё остальное физически является общим для них всех, мы не видим существенного ускорения программы.

ЗАКЛЮЧЕНИЕ

В ходе выполнения данной работы были изучены средства реализации параллельных вычислений в языке программирования Python. Были рассмотрены два основных способа организации параллельных процессов: на основе потоков и на основе процессов. Первый способ был реализован с помощью модуля threading, второй – с помощью модуля multiprocessing.

---

В ходе работы был разработан алгоритм нахождения определенного интеграла методом Монте-Карло с использованием параллельных вычислений в языке программирования Python. Тестирование показало увеличение вычислительной производительности процессора и тем самым доказало эффективность параллельных вычислений.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. 
   Python 3.10.4 documentation. The Python standard library. Concurrent Execution. Threading – Thread-Based parallelism – URL: https://docs.python.org/3/library/threading.html (дата обращения: 27.05.2023).
   
2. 
   Python 3.10.4 documentation. The Python standard library. Concurrent Execution. Multiprocessing – Process-based parallelism – URL: https://docs.python.org/3/library/multiprocessing.html (дата обращения: 27.05.2023).
   
3. 
   Zaccone G. Python Parallel Programming Cookbook – Second Edition. – Packt Publishing Ltd., 2019 – URL: https://www.packtpub.com/product/python-parallel-programming-cookbook-second-edition/9781789533736 (дата обращения: 27.05.2023).
   

ИСТОЧНИКОВ НЕ МЕНЕЕ 15

ДОЛЖНЫ БЫТЬ ССЫЛКИ В ТЕКСТЕ НА ИСТОЧНИКИ

ПРИЛОЖЕНИЕ А

Разработанный программный код

Листинг А.1 – Программный код

from math import ceil, floor, log2 from multiprocessing import Pool, cpu_count from time import time from numexpr import evaluate, re_evaluate from scipy.stats.qmc import Sobol def monte_carlo(f: str, a: int, b: int, iters_log2: int) -> float: """ Return sum of the values of function `f` from `a` to `b` over `2^iters` iterations. """ sequence = Sobol(1).random_base2(iters_log2) f_sum = 0 evaluate(f, local_dict={'x': a + (b - a) * 0.5}) for r in sequence: x = a + (b - a) * r[0] f_sum += re_evaluate() return f_sum if __name__ == "__main__": expr = input("Подынтегральная функция: ") integrate_from, integrate_to = map(int, input("Границы интегрирования (a, b): ").split()) processes = int(input("Количество запускаемых процессов (0 - авто): ")) or cpu_count() if processes > 32: print("Количество процессов уменьшено до 32") processes = 32 total_iterations = int((integrate_to - integrate_from) * 4096) per_process_log2 = floor(log2(total_iterations)) - ceil(log2(processes)) total_iterations = 2 ** per_process_log2 * processes

Продолжение листинга А.1

print(f"Вычисление запущено...") start = time() with Pool(processes) as pool: results = pool.starmap(monte_carlo, ((expr, integrate_from, integrate_to, per_process_log2) for i in range(processes))) end = time() result = (integrate_to - integrate_from) * (sum(results) / total_iterations) print(f"\nОпределённый интеграл = {result}") print(f"Процессов: {processes}. Общее время вычисления: {(end - start):.3f} с")

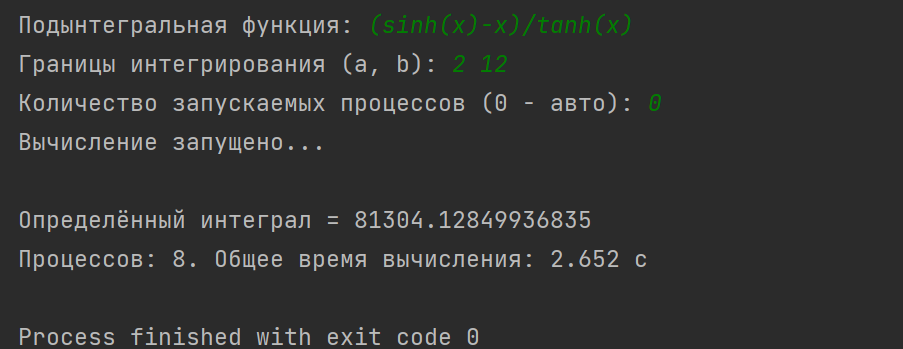На рисунке А.1 показано использование разработанного программного кода.

Рисунок А.1 – Использование программного кода

---

Разработанный программный код и файлы тестирования находятся в репозитории на GitHub: https://github.com/alex0d/parallel-computing

---