Файл: Отчет представлен к рассмотрению Студент группы икбо21 мая 2023.docx

Однако, разрабатывая программы с использованием параллельных вычислений, мы сталкиваемся с таким ограничением Python, как Global Interpreter Lock (GIL).

Уточним, что GIL – это ограничение CPython — наиболее распространённой, фактически эталонной реализации языка программирования Python, разработанной на языке программирования C. Например, Jython (реализация на языке Java) и IronPython (написан на C# и предназначен для платформы Microsoft .NET или Mono) не имеют GIL.

Концепция GIL заключается в том, что в каждый момент времени только один поток может исполняться процессором. Это сделано для того, чтобы между потоками не было борьбы за отдельные переменные. Исполняемый поток получает эксклюзивный доступ по всему окружению. Такая особенность реализации потоков в Python значительно упрощает работу с потоками и даёт нам потокобезопасность.

Из-за GIL производительность однопоточного и многопоточного процессов одинакова, т.к. глобальная блокировка делает любую программу однопоточной. Однако многие библиотеки успешно обходят это ограничение.

1. Параллелизм на основе потоков

Потоки содержатся внутри процессов и имеют общие данные и ресурсы. Иначе говоря, поток – это выделяемое процессорное время, а процесс – это заявка на все виды ресурсов (в т.ч. память).

Потоки не дают нам никаких преимуществ в производительности для тех задач, которые интенсивно используют вычислительную мощность процессор. Потоки чаще всего используются для задач ввода-вывода, связанных с внешними системами, т.к. они более эффективно работают вместе. Например, мы можем продолжить выполнение кода, пока ожидаем ввод от пользователя. Используя единственный поток выполнения, нам бы пришлось приостановить выполнение всей программы и ждать ввод.

Стоит также отметить, что контекстное переключение между процессами выполняется гораздо дольше, чем контекстное переключение между потоками, которые относятся к одному и тому же процессу. Это позволяет выигрывать в производительности при определенных сценариях.

В Python потоками управляет модуль threading, входящей в стандартную библиотеку. Данный модуль предоставляет нам все возможности для многопоточности программирования. Помимо объектов класса Thread, в нём есть множество объектов синхронизации, такие как Lock, Condition, Semaphore и другие.

В листинге 1.1 показана программа, выполняющая вывод в консоль из разных потоков.

---

Листинг 1.1 – Пример программы, использующей модуль threading

from threading import Thread def foo(iters): for i in range(iters): print(i) thread1 = Thread(target=foo, args=(10,)) thread2 = Thread(target=foo, args=(10,)) thread1.start() thread2.start() thread1.join() thread2.join()

Сначала создаются объекты потоков, где первый параметр – это «целевая» функция, второй – список позиционных аргументов, которые следует передать функции.

Метод start() запускает ранее созданный поток.

После запуска потока мы применяем join() – метод синхронизации, который блокирует вызывающий поток. Так только метод join() вернёт управление, главный поток сможет продолжить выполнение.

Вывод потоков не синхронизирован и будет выглядеть следующим образом: 0 1 2 0 1 2 3 3 4 5 4 6 5 6 7 8 7 8 9 9.

Сравним время, затраченное на печать 200000 чисел параллельно из двух потоков, с временем, затраченным на печать такого же количество чисел из одного главного потока. Для этого из модуля time импортируем функцию time, возвращающую время в Unix-формате.

Для получения времени работы программы будем окружать вызовами функции time только тот блок, который требует значительных вычислительных ресурсов и время выполнения которого не зависит от действий пользователя в момент выполнения (например, этот блок не должен содержать ввод исходных данных пользователем с клавиатуры).

Использование данной функции показано в листинге 1.2.

Листинг 1.2 – Пример использования функции time

from time import time # ---Code--- start = time() # Code to execute end = time() print("Time (s): ", end - start)

Полученный результат: 36.75 секунд при параллельном выполнении и 33.14 секунд при выполнении из главного потока. Видим, что программы выполнились примерно с одинаковой скоростью. Большее время в первом случае объясняется тем, что ОС приходится тратить некоторое процессорное время на переключение потоков.

2. Параллелизм на основе процессов

Процессы ускоряют операции на Python, которые создают интенсивную вычислительную нагрузку на процессор, используя сразу несколько ядер и избегая GIL.

Модуль Python multiprocessing, который является частью стандартной библиотеки самого языка, реализует параллельность на основе процессов. Он во многом схож с модулем threading, однако порождение процессов вместо потоков позволяет ему эффективно обходить GIL. Также multiprocessing реализует несколько интерфейсов, не имеющих аналогов в threading. Один из таких – объект multiprocessing.Pool, который мы будем использовать для распараллеливания нашей задачи. Число, которое будет передано в multiprocessing.Pool(), будет равно числу порожденных процессов. По умолчанию используется число, возвращаемое функцией multiprocessing.cpu_count() (количество потоков процессора). Далее объект автоматически распределит процессы по ядрам процессора.

---

Для работы с объектом multiprocessiong.Pool мы будет использовать оператор with, которые гарантирует, что все процессы будет уничтожены после завершения их работы.

Классический пример использования рассматриваемой библиотеки показан в листинге 1.3.

Листинг 1.3 – Пример программы, использующей модуль multiprocessing

from multiprocessing import Pool def foo(x: float) -> float: return x * x if __name__ == "__main__": with Pool() as pool: results = pool.map(foo, [1, 2, 3, 4]) print(results)

С помощью метода pool.map() мы передали исполняемую функцию и список элементов, к каждому из которых будет применена функция.

Для оценки эффективности параллелизма на основе процессов напишем код, который будет требовать значительных вычислительных ресурсов для выполения. К примеру, реализуем неоптимизированный метод определения простоты числа (Листинг 1.4).

Листинг 1.4 – Код для оценки эффективности использования multiprocessing

from multiprocessing import Pool from time import time def is_prime(k): if k > 1: for i in range(2, int(k / 2) + 1): if (k % i) == 0: return False else: return True else: return False

Продолжение листинга 1.4

if __name__ == "__main__": start = time() with Pool(4) as pool: res = pool.map(is_prime, range(100_000)) end = time() # # Вывод простых чисел # for i, num in enumerate(res): # if num: # print(i) print(end - start))

Зависимость времени исполнения от количества используемых процессов отражено в таблице 1.1.

Таблица 1.1 – Зависимость времени выполнения от количества процессов [разработано автором]

Количество процессов	Время выполнения
1	12.164 с
2	9.013 с
3	5.193 с
4	3.605 с

Наблюдается нелинейный прирост производительности. Запустив параллельно 4 процесса, нам удалось ускорить программу примерно в 3,5 раза.

Мы не сможем достичь пиковой производительности машины, принимаемой как произведение пиковой производительности одного процессора на число таких процессоров. Реальная производительности всегда будет ниже этого значения, так как данная величина зависит от архитектурных особенностей процессора, программной модели, эффективности компилятора, быстроты памяти и т.д.

---

На рисунках 1.1 и 1.2 показано использование потоков процессора при вычислениях с помощью одного и восьми процессов соответственно.




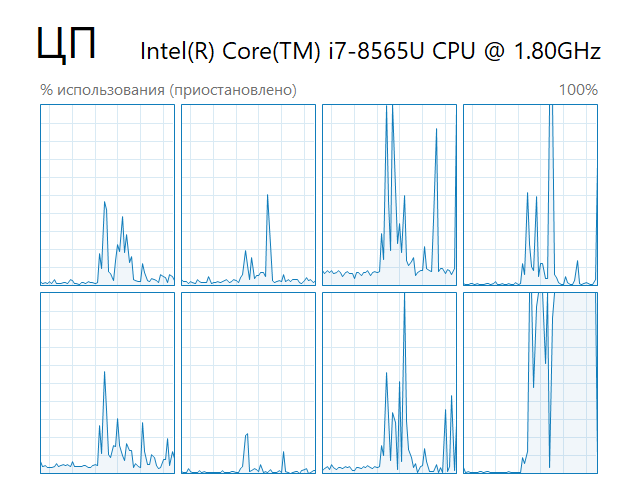
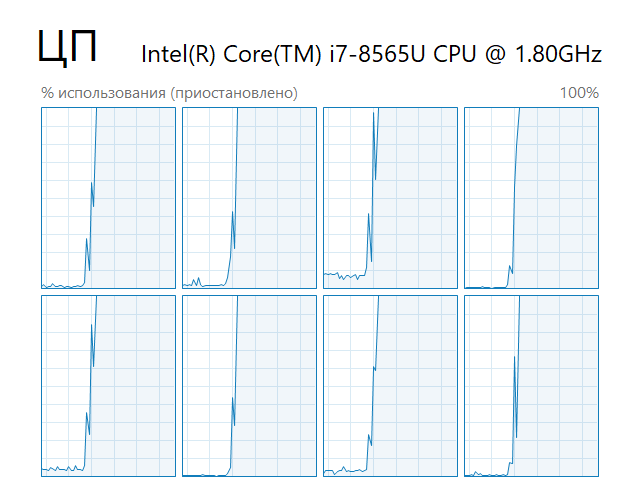
Рисунок 1.1 – Нагрузка на процессор при 1 запущенном процессе
[разработано автором]

Рисунок 1.2 – Нагрузка на процессор при 8 запущенных процессах
[разработано автором]


Мы видим, что во втором случае нагружены все потоки процессора. Однако следует помнить, что таким образом мы повышаем эффективность работы своей программы, фактически забирая все свободные ресурсы процессора в ущерб другим запущенным программам. Поэтому при разработке прикладных многопоточных приложений не рекомендуется использовать все имеющиеся потоки процессора.

2 Алгоритм нахождения определенного интеграла методом Монте-Карло

Методы Монте-Карло – это широкий класс вычислительных алгоритмов, в основе которых лежит моделирование случайных величин. Этот метод часто используется в физических и математических задачах и наиболее полезен, когда другие подходы использовать трудно или вовсе невозможно. Используется в различных областях математики, физики, химии, экономики, оптимизации и др.

Одно из наиболее частых применений метода Монте-Карло – вычисление определенного интеграла. Известно, что численные методы, такие как метод трапеций, эффективны, если интегрируемая функция гладкая. Также они теряют свою эффективность при увеличении размерности пространства.

В разрабатываемом программном коде мы реализуем следующий алгоритм вычисления :

1. 
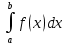   Сгенерируем N точек, равномерно распределенных на [a, b].
   
2. 
   Для каждой точки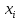 вычислим значение .
   
3. 
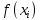   Вычислим выражение – формула (1):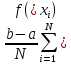
   

   (1)

4. 
   Получим оценку интеграла – формула (2):
   

---

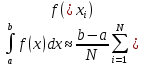(2)

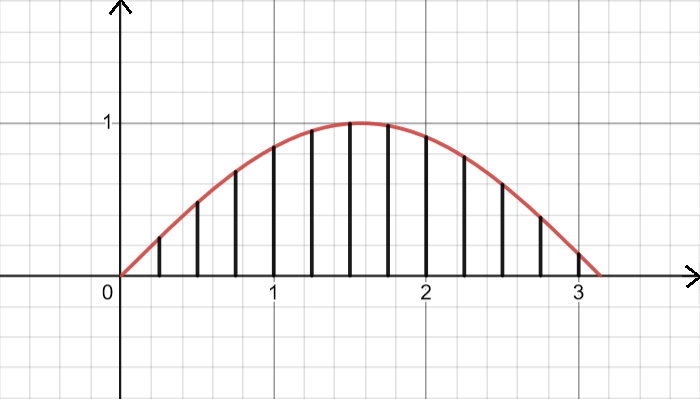
Рисунок 2.1 – Геометрическая интерпретация алгоритма
[разработано автором]
На рисунке 2.1 приведена графическая интерпретация данного алгоритма.

Этот способ во многом схож с определением определенного интеграла как площади криволинейной трапеции. Отличие состоит лишь в том, что вместо равномерного разделения области интегрирования на прямоугольники, мы «забрасываем» площадь интегрирования случайными точками. Далее мы можем сказать, что для равномерно распределенных точек ширина каждого получившего прямоугольника будет выражаться формулой .

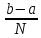3 Разработка программного кода

Разработанный программный код представлен в листинге А.1, пример его работы – на картинке А.1 (Приложение А).

Шаги, проделанные при создании кода, описаны ниже.

3.1 Ввод функции с клавиатуры

Разрабатываемая программа должна вычислять определенный интеграл функции, вводимой пользователем с клавиатуры. Для реализации такой возможности мы будем использовать модуль numexpr.

NumExpr — это библиотека Python для вычисления числовых выражений. Она обеспечивает лучшую производительность, чем NumPy, так как позволяет избежать выделения памяти для промежуточных результатов. Это приводит к лучшему использованию кэша и сокращает доступ к памяти в целом.

Библиотека поддерживает бинарные арифметические операторы +, -, *, /, **, % и множество математических функций. Приведем основные из них:

• 
  {sin,cos,tan}(float|complex): float|complex – тригонометрические синус, косинус, тангенс,
  
• 
  {arcsin,arccos,arctan}(float|complex): float|complex – тригонометрические арксинус, арккосинус, арктангенс,
  
• 
  {log,log10}(float|complex): float|complex – натуральный, десятичный логарифмы,
  
• 
  {exp}(float|complex): float|complex – экспонента,
  
• 
  sqrt(float|complex): float|complex – квадратный корень.
  

Модуль NumExpr довольно обширный и содержит также функционал для преобразования логических выражений.

Для вычисления выражений мы будем использовать две функции основные функции:

1. 
   evaluate(expression, local_dict=None, global_dict=None, optimization='aggressive', truediv='auto') – вычисляет выражение expression, по умолчанию подставляя в него значения из области вызываемой функции. Также аргументы могут быть указаны в local_dict или global_dict.
   
2. 
   re_evaluate(local_dict=None) – повторно вычисляет предыдущее выражение без каких-либо проверок. Функция предназначена для ускорения циклов, которые повторно вычисляют одно и то же выражение, не меняя ничего, кроме операндов.
   

---