Файл: О. В. Свеженцева Подпись И. О. Фамилия пояснительная записка.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 36
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
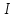 подставить комплекс тока
подставить комплекс тока 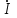 , вместо сопротивления
, вместо сопротивления  комплексное сопротивление
комплексное сопротивление 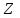 , вместо постоянной э.д.с.
, вместо постоянной э.д.с.  - комплексную э.д.с.
- комплексную э.д.с. 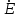 .
. Покажем применение комплексной арифметики к решению систем линейных алгебраических уравнений с комплексными коэффициентами методом обратной матрицы.
Пусть дана система

 линейных алгебраических уравнений с комплексными коэффициентами. Запишем ее в матричной форме:
линейных алгебраических уравнений с комплексными коэффициентами. Запишем ее в матричной форме: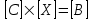 .
.В этой системе матрица коэффициентов
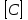 размерность
размерность  состоит из комплексных чисел
состоит из комплексных чисел 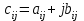 , где
, где 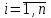 и
и 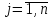 . Столбец неизвестных
. Столбец неизвестных 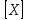 размерностью
размерностью  представляет собой также комплексные числа
представляет собой также комплексные числа 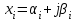 , где
, где 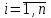 . Столбец свободных членов
. Столбец свободных членов 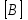 размерностью
размерностью  состоит также из комплексных чисел
состоит также из комплексных чисел 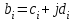 , где
, где 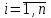 .
.Общепринятым приемом решения систем линейных алгебраических уравнений с комплексными коэффициентами является представление этой системы в виде двух систем линейных алгебраических уравнений
 - го порядка: отдельно для действительной части и отдельно для мнимой части. В итоге получаем вместо системы, состоящей из
- го порядка: отдельно для действительной части и отдельно для мнимой части. В итоге получаем вместо системы, состоящей из
 линейных алгебраических уравнений с комплексными коэффициентами, систему, состоящую из
линейных алгебраических уравнений с комплексными коэффициентами, систему, состоящую из 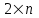 уравнений с действительными коэффициентами, в которой неизвестными являются действительные и мнимые части числа
уравнений с действительными коэффициентами, в которой неизвестными являются действительные и мнимые части числа 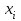 , т.е.
, т.е. 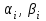 .
.Исходными данными в этой задаче будут выступать матрица коэффициентов
 и столбец свободных членов
и столбец свободных членов  . Для ввода матрицы коэффициентов зарезервируем двумерный массив с числом строк -
. Для ввода матрицы коэффициентов зарезервируем двумерный массив с числом строк -  , числом столбцов -
, числом столбцов -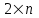 . Для ввода каждого из коэффициентов исходной системы отводится по две ячейки в строке: отдельно под действительную, отдельно под мнимую часть числа.
. Для ввода каждого из коэффициентов исходной системы отводится по две ячейки в строке: отдельно под действительную, отдельно под мнимую часть числа.Преобразуем исходную матрицу коэффициентов во вспомогательную матрицу коэффициентов размерностью
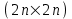 . Каждую строку исходной матрицы коэффициентов преобразуем в две строки во вспомогательной матрице. Покажем это преобразование на следующем примере: пусть исходная система линейных алгебраических уравнений с комплексными коэффициентами состоит из трех уравнений, запишем первое уравнение этой системы в общем виде:
. Каждую строку исходной матрицы коэффициентов преобразуем в две строки во вспомогательной матрице. Покажем это преобразование на следующем примере: пусть исходная система линейных алгебраических уравнений с комплексными коэффициентами состоит из трех уравнений, запишем первое уравнение этой системы в общем виде: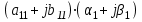
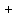
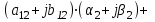
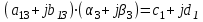
Раскроем скобки, перемножив попарно комплексные числа, и вновь представим эти произведения в виде комплексных чисел:
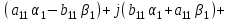
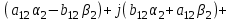
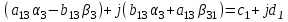
Приравниваем теперь правую и левую части последнего уравнения отдельно для действительной и отдельно для мнимой частей. В итоге имеем:

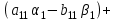
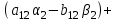
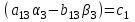
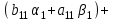
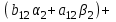
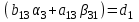
Таблица 1.1 - Комплексные коэффиценты
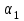 | 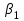 | 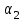 | 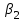 | 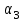 | 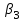 |
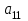 | 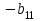 | 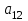 | 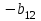 | 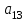 | 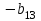 |
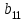 | 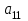 | 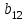 | 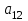 | 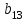 | 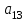 |
Последние две строчки в этой таблице дают фрагмент вспомогательной матрицы коэффициентов, соответствующий первому уравнению в нашей системе линейных алгебраических уравнений с комплексными коэффициентами. Аналогично строятся фрагменты во вспомогательной матрице коэффициентов, соответствующие второму и третьему уравнению в системе.
В итоге получаем вспомогательную матрицу коэффициентов размерностью
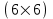 для нахождения
для нахождения 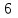 неизвестных
неизвестных  ,
,  ,
,  ,
,  ,
,  ,
,  . При условии, что детерминант этой системы не вырожден, находим решение этой системы методом обратной матрицы. Обозначим вспомогательную матрицу коэффициентов через
. При условии, что детерминант этой системы не вырожден, находим решение этой системы методом обратной матрицы. Обозначим вспомогательную матрицу коэффициентов через 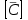 . Найдем обратную матрицу
. Найдем обратную матрицу 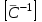 . Умножив эту матрицу на вектор-столбец свободных членов, найдем искомые неизвестные
. Умножив эту матрицу на вектор-столбец свободных членов, найдем искомые неизвестные  ,
,  ,
,  ,
,  ,
,  ,
,  .
. -
Исходные данные
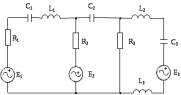
Рисунок 1.2 – Исходная схема
Таблица 1.2 – Исходные данные
| Вариант | 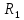 | 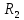 | 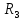 | 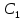 | 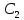 | 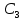 | 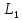 | 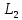 | 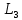 | 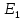 | 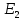 | 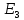 |
| 19 | 10 | 42 | 31 | - | - | 67 | 45 | - | 78 | 120 | 250 | 320 |
Выберем направления контурных токов
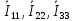 по часовой стрелке.
по часовой стрелке. Применяемые формулы для расчета:
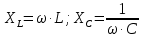 ;
; 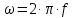
где:
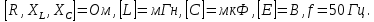
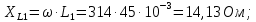
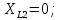
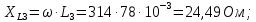
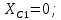
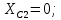
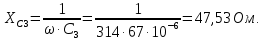
Запишем в общем виде уравнения для контурных токов:
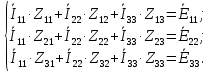
где:
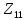 – собственное сопротивление первого контура, состоит из индуктивного и активного сопротивлений, соединенных последовательно:
– собственное сопротивление первого контура, состоит из индуктивного и активного сопротивлений, соединенных последовательно: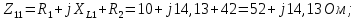
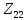 – собственное сопротивление второго контура:
– собственное сопротивление второго контура: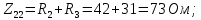
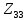 – собственное сопротивление третьего контура:
– собственное сопротивление третьего контура: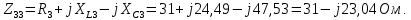

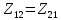 – сопротивление смежной ветви между первым и вторым контурами, взятое со знаком минус (знак минус взят, т.к. направления контурных токов в смежных ветвях противоположно):
– сопротивление смежной ветви между первым и вторым контурами, взятое со знаком минус (знак минус взят, т.к. направления контурных токов в смежных ветвях противоположно):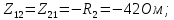
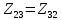 – сопротивление смежной ветви между вторым и третьим контурами, взятое со знаком минус (знак минус взят, т.к. направления контурных токов в смежных ветвях противоположно):
– сопротивление смежной ветви между вторым и третьим контурами, взятое со знаком минус (знак минус взят, т.к. направления контурных токов в смежных ветвях противоположно):