Файл: О. В. Свеженцева Подпись И. О. Фамилия пояснительная записка.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 37
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра электроснабжения и электротехники
Допускаю к защите
Руководитель ______ О.В.Свеженцева
Подпись И.О. Фамилия
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К курсовой работе по дисциплине
«Компьютерные, сетевые и информационные технологии»
1.019.00.00 ПЗ
Выполнил: студент группы ЭУмз-16-1 ___________ О.В. Орлова
Подпись И.О. Фамилия
Нормоконтроль ____________ О.В. Свеженцева
Подпись И.О. Фамилия
Курсовая работа защищена с оценкой _______________________
Иркутск, 2017
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
НА КУРСОВОЕ ПРОЕКТИРОВАНИЕ (КУРСОВУЮ РАБОТУ)
По курсу: Компьютерные, сетевые и информационные технологии
Студенту: гр. ЭУмз-16-1 Орлова О.В.
Тема курсового проекта (работы): Компьютерные, сетевые и информационные технологии, вариант № 19
Исходные данные: в соответствии с номером варианта
Рекомендуемая литература:
-
О.В. Свеженцева, Ю.В. Гаврилова. Вычислительная математика. Основные алгоритмы. МУ для выполнения лабораторных работ для студентов специальности 10.04. – Иркутск, 2002. - 23 с. -
Электротехника и электроника в экспериментах и упражнениях. Практикум на ElektronicsWorkbench в двух томах / Под ред. Д.И. Панфилова. –М.: “Додека”, ,2000 , т.2.-287 с. -
В.П.Дьяконов. Mathlab 6/5 SPI/7.0 +Simulink 5/6 в математике и моделировании. – М.: “СОЛН- Пресс”, 2005. -
В.Д.Сартаков. САПР в ЭП и информационные технологии в электроприводе. ч.2. Лабораторный практикум. – Иркутск, 2006. - 67 с.
Графическая часть на ____________листах
Дата выдачи задания «___» _________ 2016 г.
Задание получил __________ О.В. Орлова
Подпись И.О. Фамилия
Дата представления проекта (работы) руководителю «__»__________2017 г.
Руководитель курсового проекта (работы) ________ О.В.Свеженцева
Подпись И.О. Фамилия
СОДЕРЖАНИЕ
Введение 4
1.Символический или комплексный метод расчета разветвленных электрических цепей переменного синусоидального тока средствами Matlab 5
1.1.Теоретические сведения 5
1.2.Исходные данные 9
1.3.Решение задач линейной алгебры в системе MATLAB 10
2.Решение систем обыкновенных дифференциальных уравнений в среде MATLAB 11
2.1.Теоретические сведения 11
1.1.Исходные данные 12
1.2.Решение систем обыкновенных дифференциальных уравнений в системе MATLAB с помощью программного кода 13
3.Аппроксимация таблично заданной функции в средеMATLAB 15
3.1.Теоретические сведения 15
3.2.Исходные данные 17
Заключение 26
Список используемой литературы 28
Введение
Цель данного курса: связать математику как общетеоретический курс с ее практическими применениями в работе специалиста в области электроэнергетики и дать конкретный математический аппарат для прикладных исследований.
При изучении дисциплины рассматриваются математические методы и подходы для решения электроэнергетических задач.
Сложность задач электроэнергетики обусловлена:
-
сложностью ЭЭС, -
обеспечением надежной работы при различных авариях; -
высокой скоростью и взаимосвязью процессов, протекающих в различных элементах системы в нормальных и аварийных режимах.
-
Символический или комплексный метод расчета разветвленных электрических цепей переменного синусоидального тока средствами Matlab
-
Теоретические сведения
Метод контурных токов
При расчете методом контурных токов полагают, что в каждом независимом контуре течет свой контурный ток. Уравнения составляют относительно контурных токов, после чего определяют токи ветвей через контурные токи. Таким образом, число неизвестных в методе контурных токов определяется количеством независимых контуров и уравнения составляются по второму закону Кирхгофа. Этот метод является более экономичным с вычислительной точки зрения, т.к. содержит меньшее число уравнений. Покажем применение метода контурных токов на примере анализа следующей электрической цепи.
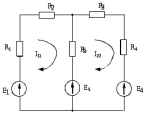
Рисунок 1.1 – Схема электрической цепи
В этой схеме два узла, три ветви и два независимых контура. Положим, что в левом контуре, по часовой стрелке, течет контурный ток
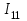 и в правом также по часовой стрелке течет контурный ток
и в правом также по часовой стрелке течет контурный ток 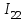 . Для каждого из контуров составим уравнения по второму закону Кирхгофа. При этом учтем, что в смежной ветви (с сопротивлением
. Для каждого из контуров составим уравнения по второму закону Кирхгофа. При этом учтем, что в смежной ветви (с сопротивлением 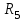 ) течет сверху вниз ток
) течет сверху вниз ток 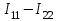 . Направление обхода контуров примем также по часовой стрелке.
. Направление обхода контуров примем также по часовой стрелке. Уравнение для первого контура по второму закону Кирхгофа:
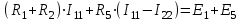 .
.Или, сгруппировав коэффициенты при неизвестных
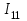 и
и 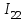 :
: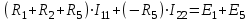 . (1.1)
. (1.1)Уравнения для второго контура:
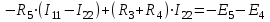 ,
,или
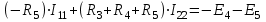 . (1.2)
. (1.2)В уравнении (1.1) коэффициент при неизвестном токе
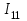 , являющийся суммой сопротивлений первого контура, обозначим через
, являющийся суммой сопротивлений первого контура, обозначим через 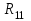 , коэффициент при токе
, коэффициент при токе 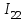 - сопротивление смежной ветви, взятое со знаком минус, обозначим через
- сопротивление смежной ветви, взятое со знаком минус, обозначим через 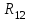 . Объединим эти уравнения в систему линейных алгебраических уравнений:
. Объединим эти уравнения в систему линейных алгебраических уравнений: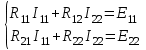 . (1.3)
. (1.3)Здесь:
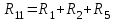 ,
,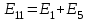 ,
,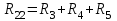 ,
,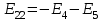 ,
,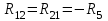 .
.В общем случае можно сказать, что сопротивление смежной ветви между
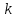 и
и 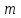
контурами (
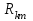 ) входит в уравнение со знаком минус, если направления контурных токов
) входит в уравнение со знаком минус, если направления контурных токов 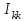 и
и 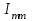 вдоль этой ветви встречны, и со знаком плюс, если направления согласны. Если в схеме будет больше двух контуров, например три, то система линейных алгебраических уравнений, составленных по второму закону Кирхгофа будет состоять из трех уравнений.
вдоль этой ветви встречны, и со знаком плюс, если направления согласны. Если в схеме будет больше двух контуров, например три, то система линейных алгебраических уравнений, составленных по второму закону Кирхгофа будет состоять из трех уравнений. В общем случае система для
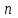 независимых контуров в матричной форме имеет следующий вид:
независимых контуров в матричной форме имеет следующий вид: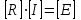 . (1.4)
. (1.4)Здесь матрица коэффициентов
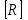 размерностью
размерностью 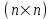 , Вектор столбец неизвестных
, Вектор столбец неизвестных 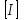 размерностью
размерностью 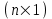 , столбец свободных членов
, столбец свободных членов 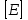 -
- 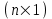 .
.Рекомендуется для единообразия в знаках сопротивлений с разными индексами все контурные токи направлять в одну и ту же сторону, например, все по часовой стрелке.
Если в результате решения системы линейных алгебраических уравнений какой-либо контурный ток окажется отрицательным, то это будет означать что в действительности направление контурного тока обратно, принятому, за положительное.
Квадратная матрица коэффициентов
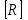 является симметричной матрицей относительно главной диагонали. Систему линейных алгебраических уравнений (1.4) можно решать каким-либо точным методом решения систем линейных алгебраических уравнений, например методом Гаусса (метод последовательных исключений), методом обратной матрицы, методом Крамера (метод определителей).
является симметричной матрицей относительно главной диагонали. Систему линейных алгебраических уравнений (1.4) можно решать каким-либо точным методом решения систем линейных алгебраических уравнений, например методом Гаусса (метод последовательных исключений), методом обратной матрицы, методом Крамера (метод определителей).Применение к анализу и расчету цепей переменного тока метода
 контурных токов.
контурных токов.Переменным током называется ток, изменяющийся во времени по величине и направлению. Значение тока в любой данный момент времени называется мгновенным значением тока
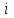 . Ток определен, если известна зависимость его мгновенного значения от времени
. Ток определен, если известна зависимость его мгновенного значения от времени 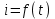 и указано его положительное направление. Токи, значения которых повторяются через равные промежутки времени в той же последовательности, называются периодическими.
и указано его положительное направление. Токи, значения которых повторяются через равные промежутки времени в той же последовательности, называются периодическими.Очень широкое распространение на практике получил символический, или комплексный метод расчета цепей синусоидального тока. Сущность символического метода расчета состоит в том, что при синусоидальном токе можно перейти от уравнений, составленных для мгновенных значений и являющихся дифференциальными уравнениями к алгебраическим уравнениям, составленным относительно комплексов тока и э.д.с. Этот переход основан на том, что в любом уравнении, составленном по законам Кирхгофа для установившегося процесса, мгновенное значение тока
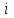 заменяют комплексной амплитудой тока
заменяют комплексной амплитудой тока 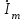 ; мгновенное значение напряжения на активном сопротивлении
; мгновенное значение напряжения на активном сопротивлении 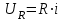 -комплексом
-комплексом 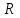
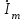 , мгновенное значение напряжения на индуктивности
, мгновенное значение напряжения на индуктивности 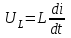 - комплексом
- комплексом 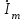
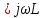 , опережающим ток на
, опережающим ток на 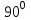 ; мгновенное значение напряжения на емкости
; мгновенное значение напряжения на емкости 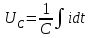 - комплексом
- комплексом 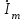
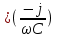 , отстающим от тока на
, отстающим от тока на 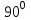 ; мгновенное значение э.д.с.
; мгновенное значение э.д.с. 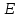 - комплексом
- комплексом 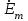 .
.Известно, что окончательные расчетные формулы метода контурных токов получают в результате выводов, в основу которых положен второй закон Кирхгофа. Поскольку первый и второй законы Кирхгофа справедливы и для цепей синусоидального тока, то все вышеприведенные выкладки справедливы и для цепей синусоидального тока. Все расчетные формулы пригодны и для расчета синусоидальных цепей, если в этих расчетных формулах вместо постоянного тока

