Файл: О. В. Свеженцева Подпись И. О. Фамилия пояснительная записка.docx

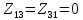– нет смежной ветви между первым и третьим контуром.

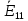- алгебраическая сумма э.д.с. первого контура: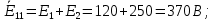



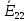- алгебраическая сумма э.д.с. второго контура: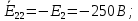



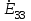- алгебраическая сумма э.д.с. третьего контура:



Следовательно, нахождение токов в схеме по методу контурных токов сводится к решению системы из трех линейных алгебраических уравнений с комплексными коэффициентами:

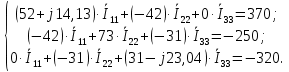
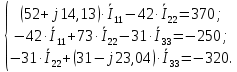
3. Решение задач линейной алгебры в системе MATLAB

>> Z=[52+i*14.13 -42 0;-42 73 -31;0 -31 31-i*23.04]
Z =
52.0000 +14.1300i -42.0000 0

-42.0000 73.0000 -31.0000

0 -31.0000 31.0000 -23.0400i
>> E=[370;-250;-320]
E =
370

-250

-320
>> I=Z\E
I =
0.5700 - 9.9004i

-4.7730 -12.0658i

-3.9474 -14.9997i

2. Решение систем обыкновенных дифференциальных уравнений в среде MATLAB

1. Теоретические сведения

Задачей Коши называется задача о решении обыкновенного дифференциального уравнения с известными начальными условиями. В MATLAB имеются три возможности для решения задачи Коши, не считая моделирования в SIMULINK.

Численные методы решения обыкновенных дифференциальных уравнений используются для расчета переходных процессов в электроэнергетических системах. Рекомендуемый численный метод расчета переходного процесса - метод Рунге-Кутта. Все изложение ведется под реализацию этого метода. Будем находить решение системы линейных дифференциальных уравнений.

В качестве исходных данных задачи имеем:

Систему обыкновенных дифференциальных уравнений 1-го порядка, описывающую переходный процесс в электроэнергетической системе.

Начальные условия Коши. Под начальными условиями Коши понимают значения искомых переменных при .

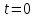Интервал интегрирования системы обыкновенных дифференциальных уравнений. Переходные процессы в линейных электрических цепях обычно являются быстропротекающими, длительность их составляет десятые, сотые доли секунды.

---

Должен быть задан шаг интегрирования 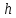. В MATLAB имеется несколько встроенных функций, которые позволяют решать задачу Коши для систем обыкновенных дифференциальных уравнений 1-го порядка.

Основная возможность – численное решение нелинейных дифференциальных уравнений с помощью команд типа ode23 и ode45. Буквенная часть названия этих команд – сокращение от Ordinary Differential Equation, цифры указывают порядок используемой версии метода Рунге–Кутты. Команда ode45 дает более точное решение, но требует больше времени.

1. Исходные данные

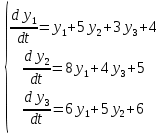
Начальные условия Коши:



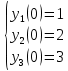
Интервал интегрирования
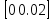
Для построения схемы решения системы уравнений в Simulink используется блок Integrator (класс Continuos). На его вход подается производная 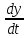, а на выходе имеем искомую функцию 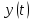. Блоки Gain (усилитель), блок Constant (константа), Sum (сумматор) используются для формирования правых частей системы обыкновенных дифференциальных уравнений.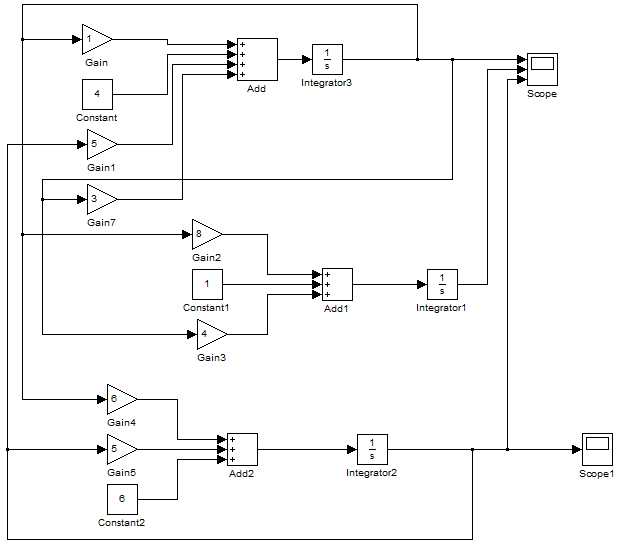



Рисунок 2.1 - Схема решения задачи в среде моделирования Simulink

2. Решение систем обыкновенных дифференциальных уравнений в системе MATLAB с помощью программного кода

Для проверки найденного решения создадим М-файл. В открывшемся окне создадим функцию, описывающую правые части системы дифференциальных уравнений.

function dy=vlm2(t,y)

dy=zeros(3,1);

dy(1)= y(1)+5*y(2)+3*y(3)+4;

dy(2)=8*y(1)+4*y(3)+5;

dy(3)=6*y(1)+5*y(2)+6;

После этого в командном окне наберем набор команд:

>> [T,Y]=ode45('vlm2',[0 0.02],[1 2 3])

>> plot(T,Y)

После этого появятся графики описывающие переходный процесс для 3-х переменных


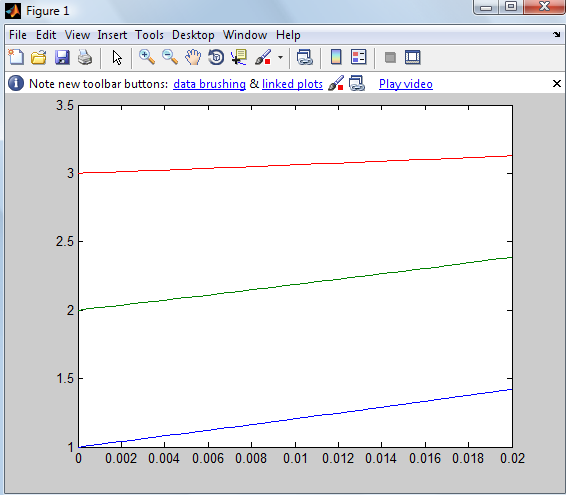
Рисунок 2.2 - График переходных процессов


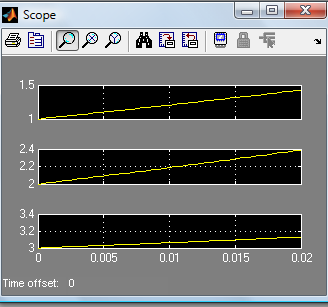
Рисунок 2.3 - Характеристики осциллографа в Simulink

Оба эти графических представления показывают идентичность найденных разными способами решений.

---

3. Аппроксимация таблично заданной функции в средеMATLAB

1. Теоретические сведения

Рассчитать и построить аппроксимирующую характеристику повторяемости скоростей ветра по многолетним данным фактических наблюдений. Многолетние данные представлены в виде гистограммы повторяемости скоростей ветра в заданном диапазоне скоростей. Для аппроксимации использовать двухпараметрическое распределение Вейбулла, имеющее следующее выражение:



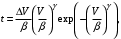
где: t – вероятность появления текущей скорости ветра; 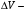интервал градаций скоростей ветра; V – текущая скорость ветра в интервале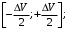 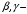параметры распределения Вейбулла.

Исходными данными для расчета является гистограмма (частость) скорости ветра в заданном интервале скоростей ветра, регламентированных нормативными документами по обработке фактических данных наблюдений, получаемых с метеорологических станций.
Регламентированные интервалы скоростей ветра, в которых определяется частость появления скоростей по данным многолетних наблюдений, м/с:

0-1; 2-3; 4-5; 6-7; 8-9; 10-11; 12-13; 14-15; 16-17; 18-20; 21-24; 25-28; 29-34; 35-40.

Средние значения скорости ветра в интервале, м/с:

0,5; 2,5; 4,5; 6,5; 8,5; 10,5; 12,5; 14,5; 16,5; 19; 22,5; 26,5; 31,5; 27,5.

Фактическая повторяемость скоростей ветра задается в справочных данных по каждому месяцу года в виде следующей таблицы:

Таблица 3.1 - Повторяемость скоростей ветра в году

Града-ции скоро-стей	0-1	2-3	4-5	6-7	8-9	10-11	12-13	14-15	16-17	18-20	21-24	25-28	29-34	35-40
Повторяемо-сть,%	35,5	28,1	17,0	6,19	3,1	2,77	1,78	1,44	1,19	1,76	0,76	0,42	0,19	0,2

---

Задача аппроксимации состоит в том, чтобы гистограмму повторяемости скоростей ветра, являющейся дискретной функцией от скорости ветра (повторяемость задана постоянным значением в интервале скоростей ветра), превратить в непрерывную функцию вероятности появления скоростей ветра для любого заданного значения скорости ветра V.

Для определения параметров уравнения Вейбулла β, γ, аппроксимирующего фактические данные повторяемости, используются следующие расчетные соотношения:



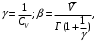
где: 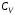- коэффициент вариации; 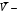среднее значение скорости ветра в интервале; Г(x) –гамма функция интегральное преобразование, определяемое выражением: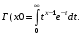



Коэффициент вариации подсчитывается по выражению:



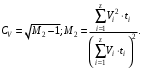
В выражениях для коэффициента вариации: М₂ – относительный начальный момент второй степени; z – число градаций скоростей ветра, при которых фактическая повторяемость больше нуля.

Задачей расчета является вычисление М₂, С_V, а затем β и γ с использованием языка MATLAB, позволяющего выполнять операции с векторами.

2. Исходные данные

Для метеостанции BG-4 «Б.Гол.» в апреле месяце фактическая повторяемость скоростей ветра составляет:

Таблица 3.2 - Исходные данные

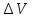,м/с	0-1	2-3	4-5	6-7	8-9	10-11	12-13	14-15	16-17	18-20
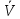, м/с	0,5	2,5	4,5	6,5	8,5	10,5	12,5	14,5	16,5	19
t,%о	224	263	249	152	63	33	13	4	1	0

---

В таблице 3.2: – интервалы градаций скоростей ветра, м/с;

– средняя скорость в интервале, м/с;

t,%о - повторяемость скоростей ветра в интервале в процентилях (тысячных процентах).

В результате расчетов получаем:

М₂ =1.53 – относительный начальный момент второй степени:


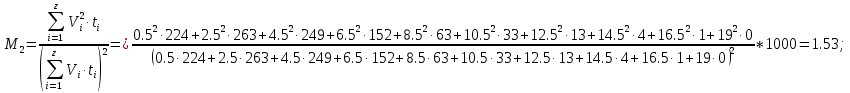
С_V = 0.73 – коэффициент вариации;


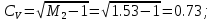
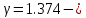параметр уравнения Вейбулла;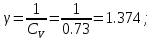


Г = 1.73 – функции от аргумента (1+1/ γ) в ;



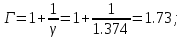
Для определения β предварительно потребовалось рассчитать значение Г – функции от аргумента (1+1/ γ) =1,73, которое определялось в MATLAB, задав команду gamma(1.73).

β = 4,3695 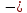параметр уравнения Вейбулла.
Кроме аппроксимации фактических данных следует определить среднегодовую энергию ветра по формуле:





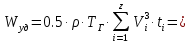
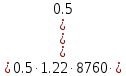
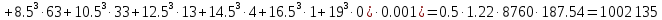Вт/(м²·год);

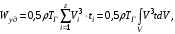Вт/(м²·год),

где ρ = 1,22 кг/м2 – плотность воздуха; Т_Г – число часов в году.
Составим MATLAB программу для расчета необходимых параметров задачи и сравним полученные результаты.

>> v=[0.5 2.5 4.5 6.5 8.5 10.5 12.5 14.5 16.5 19]
v =
Columns 1 through 8
0.5000 2.5000 4.5000 6.5000 8.5000 10.5000 12.5000 14.5000
Columns 9 through 10
16.5000 19.0000
>> t=[224 263 249 152 63 33 13 4 1 0]
t =
224 263 249 152 63 33 13 4 1 0
>> a=v*(t')*0.001
a =
3.9970
>> b=(v.^2)*(t')*0.001
b =
24.4985
>> m=b/(a^2)
m =
1.5335
>> Cv=sqrt(m-1)
Cv =
0.7304
>> gamma=1/Cv
gamma =
1.3691
>> GF=Gamma(1+1/gamma)
GF =
0.9147
>> beta=a/GF
beta =
4.3695
>> v=0.5:0.1:19
v =
Columns 1 through 8
0.5000 0.6000 0.7000 0.8000 0.9000 1.0000 1.1000 1.2000
Columns 9 through 16
1.3000 1.4000 1.5000 1.6000 1.7000 1.8000 1.9000 2.0000
Columns 17 through 24
2.1000 2.2000 2.3000 2.4000 2.5000 2.6000 2.7000 2.8000
Columns 25 through 32
2.9000 3.0000 3.1000 3.2000 3.3000 3.4000 3.5000 3.6000
Columns 33 through 40
3.7000 3.8000 3.9000 4.0000 4.1000 4.2000 4.3000 4.4000
Columns 41 through 48
4.5000 4.6000 4.7000 4.8000 4.9000 5.0000 5.1000 5.2000
Columns 49 through 56
5.3000 5.4000 5.5000 5.6000 5.7000 5.8000 5.9000 6.0000
Columns 57 through 64
6.1000 6.2000 6.3000 6.4000 6.5000 6.6000 6.7000 6.8000

---