Федеральное агентство связи

Сибирский Государственный Университет Телекоммуникаций и Информатики

Межрегиональный центр переподготовки специалистов

КОНТРОЛЬНАЯ РАБОТА

По дисциплине: Теория телетрафика

Вариант: 05

Проверил: Лизнева Ю. С.

Новосибирск, 2016 г.

Задача 1. На коммутационную систему поступает поток вызовов, создающий нагрузку Y эрланг. Определить вероятности поступления ровно i вызовов P_i (i=0, 1, 2 ...N) при примитивном потоке от N источников и P_i ( i=0,1, 2...j...) при простейшем потоке вызовов. Построить кривые распределения вероятностей P_i =f ( i ) и произвести сравнение полученных результатов. Величины Y и N приведены в табл. 1.

Таблица 1

Номер варианта	5
Y, эрл	2,1
N	6

Дано:

Y = 2,1 эрл

N = 6

Решение:

Вероятностный процесс поступления вызовов простейшего потока описывается формулой (распределения) Пуассона:



















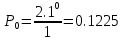
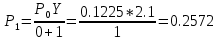
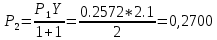
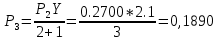
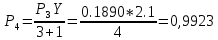
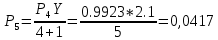
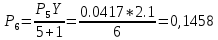
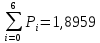
Нагрузка, поступающая от одного источника



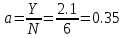
Вероятность поступления i вызовов при примитивном потоке

или 

---

.

















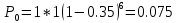
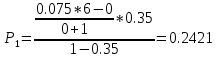
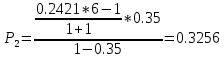
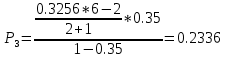
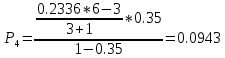
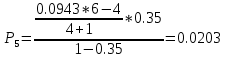
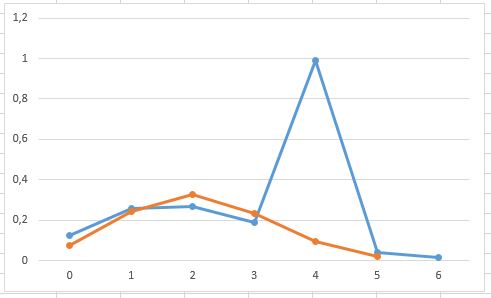
Кривые распределения вероятностей

Задача 2. Пучок ИШК координатной станции типа АТСК -Y обслуживает абонентов одного блока АИ. Определить поступающую на этот пучок нагрузку Y, если число абонентов, включенных в блок, N=1000, среднее число вызовов от одного абонента С, среднее время разговора Т , доля вызовов закончившихся разговором P_P . значения с, Т и P_P приведены в таблице 2 . нумерация на сети пяти- или шестизначная.

Таблица 2.

Номер варианта	5
c, выз/час	2,4
T, c	130
PP	0,55

Дано:

С – 2,4 выз/час

Т - 130 с

Рр - 0,55

N - 1000

Решение:

Величина интенсивности нагрузки рассчитывается по формуле:

.

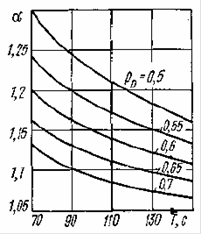
Коэффициент α определим по графику



Величина

p=tc.o.+tc+tп.в.+Т+to,

где: tc.o.=2,4 c. - средняя продолжительность слушания абонентом сигнала «ответ станции»; tc=1,5m+2,8 - средняя продолжительность установления соединения (m - число знаков абонентского номера); tп.в.=7÷8 с. - средняя продолжительность посылки вызова; t0≈0 - продолжительность освобождения приборов АТС.

p=2,4+(1,5*5+2,8)+7.+100+0=119,7 с=0,033час.

Тогда:

Y= 1,15*1000*2,4*0,03*0,55 = 45,54 эрл

Задача 3. Полнодоступный пучок из V линий обслуживает поток вызовов. Определить пропускную способность пучка, т.е. нагрузку Y , которая может поступать на этот пучок при заданной величине потерь по вызовам P

---

_В

в случае простейшего потока и примитивного потока от N₁ и N₂ источников. Значения V, P_B, N₁ и N₂ приведены в таблице 3. По результатам расчета сделать выводы.

Таблица 3

Номер варианта	5
V	5
PB,%0	2
N1	20
N2	10

Дано:

V - 5

Рв - 2%

N1 – 20

N2 - 10

Решение:

Для простейшего потока значение Y определяем из таблицы приложения 1, расчитаной по формуле Эрланга

Для V = 5, Pв = 2 %0 пропускная способность полнодоступного пучка линий обслуживающего простейший поток вызовов составит Y = 0.9 Эрл.

Для примитивного потока значение Y определяем из таблицы приложения 2, расчитаной по формуле Энгсета.

Для N1 = 20, V = 5, Pв = 2 % а =0,05 Эрл. Отсюда, Y1=aN=1 Эрл.

Для N2 = 10, V = 2, Pв = 2 % а = 0,12 Эрл. Тогда, Y2=1.2 Эрл.

Полученные результаты показывают, чем меньше число источников нагрузки в случае примитивного потока, тем больше пропускная способность. С уменьшением числа источников нагрузки пропускная способность увеличивается и наоборот. Если неограниченно увеличивать число источников нагрузки, то примитивный поток будет стремиться к простейшему.

Задача 4.На коммутационный блок координатной станции типа АТСК поступает простейший поток вызовов, который создает нагрузку Y_б эрланг при средней длительности занятия входа блока t_б . Блок обслуживается одним маркером, работающим в режиме с условными потерями при постоянной длительности занятия t_м. Блок обслуживается одним маркером, работающем в режиме с условными потерями при постоянной длительности занятия t_{м .}

Задержанные вызовы обслуживаются в случайном порядке независимо от очередности поступления.

Определить вероятность ожидания свыше допустимого времени t_д и среднее время ожидания задержанных вызовов t_{з .} Значения Y_б , t_б, t_м и t_{д .}

приведены в табл. 4.

Таблица 4

Номер варианта	5
Yб, эрл	24
tб,с	48
tм,с	0,2
tд ,с	0,3

---

Дано:

Y_б - 24 эрл

t_б - 48 с

t_м – 0,2 с

t_д  -0,3 с

Процесс обслуживания маркером поступающих вызовов можно рассматривать как математическую модель обслуживания простейшего потока, работающим по системе с ожиданием при выборке вызовов из очереди. Качественные показатели модели зависят от дисциплины выбора вызова из очереди на обслуживание. Они могут быть следующими:

в порядке поступления (в порядке очереди);

в случайном порядке.

Эта модель исследована Берком. Результаты Берка нашли применение при расчете качественных показателей работы управляющих устройств (маркеров) в координатных системах АТС. В итоге работы Берка были построены кривые. Эти кривые дают возможность легко определить значения требуемых величин: вероятность ожидания свыше времени t, т.е. Р (g>t) и среднее время ожидания tз в зависимости от нагрузки на маркер

Для определения величины нагрузки на маркер Yм воспользуемся формулой:



Подставляя числовые значения, получим:

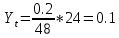Эрл.

Нагрузка поступающая на маркер меньше 1 Эрл., следовательно, маркер с такой нагрузкой справится. Допустимое время ожидания выражается соотношением:



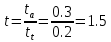
По графикам приложения 3 [2] определим Р (g>t) и gз.

Р (g>t) = 0,003, gз = 0,48. Тогда среднее время ожидания задержанных вызовов равно:

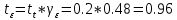с
Задача 5.Нагрузка, поступающая на ступень ГИ АТСК, обслуживается в данном направлении пучком линий с доступностью K_Bq при потерях P=0,005. Нагрузка на один вход ступени а, нагрузка в направлении y . Определить методом эффективной доступности емкость пучка V при установке на ступени блоков 60х80х400 и 80х120х400. Сравнить полученные результаты. Величины

K_Bq , y, a приведены в таблице 5.

Таблица 5

Номер варианта	5
KBq	20
y, Эрл	32
а, Эрл	0,41

Дано:

Кв q - 20

y - 32 Эрл

а - 0,41 Эрл

---

Р - 0,005

Решение:

Блок 60х80х400.

Структурные параметры блока: A= 15 - число входов 1 коммутатора; A = 20 - число выходов 1 коммутатора (mA = kв = 20).= 1 - число ПЛ, соединяющих два коммутатора на соседних звеньях (связность).

Метод эффективной доступности используется как для полнодоступных, так и неполнодоступных схем. Он основан на понятии переменной доступности, которая зависит от числа занятых линий.

Минимальная доступность равна:

dmin = (m - n + 1) q

= 1 - число выходов из коммутатора последнего звена, которое объединяется в рассматриваемом направлении.

dmin = (20 - 15 + 1) 1 = 6

Определим среднюю доступность:



m - нагрузка, обслуживаемая m выходами одного коммутатора первого звена. Эту величину приближенно можно определить как

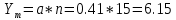Эрл.

Тогда,



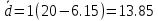
Так как идея метода эффективной доступности заключается в замене 2-хзвенной КС на однозвенную неполнодоступную с такой же пропускной способностью, поэтому рассчитаем однозвенную неполнодоступную КС с такой же пропускной способностью. Доступность такой схемы называется эффективной и равна:



- коэффициент, зависящий от зависимости потерь от доступности и распределения доступности. Для режима группового искания значение коэффициента  можно принять равным 0,75.



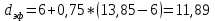
Требуемое количество линий равно:



у - нагрузка, поступающая в рассматриваемом направлении.

---

Смотрите также файлы

• Алексеевских Олеся Владимировна Алексеевских Олеся Владимировна.docx

• Панорамалы саба бта даярлау тжірибем.pptx

• Практическая работа 6 Определение налогооблагаемой базы и расчет суммы налога с оборота, подлежащей уплате в бюджет..docx

• Традиционные и современные оздоровительные системы физических упражнений.docx

• Лабораторная работа 1 Исследование резисторного каскада предварительного усиления на биполярном транзисторе.doc