ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 12
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вариант 14
| № предприятия п/п | Темп обновления основных фондов Y | Уровень травматизма, чел. в год X1 | Средний возраст работающего Х2 | % рабочих, состоящих в профсоюзе Х3 |
| 1 | 1,8 | 16 | 49,0 | 71 |
| 2 | 1,6 | 44 | 20,0 | 67 |
| 3 | 1,8 | 13 | 31,9 | 72 |
| 4 | 2,7 | 12 | 33,4 | 71 |
| 5 | 2,1 | 12 | 35,3 | 72 |
| 6 | 1,0 | 18 | 24,6 | 73 |
| 7 | 2,0 | 22 | 30,8 | 73 |
| 8 | 0,9 | 9 | 43,4 | 78 |
| 9 | 1,9 | 10 | 42,4 | 72 |
| 10 | 1,0 | 7 | 53,8 | 77 |
| 11 | 1,5 | 7 | 60,6 | 76 |
| 12 | 1,7 | 6 | 58,1 | 77 |
| 13 | 3,5 | 8 | 61,1 | 77 |
| 14 | 1,4 | 6 | 70,2 | 77 |
| 15 | 0,4 | 7 | 73,7 | 78 |
| 16 | 1,0 | 6 | 78,3 | 78 |
| 17 | 0,1 | 5 | 65,8 | 76 |
| 18 | 1,3 | 5 | 85,1 | 79 |
| 19 | 0,3 | 4 | 68,7 | 79 |
| 20 | 0,6 | 6 | 73,9 | 78 |
Бланк выполнения задания 2
| № п/п | Пункт исследования | Ответ |
| 1. | Постройте линейную модель множественной регрессии. | 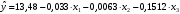 |
| 2. | Запишите стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжируйте факторы по степени их влияния на результат. | 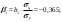 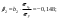 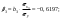 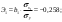 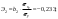 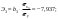 Ранжирование (от min. до max): β2; β1; β3; Ранжирование (от min. до max): Э2; Э1; Э3. |
| 3. | Найдите коэффициенты парной, частной и множественной корреляции. Проанализируйте их. | 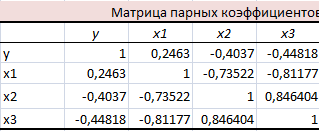 Анализ матрицы коэффициентов парной корреляции начнем с анализа первого столбца матрицы, в котором расположены коэффициенты корреляции, отражающие тесноту связи, зависимой переменной темпа обновления основных фондов с факторами включенными в модель. Анализ показывает, что зависимая переменная, то есть темп обновления основных фондов, имеет обратную, заметную связь с % рабочих, состоящих в профсоюзе (ryx3 = - 0,448) и с средним возрастом работающего (ryx2 = - 0,404), слабую, прямую связь с уровнем травматизма (ryx1 = 0,246. 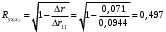 Коэффициент множественной корреляции указывает на умеренную связь всего набора факторов с результатом. |
| 4. | Найдите скорректированный коэффициент множественной детерминации. Сравните его с нескорректированным (общим) коэффициентом детерминации. | 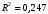 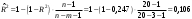 Оба коэффициента указывают на заметную (более 20%) детерминированность результата 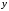 в модели факторами в модели факторами |
| 5. | С помощью F – критерия Фишера оцените статистическую надежность уравнения регрессии и коэффициента детерминации Ryx1x22 | 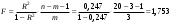 Получили, что  (при (при 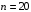 ), т.е. вероятность случайно получить такое значение ), т.е. вероятность случайно получить такое значение 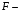 критерия не превышает допустимый уровень значимости 5%. Следовательно, полученное значение случайно, оно сформировалось под влиянием не существенных факторов, т.е. подтверждается статистическая не значимость всего уравнения и показателя тесноты связи критерия не превышает допустимый уровень значимости 5%. Следовательно, полученное значение случайно, оно сформировалось под влиянием не существенных факторов, т.е. подтверждается статистическая не значимость всего уравнения и показателя тесноты связи 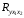 . . |
| 6. | С помощью частных F –критериев Фишера оцените целесообразность включения в уравнение множественной регрессии фактора х1 после х2 и фактора х2 после х1 | 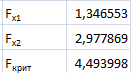 Получили, что 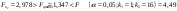 Следовательно, включение в модель фактора Следовательно, включение в модель фактора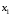 после того, как в модель включен фактор после того, как в модель включен фактор 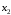 статистически нецелесообразно: прирост факторной дисперсии за счет дополнительного признака статистически нецелесообразно: прирост факторной дисперсии за счет дополнительного признака 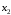 оказывается оказываетсянезначительным, несущественным; фактор 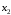 включать в уравнение после фактора включать в уравнение после фактора 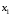 не следует. не следует. |
| 7. | Составьте уравнение линейной парной регрессии, оставив лишь один значащий фактор | 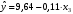 |

