Файл: Лекция Освоение детьми количественных отношений, чисел и цифр.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 44
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рис. 2.
Как же ведут себя дети при наличии множества, расположенного не линейно, а в виде числовой фигуры? Дети до трех лёт почти не принимают этого задания, если даже инструкция сопровождается показом того, как надо делать. Часть детей трех лет все же пытается подложить пуговицы, но делает это своеобразно: они выкладывают пуговицы вокруг всей карточки, при этом тесно прижимают их друг к другу (рис. 3). Между тем почти все дети владели приемом наложения.
Рис. 3.
Следует отметить, что малышей затрудняет не только сам прием, но и смысл слов подложить, приложить (некоторые дети прятали взятые ими пуговицы под карточку). Отсюда следует вывод, что детям второго и третьего года жизни необходимо практически разъяснять различия смысла слов наложить, приложить, подложить.
Рис. 4 Рис. 5
Даже старшие дети (пять лет), выполняя задание уложить на полоске столько пуговиц, сколько их было в числовой фигуре, раскладывают их или вокруг четырех сторон квадрата, или вокруг трех сторон, или по двум сторонам, или конструируют форму числовой фигуры прямо на столе, причем не в равном количестве (рис. 4 и 5). Внимание детей сосредоточивается на самом способе нового действия приложения, а восприятие количества вытесняется.
В чем же общая причина затруднений в овладении способом приложения элементов одного множества к элементам другого и почему именно этот способ является наиболее значимым в формировании количественного восприятия множества?
Чтобы подложить в совокупности пуговиц одну пуговицу под другой, необходимо дифференцировать пространственные отношения между всеми элементами множества, точно воспринять их количество как при линейном расположении, так и в виде числовой фигуры.
Почему же дети сравнительно легко овладевают приемом наложения при восприятии тех же множеств? Решая задание способом наложения, ребенок накладывает пуговицу на ее изображение, закрывает ее, и ведущими для него являются сами изображения; пространственные же отношения между нарисованными пуговицами не играют в решении данного задания еще существенной роли, и ребенок не замечает их. Ему важно последовательно закрыть все рисунки совокупности. Таким образом, прием наложения способствует, с одной стороны, формированию представления о множестве как структурно замкнутом целом, а с другой — усиливает внимание детей к тому, что множество состоит из отдельных элементов. Общее же количество элементов еще мало интересует ребенка.
В чем же причина затруднений при подкладывании элементов, какие новые задачи возникают перед ребенком при овладении данным способом? Ребенку надо точно воспроизвести то количество элементов, которое образует данное множество. Для этого необходимо воспринять не только изображения пуговиц, но и пространственные отношения между ними. Только при этом условии можно выделить количественную сторону множества. Учитывать же расстояния между изображениями ребенок еще не научился. Если при наложении ребенок руководствуется самим изображением, то для использования приема приложения он должен подняться на новый уровень восприятия множества — научиться видеть пространственные отношения между рисунками, т. е. элементами внутри множества, что подведет его к точному количественному их восприятию.
Не владея еще умением анализировать пространственные отношения между элементами как при линейном их расположении, так и в числовой фигуре, ребенок заполняет площадь в границах множества, тесно прижимая пуговицы друг к другу, а тем самым воспроизводит неадекватное образцу количество. И если в процессе обучения на пространственную дифференцировку элементов внутри множества не обращается должного внимания, то отсутствие такой дифференцировки влечет за собой значительные ошибки в восприятии количественной стороны совокупности даже на том этапе, когда ребенок, казалось бы, научился считать с помощью слов-числительных. Приведем один из многочисленных примеров такого поведения.
Юра П. 5 лет 1 мес. Юра свободно называет числительные до 13. На предложенной карточке он считает семь пуговиц, расположенных в ряд, затем отсчитывает пуговицы по одной, укладывая их в ряд на нижней полоске, не руководствуясь, однако, тем, чтобы пуговицы точно располагались под их рисунками 1:1. Положив шесть пуговиц, Юра останавливается, считая задание законченным, поскольку он заполнил, как ему кажется, всю площадь в границах множества. Когда по просьбе воспитательницы он пересчитывает оба множества, то обнаруживает свою ошибку, так как не слышит соответствия при назывании последних числительных в обоих множествах. В процессе пересчитывания Юра случайно несколько отодвинул пуговицы. Увидев свободное место под последней пуговицей образца, он еще теснее сдвинул их и добавил еще две пуговицы. Уже по собственной инициативе Юра пересчитал снова обе совокупности и вновь убедился в том, что сделал неверно. «Не так»,— говорит Юра. Он вновь еще теснее сдвигает пуговицы, добавляя одну. На образце семь пуговиц, а у него девять. Пересчитав снова, говорит: «Неверно у меня. Не получается что-то, еще передвинуть надо». Сдвинув еще теснее, он добавил еще одну, десятую, пуговицу и вновь убедился, что сделал неверно. «Что-то опять не получается. Вот работу потруднее дали. Но ведь получится как-то». Попытку помочь Юра решительно отверг: «Я сам. Потруднее работу дали, чтобы гадать. Как же это?» — раздумывает Юра. «А ты попробуй наложить пуговицы на кружки»,—советует все же педагог. Юра воспользовался советом. «Семь! — обрадовался он.— Вот сколько лишних я взял. Не получилось. Лишние пуговицы были».
Таким образом, только при наводящем указании Юра смог сопоставить элементы одного множества с элементами другого, один к одному.
Выполняя задание воспроизвести множество, расположенное в виде числовой фигуры, и трансфигурировать его линейно, Юра сосчитал на карточке пять пуговиц затем взял пуговицы по одной, не считая, и разложил по две пуговицы по трем сторонам квадрата: верхней, правой и нижней. Юра внимательно смотрит на выложенные им пуговицы, сопоставляет их одна с другой, рассуждает при этом вслух: «Эта к этой, эта не к этой идет, а к этой» и т. д., потом снимает одну пуговицу и пересчитывает оба множества. Но он не слышит при счете в последних называемых числительных соответствия. «Как же это правильно сделать?» Вновь сопоставляет элементы один к одному. «Эта к этой, эта к этой (пауза), так, эта не к этой идет, а к этой»,— рассуждает вслух Юра. Вновь все считает и радостно заявляет: «Здесь пять и здесь пять, теперь верно».
Итак, Юра не усвоил еще подлинного значения счета; он знает лишь одно: равенство множеств бывает тогда, когда последние числительные при их назывании совпадают, а когда он не слышит этого совпадения, считает, что допустил какую-то ошибку, но в чем она состоит, для него остается неясным. Это можно продемонстрировать еще на одном примере.
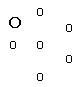
Рис. 6.
Юра считает семь кружков, выложенных на карточке, как показано на рис. 6, и ошибается, говоря «шесть». «Ты неверно считал».— «Нет, все верно»,— возражает Юра, однако вновь пересчитывает: «Ой, нет, не все верно. Семь». Юра начинает раскладывать пуговицы вокруг формы, но педагог напоминает ему, что надо раскладывать в ряд. Юра кладет пуговицы одна за другой, называя числительные, но считает не пуговицы, а свои движения. Например, положив четвертую пуговицу в ряд, говорит «пять», так как, взяв ее из коробки, сказал «четыре». Выложив еще одну пуговицу и назвав число шесть, Юра говорит: «Все», считая задание выполненным; он уже забыл количество пуговиц на карточке. «Посчитай, верно ли ты положил». Юра считает кружки на карточке, но пропускает один и говорит, что кружков шесть. Снова пересчитав, он находит, что их семь: «Семь, а эту я забыл. Ой, чего это я все забываю!» Еще раз считает рисунки пуговиц и убеждается, что их семь. «Семь»,— утверждает он и начинает считать выложенные им пуговицы. «Шесть,— говорит он,— опять неверно». Подумав, добавляет одну пуговицу и заявляет довольный: «Теперь уже семь. Вот какую трудную задачу даете».
На что же следует обратить особое внимание, анализируя поведение детей? Счетом дети пользуются не как средством определения количества элементов множества: называя числительные по порядку, они ждут, когда появится в этой цепочке слово-числительное, то, которое будет соответствовать по звучанию числительному, названному при счете другой совокупности. Тем самым число для этих детей не является еще показателем количества элементов множества. Констатируя при пересчитывании двух множеств их несоответствие, дети обнаруживают его лишь по разноименному звучанию последних слов-числительных. Дети эти не владеют еще в подлинном смысле деятельностью счета как деятельностью установления взаимно-однозначного соответствия между предметами и числами натурального ряда. Они легко сбиваются при счете, небрежно соотносят слова-числительные с объектами совокупности: то пропускают слова-числительные, то пропускают объекты при счете, то сразу называют два числительных, соотнеся с ними один объект. Дети, казалось бы, проявляют активность в счете, однако они еще не поднялись до уровня понимания значения счета.
Приведенный пример свидетельствует, что дети преждевременно перешли к счетной деятельности с помощью слов-числительных. У них не сформировалось еще четкое восприятие всех элементов множества. Они не научились практически сравнивать множества, сопоставляя их элементы один к одному. Отсутствие этих знаний не позволило им четко усвоить операцию счета «..подняться к более глубокому пониманию значения числа как показателя равночисленности множеств. Естественно, что для этих детей остается неясным и значение последовательности чисел, которую они легко нарушают, поскольку запоминание порядка слов-числительных у них сформировалось лишь на основе речедвигательных ассоциаций.
Приведенные факты свидетельствуют об огромной важности и значении формирования представлений о множестве и о различных операциях с множествами еще в дочисловой период обучения.
Отсюда следует сделать вывод: необходимо уже с раннего возраста не только учить детей различать «много и один», но и формировать представление о множестве как структурно-целостном единстве, а также четкое восприятие отдельных элементов, образующих множество. Все это и будет подводить ребенка к умению считать элементы множества с помощью слов-числительных. Предварительная работа с множествами позволит детям в последующем скорее и глубже осмыслить понятие числа и овладеть деятельностью счета.
Значение операций с множествами в дочисловой период
Уже в дочисловой период могут проводиться с множествами различные операции с множествами. Выше указывалось на тенденцию восприятия детьми множества как единого целого, если все его элементы качественно однородны. Если такая тенденция является вполне оправданной в период перехода от восприятия множественности к восприятию множества как структурно-целостного единства (в 2—4 года), то позднее она становится препятствием к дальнейшему развитию. Например, на столе лежат четыре рыбки и в коробке — шесть рыбок. Ребенок шести лет воспринимает их только раздельно. На вопрос, сколько всего рыбок, он отвечает, что, если из коробки выложить на стол и остальные рыбки, их будет десять. Или другой пример: девочка нарисовала по обе стороны реки по два домика. На вопрос, сколько всего домиков по обе стороны реки, она ответила: если эти два домика перенести на другую сторону, тогда их будет четыре.
Различное пространственное расположение элементов множества мешает восприятию их в единстве.
Поэтому необходимо предлагать детям производить различные операции с множествами: составлять единое множество из двух групп, каждая из которых обладает своими качественными особенностями, несущественными для всего множества в целом. Например, объединить несколько красных и синих флажков в единое множество флажков или, наоборот, разделить единое множество (кружков) на подмножества по тому или иному признаку (цвета, размера, формы, вида и др.). Таким образом, одно и то же множество, составленное по родовому признаку, может быть упорядочено в подмножества по разным признакам. И все эти выделенные подмножества могут сопоставляться, сравниваться друг с другом, при этом выявляться количественные отношения между ними, равенства, неравенства, не выражаемые еще числом.
Обследования, проведенные среди первоклассников, показали, что далеко не все дети, перешедшие из детского сада в школу, умеют упорядочивать множества по разным признакам, понимать различные отношения между ними.
Из этого вытекает следующий вывод: на протяжении всего дошкольного возраста необходимо работать с детьми над множествами. Особое внимание уделять формированию представлений о множестве как структурно-целостном единстве и в то же время учить видеть каждый отдельный элемент множества. При этом нет необходимости спешить обучать детей счету с помощью слов-числительных. Значительно важнее научить детей приемам поэлементного сравнения двух множеств, установления соответствия между их элементами. В среднем и старшем дошкольном возрасте целесообразно обучать различным операциям с множествами, учить сравнивать множества, обладающие разными качественными признаками, видеть равенство и неравенство множеств как практически (вне счета), так и обучая счету с помощью слов-числительных.

