Файл: Решение. 1 В табл. 10. 1 представлен ранжированный ряд 1.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.03.2024
Просмотров: 12
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Произвести статистическую обработку массива из n = 30 данных, содержащихся в столбцах №2, №3 и №4 таблицы 1.
Таблица 1
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10
__________________________________________________________
561 555 569 555 567 559 567 555 566 557
580 568 560 572 563 574 542 562 542 572
564 560 569 543 560 565 568 558 539 550
566 563 562 546 570 582 568 565 561 554
548 558 586 562 559 553 567 553 572 567
550 562 557 564 582 576 567 554 567 550
534 574 560 561 578 543 544 567 576 550
567 546 571 570 560 546 566 578 581 555
576 572 542 567 566 548 578 539 550 551
556 540 557 548 540 577 576 548 553 573
и выполнить следующие задания:
1) составить ранжированный ряд, найти размах выборки и количество групп различных вариант;
2) составить точечный вариационный ряд;
3) преобразовать точечный вариационный ряд в интервальный с числом интервалов k = 8;
4) построить полигон относительных частот и гистограмму;
5) найти статистические характеристики выборки;
6) проверить гипотезу о нормальном распределении генеральной совокупности с помощью критерия Пирсона при числе степеней свободы s = 5 и уровне значимости α = 0,05;
7) найти доверительный интервал для математического ожидания генеральной совокупности с надежностью γ = 0,95.
Решение. 1) В табл.10.1 представлен ранжированный ряд:
Таблица 10.1
| 540 | 542 | 543 | 546 | 546 | 548 | 555 | 555 | 557 | 557 |
| 558 | 560 | 560 | 560 | 561 | 562 | 562 | 562 | 563 | 564 |
| 567 | 568 | 569 | 569 | 570 | 571 | 572 | 572 | 574 | 586 |
Размах R = 586 – 540 = 46; различных групп m = 21
-
Точечный вариационный ряд представим в виде табл.10.2 с указанием номера группы
Таблица 10.2
| № | xi | ni | Wi |
| 1 | 540 | 1 | 0,03333 |
| 2 | 542 | 1 | 0,03333 |
| 3 | 543 | 1 | 0,03333 |
| 4 | 546 | 2 | 0,06667 |
| 5 | 548 | 1 | 0,03333 |
| 6 | 555 | 2 | 0,06667 |
| 7 | 557 | 2 | 0,06667 |
| 8 | 558 | 1 | 0,03333 |
| 9 | 560 | 3 | 0,1 |
| 10 | 561 | 1 | 0,03333 |
| 11 | 562 | 3 | 0,1 |
| 12 | 563 | 1 | 0,03333 |
| 13 | 564 | 1 | 0,03333 |
| 14 | 567 | 1 | 0,03333 |
| 15 | 568 | 1 | 0,03333 |
| 16 | 569 | 2 | 0,06667 |
| 17 | 570 | 1 | 0,03333 |
| 18 | 571 | 1 | 0,03333 |
| 19 | 572 | 2 | 0,06667 |
| 20 | 574 | 1 | 0,03333 |
| 21 | 586 | 1 | 0,03333 |
| Итого | | 30 | 1 |
-
Находим длину интервала h = 46/8 = 5,75 и формируем табл.10.3
Таблица 10.3
| № интервала | Границы интервала | ni | Wi | ni/h |
| 1 | 540,0 - 545,75 | 3,00 | 0,1 | 0,522 |
| 2 | 545,75 - 551,5 | 3,00 | 0,1 | 0,522 |
| 3 | 551,5 - 557,25 | 4,00 | 0,133 | 0,696 |
| 4 | 557,25 - 563,0 | 8,00 | 0,2667 | 1,391 |
| 5 | 563,0 - 568,75 | 4,00 | 0,133 | 0,696 |
| 6 | 568,75 - 574,5 | 7,00 | 0,233 | 1,217 |
| 7 | 574,5 - 580,25 | 0,00 | 0 | 0 |
| 8 | 580,25 - 586,0 | 1,00 | 0,033 | 0,174 |
| | | 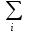 ni = 30 ni = 30 | 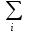 Wi = 1. Wi = 1. | |
-
По данным табл.10.2 строим полигон относительных частот, который представлен на рис.10.1:
Р
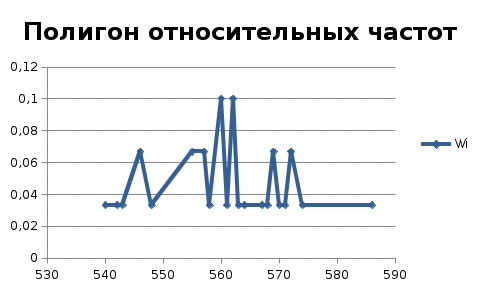 ис.10.1
ис.10.1П
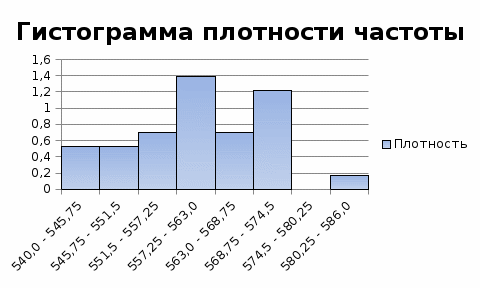 о данным табл.3 строим гистограмму плотности частоты, представленной на рис.10.2:
о данным табл.3 строим гистограмму плотности частоты, представленной на рис.10.2:Рис.10.2
5) Находим статистические характеристики выборки:
Моды М(Х) = 560 и М(Х) = 562; медиана Ме(Х)= (561 + 562)/2 = 561,5; выборочные: средняя
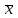
= 560,7; дисперсия
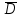 = 99,959; среднее квадратичное отклонение
= 99,959; среднее квадратичное отклонение 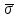 = 9,998. Как видно коэффициент вариации (
= 9,998. Как видно коэффициент вариации (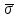 /
/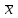 ) не превосходит 2%, что свидетельствует о том, что данные выборки не выходят за пределы первого класса точности расчетов.
) не превосходит 2%, что свидетельствует о том, что данные выборки не выходят за пределы первого класса точности расчетов.6) Находим для аргумента z функции Лапласа границы интервалов (zi, zi+1) в виде: zi = ( хi -
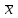 )/
)/ 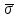 , zi+1 = ( хi+1 -
, zi+1 = ( хi+1 - 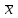 )/
)/ 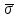 и заполняем табл.10.4
и заполняем табл.10.4Таблица 10.4
| № | Границы интервалов Х | Границы интервалов z |
| хi хi+1 | zi zi+1 | |
| 1 | 540,0 545,75 | - ∞ -1,470 |
| 2 | 545,75 541,5 | -1,470 -0,905 |
| 3 | 551,5 557,25 | -0,905 -0,339 |
| 4 | 557,25 563,0 | -0,339 0,226 |
| 5 | 563,0 568,75 | 0,226 0,792 |
| 6 | 568,75 574,5 | 0,792 1,357 |
| 7 | 574,5 580,25 | 1,357 1,923 |
| 8 | 580,25 586,0 | 1,923 +∞ |
Находим теоретические вероятности pi и теоретические частоты niт = npi, заполняя табл.10.5
Таблица 10.5
| № | z | Ф(z) | pi | niт |
| zi zi+1 | Ф(zi) Ф(zi+1) | |||
| 1 | - ∞ -1,470 | -0,5 -0,43 | 0,0487 | 1,461 |
| 2 | -1,470 -0,905 | -0,43 -0,32 | 0,112 | 3,36 |
| 3 | -0,905 -0,339 | -0,32 -0,13 | 0,1855 | 5,565 |
| 4 | -0,339 0,226 | -0,13 0,09 | 0,2241 | 6,723 |
| 5 | 0,226 0,792 | 0,09 0,29 | 0,1971 | 5,913 |
| 6 | 0,792 1,357 | 0,29 0,41 | 0,125 | 3,75 |
| 7 | 1,357 1,923 | 0,41 0,47 | 0,0601 | 1,803 |
| 8 | 1,923 +∞ | 0,47 0,50 | 0,0206 | 0,618 |
Σ = 1 30
Вычисляем χ2набл , для чего формируем табл.10.6:
Таблица 10.6
| № | ni | niт | (ni - niт)2/niт | ni2/niт |
| 1 | 3 | 1,461 | 1,621 | 6,160 |
| 2 | 3 | 3,36 | 0,039 | 2,679 |
| 3 | 4 | 5,565 | 0,440 | 2,875 |
| 4 | 8 | 6,723 | 0,243 | 9,520 |
| 5 | 4 | 5,913 | 0,619 | 2,706 |
| 6 | 7 | 3,75 | 2,817 | 13,067 |
| 7 | 0 | 1,803 | 1,803 | 0,000 |
| 8 | 1 | 0,618 | 0,236 | 1,618 |
Σ = 7,817 38,624
Таким образом, χ2набл = 7,817. По таблицам критических точек χ2 при числе степеней свободы s = 5 и уровне значимости α = 0,05 определяем χ2кр =11,1 и, следовательно, имеем χ2набл < χ2кр.
Вывод 1. Расхождение эмпирических и теоретических частот случайно (не значительно) и нулевую гипотезу о нормальном распределении генеральной совокупности принимаем.
7) Из соотношения 2Ф(t) = 0,95 по таблицам Лапласа находим аргумент t = 1,96. Тогда точность оценки при n = 30 и

