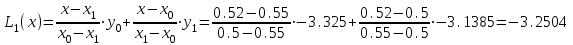Лабораторная работа №2

по теме «Интерполяция функций»

1. Вопросы, подлежащие изучению

1. 
   Постановка задачи аппроксимации и интерполяции. Интерполяция в точке. Погрешность интерполяции.
   
2. 
   Основные понятия: интерполирующая и интерполируемая функции, условие интерполяции. Связь между числом узлов интерполяции и порядком интерполирующего полинома.
   
3. 
   Интерполяционный полином Лагранжа: назначение, область применения.
   
4. 
   Интерполяционная формула Ньютона, область применения.
   
5. 
   Конечные разности, их назначение и использование. Свойства конечных разностей
   
6. 
   Методика выбора узлов интерполяции при использовании формул Лагранжа и Ньютона.
   
7. 
   Способы оценки погрешностей интерполяции по формулам Лагранжа и Ньютона. Способы повышения точности интерполяции.
   

2. 
   Задание
   

В этой лабораторной работе решается задача интерполяции в точке путем построения семейства интерполяционных полиномов разных степеней с оценкой погрешности полученных решений.

1. 
   Выбрать из таблицы 1–1 индивидуальное задание для интерполяции:
   

• 
  точку интерполяции x=b для интерполяции полиномом Лагранжа;
  
• 
  точку интерполяции x=a для интерполяции полиномом Ньютона;
  

1. 
   Выполнить вручную интерполяцию в заданной точке x=b с использованием полинома Лагранжа 1–й, 2–й и 3–й степени:
   

• 
  выбрать из таблицы 1–2 с интерполируемой функцией четыре подходящих узла. Перенумеровать узлы и занести перенумерованные узлы в таблицы вида 1–3.
  
• 
  записать интерполяционные формулы для 1, 2 и 3-ей степени полинома;
  
• 
  выполнить расчеты по интерполяционным формулам для каждой степени полинома; все промежуточные вычисления производить с сохранением всех значащих цифр, окончательные результаты округлять до 4 знаков после десятичной точки.
  
• 
  занести полученные результаты в таблицу вида 1–4;
  
• 
  вычислить оценки погрешности в точке b для полиномов различных степеней и занести их в таблицу 1-4.
  

---

1. 
   Выполнить вручную интерполяцию в заданной точке x=a с использованием полинома Ньютона 1–й, 2–й и 3–й степени:
   

• 
  выбрать из таблицы 1–2 с интерполируемой функцией четыре подходящих узла. Перенумеровать узлы и занести перенумерованные узлы в таблицы вида 1–3.
  
• 
  заполнить таблицу конечных разностей (для интерполяционной формулы Ньютона);
  
• 
  записать интерполяционные формулы для 1, 2 и 3-ей степени полинома;
  
• 
  выполнить расчеты по интерполяционным формулам для каждой степени полинома; все промежуточные вычисления производить с сохранением всех значащих цифр, окончательные результаты округлять до 4 знаков после десятичной точки.
  
• 
  занести полученные результаты в таблицу вида 1–5;
  
• 
  вычислить оценки погрешности в точке а для полиномов различных степеней и занести их в таблицу 1-5.
  

4. 
   Объяснить полученные результаты и сделать выводы.
   

1.3. Варианты задания для ручного расчета и таблица интерполируемой функции

Таблица 1–1

№ варианта	Полином Ньютона x=a	Полином Лагранжа x=b
1	0.06	0.43
2	0.11	0.72
3	0.16	1.17
4	0.21	0.58
5	0.31	0.12
6	0.36	1.21
7	0.41	1.46
8	0.46	0.87
9	0.51	0.48
10	0.61	1.37
11	0.07	0.51
12	0.12	0.96
13	0.17	0.64
14	0.22	1.52
15	0.32	0.77
16	0.37	0.17
17	0.42	1.02
18	0.52	0.34
19	0.62	1.41
20	0.08	0.23
21	0.13	0.67
22	0.17	1.29
23	0.23	0.81
24	0.32	1.26
25	0.42	1.12
26	0.47	0.93
27	0.53	0.37
28	0.63	0.26
29	0.09	1.07
30	0.14	1.33

---

Таблица 1–2

№ узла	Значение аргумента xi	Значение функцииyi
0	0.05	-4.1710
1	0.10	-4.1330
2	0.15	-4.0845
3	0.20	-4.0240
4	0.25	-3.9500
5	0.30	-3.8610
6	0.35	-3.7555
7	0.40	-3.6320
8	0.45	-3.4890
9	0.50	-3.3250
10	0.55	-3.1385
11	0.60	-2.9280
12	0.65	-2.6920
13	0.70	-2.4290
14	0.75	-2.1375
15	0.80	-1.8160
16	0.85	-1.4630
17	0.90	-1.0770
18	0.95	-0.6565
19	1.00	-0.2000
20	1.05	0.2940
21	1.10	0.8270
22	1.15	1.4005
23	1.20	2.0160
24	1.25	2.6750
25	1.30	3.3790
26	1.35	4.1295
27	1.40	4.9280
28	1.45	5.7760
29	1.50	6.6750
30	1.55	7.6265

---

1.4. Формы таблиц для занесения результатов

Таблица 1–3

k	0	1	2	…	n
xk	x0	x1	x2	…	xn
yk	y0	y1	y2	…	yn

Таблица 1-4

(для полинома Лагранжа)

Степень многочлена k	Lk(x)	Погрешность
1	L1(x)	|L1(x) – L2(x)|
2	L2(x)	|L2(x) – L3(x)|
3	L3(x)	–

Таблица 1–5

(для полинома Ньютона)

Степень многочлена k	Pk(x)	Погрешность
1	P1(x)	|P1(x) – P2(x)|
2	P2(x)	|P2(x) – P3(x)|
3	P3(x)	–

---

1.5. Содержание отчета

1. Фамилия и имя студента, номер группы.

2. Название и цель лабораторной работы.

3. Индивидуальный вариант задания к работе.

4. Таблицы 1–3 с перенумерованными узлами интерполяции.

5. Интерполяционные формулы для ручных расчетов и результаты расчетов в таблицах 1–4 и 1-5.

6. Выводы.

1.6. Пример выполнения задания

1. 
   Точка интерполяции для формулы Лагранжа b = 0.52.
   

Выбор и перенумерация узлов.

Для ручной интерполяции в точке x = b = 0.52 по формуле Лагранжа выбираем из таблицы 1–2 4 узла так, чтобы точка b = 0.52 оказалась внутри получающийся таблицы и узлы были наиболее близкими к этой точке. В итоге выбираем узлы с номерами 8, 9, 10, 11:

8	0.45	-3.4890
9	0.50	-3.3250
10	0.55	-3.1385
11	0.60	-2.9280

Следует отметить, что формула Лагранжа может использоваться как для таблиц с постоянным шагом, так и с непостоянным шагом. Перенумеруем узлы интерполяции руководствуясь двумя правилами: точка x=b должна быть внутри таблицы и узлы должны быть ближайшие к ней. Занесем перенумерованные узлы в таблицу вида 1–3:

k	0	1	2	3
xk	0.50	0.55	0.45	0.60
yk	-3.3250	-3.1385	-3.4890	-2.9280

Ручной расчет по формуле Лагранжа.

Запишем интерполяционные полиномы Лагранжа 1–й, 2–й и 3–й степени и вычислим их значения в точке x = b = 0.52:

---

Смотрите также файлы

• Тема арматура и основные узлы контактной сети и воздушных линий.ppt

• 6 пай 2 ні кез келген натурал мнінде рнегі 19а блінетінін длелде. 4 пай.doc

• Лекций 2 и 3.docx

• Земля наш дом. Словообразование и орфография.docx

• Обучение пациента с неосложненной формой хронического бронхита Мендыбаева Гульнара.pptx