Файл: Лабораторная работа 1 По дисциплине Вычислительная техника и информационные технологии Выполнил Группа.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.03.2024
Просмотров: 16
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Федеральное агентство связи
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
Лабораторная работа №1
По дисциплине: Вычислительная техника и информационные технологии
Выполнил:
Группа:
Вариант: 1
Проверил: Чухров А.С.
Исследование логических схем на элементах «И–НЕ»
Цель работы:
Изучение свойств логических элементов «И–НЕ»; приобретение навыков синтеза логических схем.
Задание к лабораторной работе:
Экспериментально исследовать правила построения различных логических функций в базисе И-НЕ, снять таблицы истинности для указанных выше логических функций.
Ход работы:
1. Логическая функция «НЕ»
Схема лабораторной установки для реализации логической функции «НЕ» представлена на рисунке1.,сигнал подается на входы 2,3:
На входе 1 уровень «0»,на входе 4-«1»:
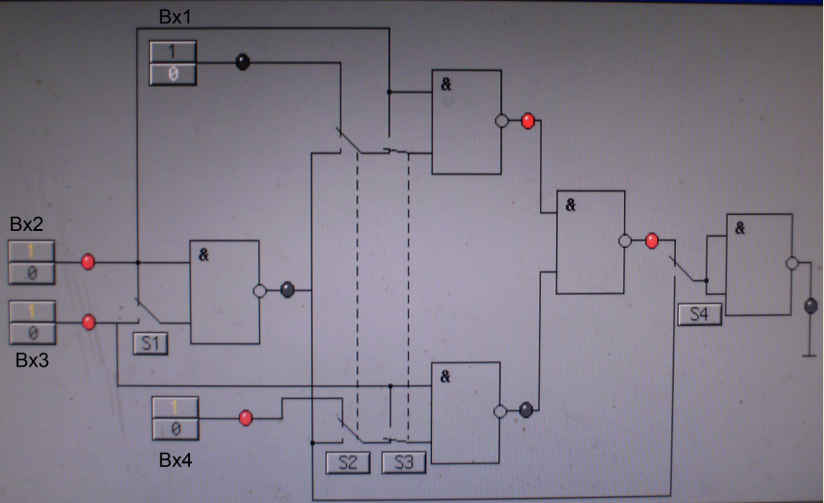
Рис 1
Логическая функция «НЕ»
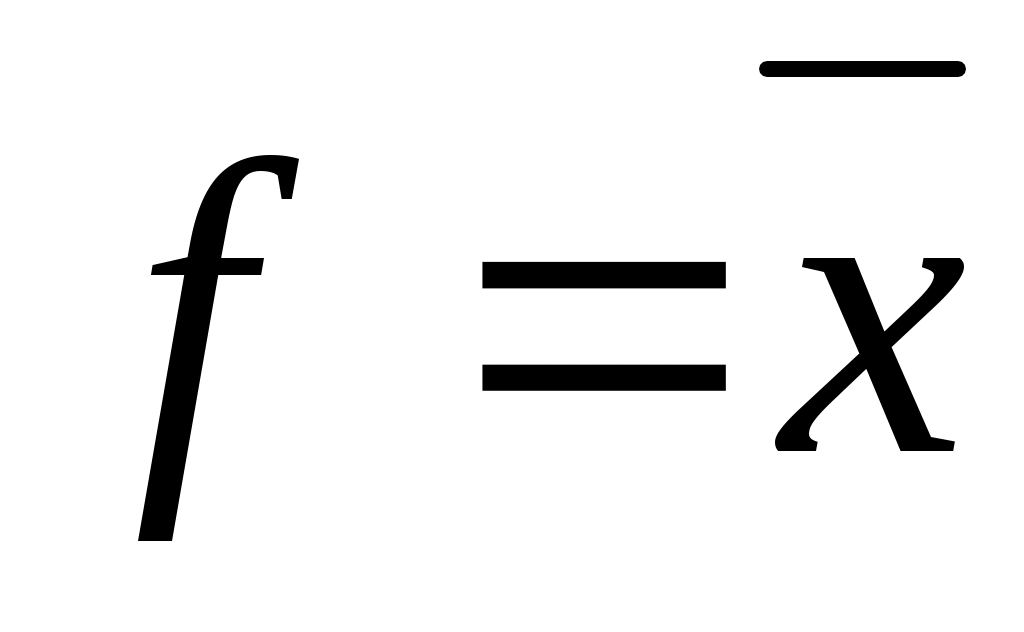
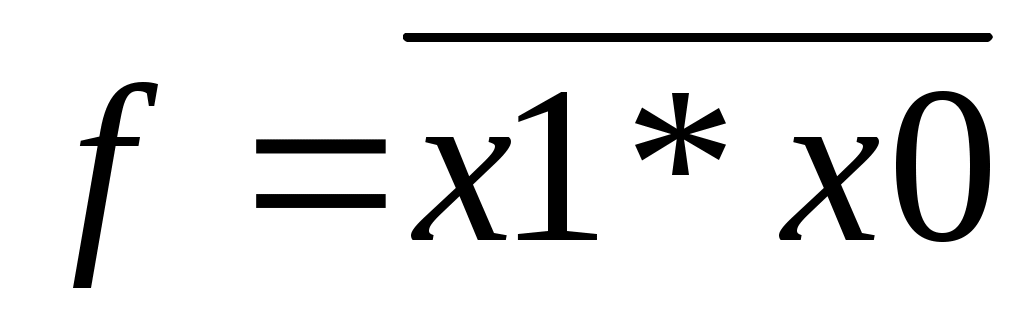
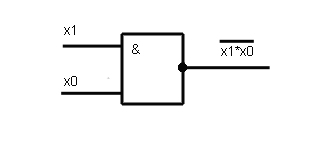
Рис2
Таблица истинности:
-
i
1
2
3
4
x1
0
1
0
1
x0
0
0
1
1
Y
f1
f2
f3
f4
1
1
0
0
Таблица 1
2. Логическая функция «ИЛИ»
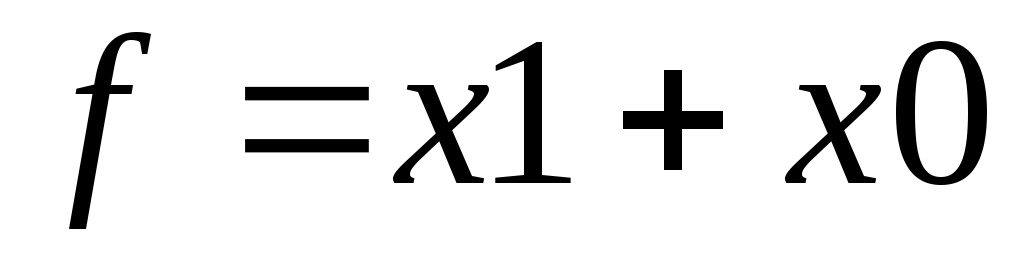
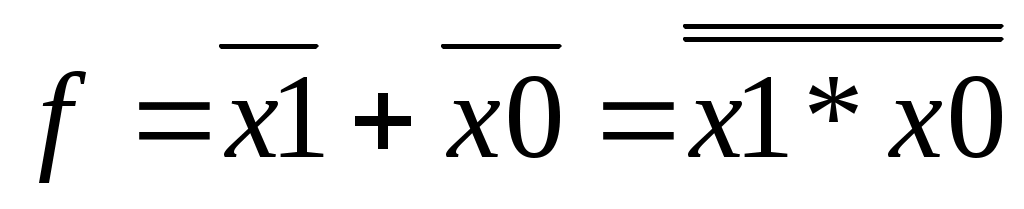
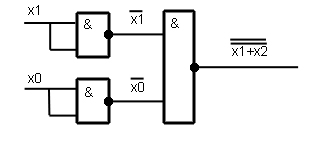
Рис 3.
Таблица истинности:
Федеральное агентство связи
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
Лабораторная работа №1
По дисциплине: Вычислительная техника и информационные технологии
Выполнил:
Группа:
Вариант: 1
Проверил: Чухров А.С.
Исследование логических схем на элементах «И–НЕ»
Цель работы:
Изучение свойств логических элементов «И–НЕ»; приобретение навыков синтеза логических схем.
Задание к лабораторной работе:
Экспериментально исследовать правила построения различных логических функций в базисе И-НЕ, снять таблицы истинности для указанных выше логических функций.
Ход работы:
1. Логическая функция «НЕ»
Схема лабораторной установки для реализации логической функции «НЕ» представлена на рисунке1.,сигнал подается на входы 2,3:
На входе 1 уровень «0»,на входе 4-«1»:

Рис 1
Логическая функция «НЕ»
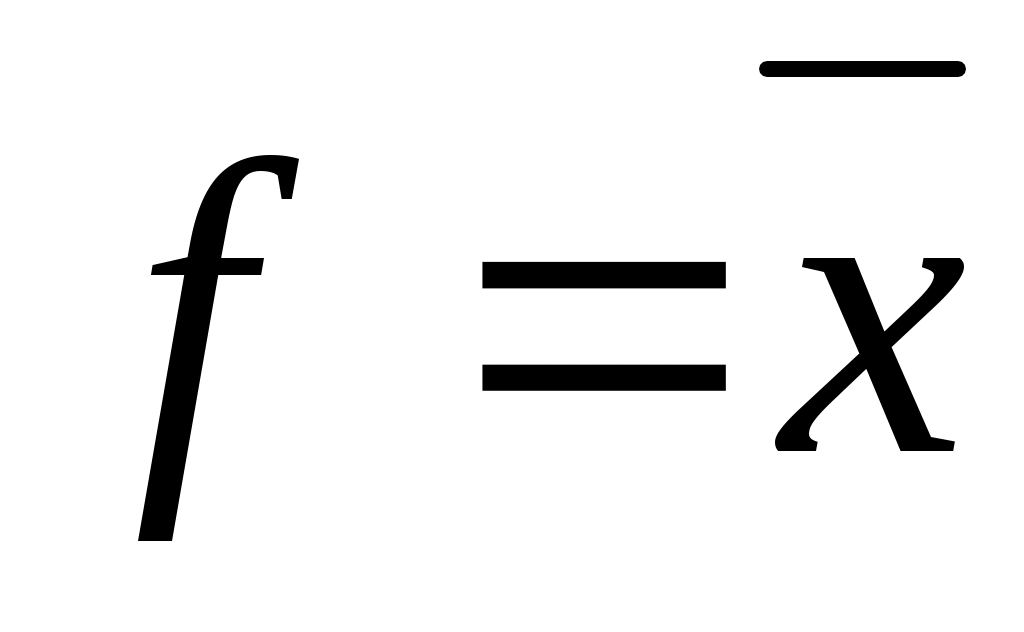
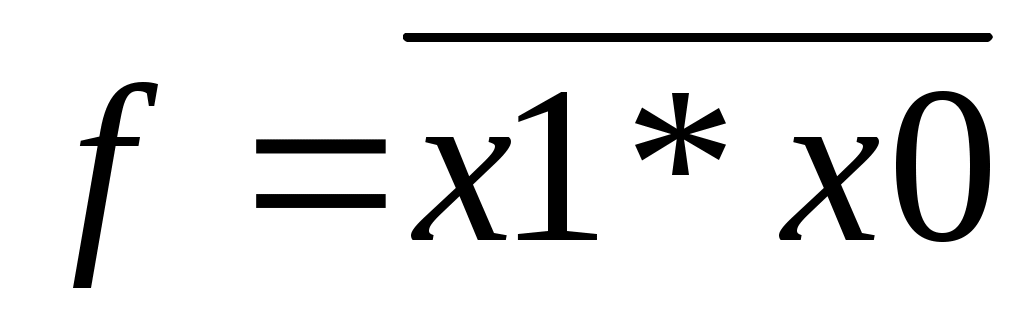

Рис2
Таблица истинности:
-
i
1
2
3
4
x1
0
1
0
1
x0
0
0
1
1
Y
f1
f2
f3
f4
1
1
0
0
Таблица 1
2. Логическая функция «ИЛИ»
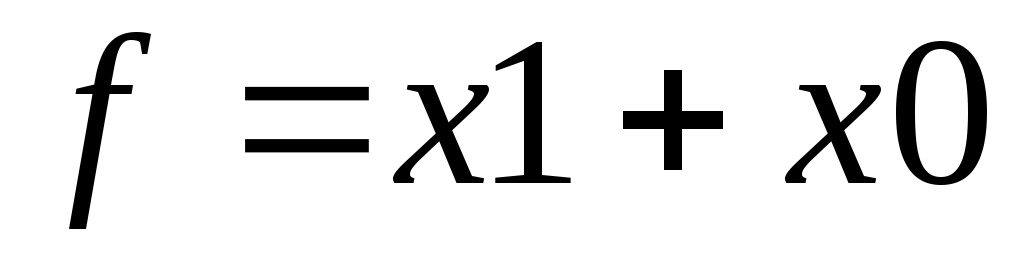
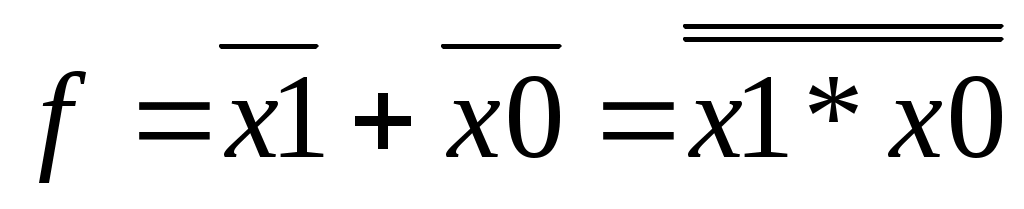

Рис 3.
Таблица истинности:
Федеральное агентство связи
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
Лабораторная работа №1
По дисциплине: Вычислительная техника и информационные технологии
Выполнил:
Группа:
Вариант: 1
Проверил: Чухров А.С.
Исследование логических схем на элементах «И–НЕ»
Цель работы:
Изучение свойств логических элементов «И–НЕ»; приобретение навыков синтеза логических схем.
Задание к лабораторной работе:
Экспериментально исследовать правила построения различных логических функций в базисе И-НЕ, снять таблицы истинности для указанных выше логических функций.
Ход работы:
1. Логическая функция «НЕ»
Схема лабораторной установки для реализации логической функции «НЕ» представлена на рисунке1.,сигнал подается на входы 2,3:
На входе 1 уровень «0»,на входе 4-«1»:

Рис 1
Логическая функция «НЕ»
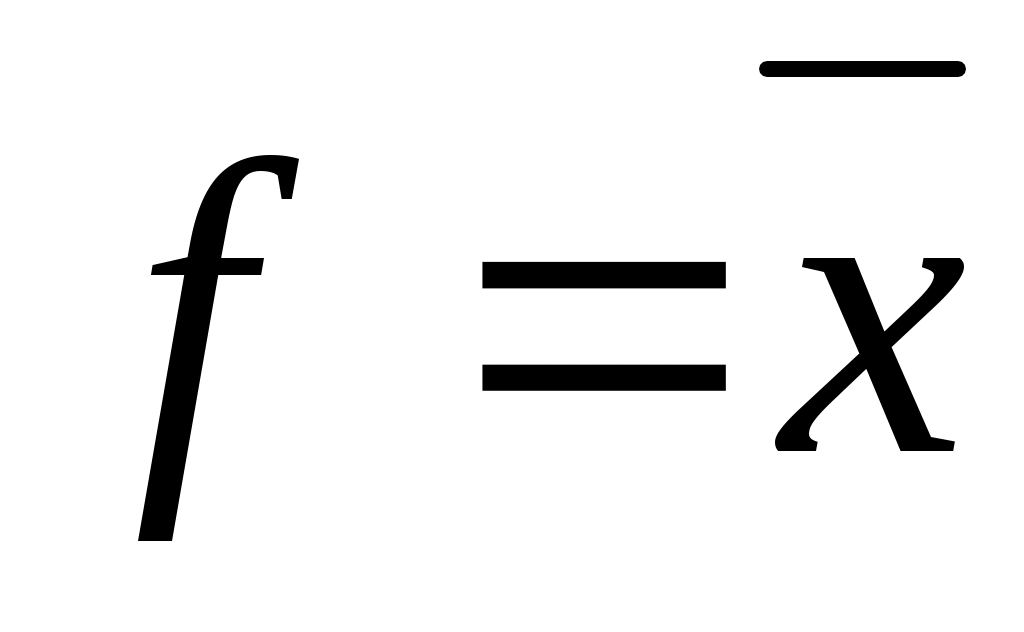
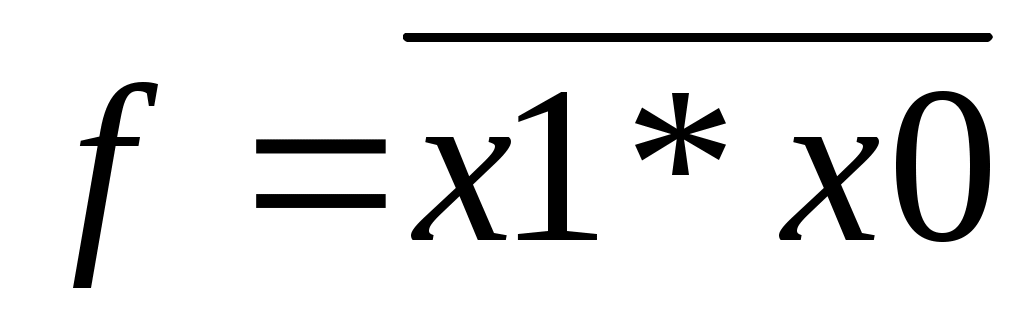

Рис2
Таблица истинности:
-
i
1
2
3
4
x1
0
1
0
1
x0
0
0
1
1
Y
f1
f2
f3
f4
1
1
0
0
Таблица 1
2. Логическая функция «ИЛИ»
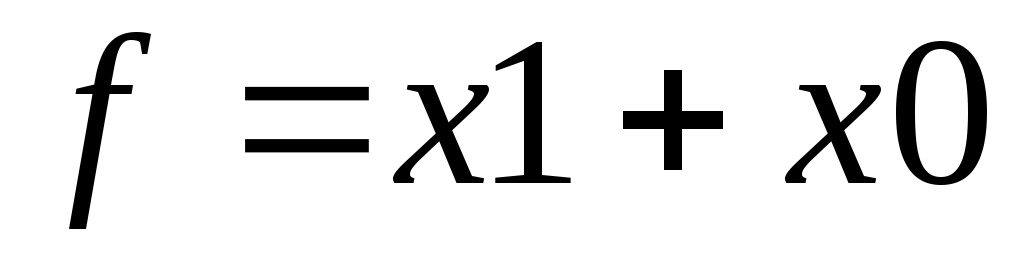
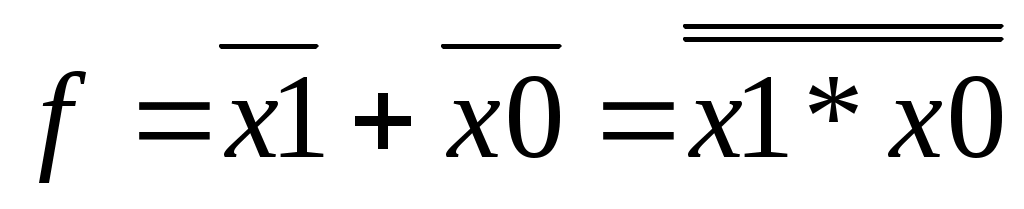

Рис 3.
Таблица истинности:
Федеральное агентство связи
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
Лабораторная работа №1
По дисциплине: Вычислительная техника и информационные технологии
Выполнил:
Группа:
Вариант: 1
Проверил: Чухров А.С.
Исследование логических схем на элементах «И–НЕ»
Цель работы:
Изучение свойств логических элементов «И–НЕ»; приобретение навыков синтеза логических схем.
Задание к лабораторной работе:
Экспериментально исследовать правила построения различных логических функций в базисе И-НЕ, снять таблицы истинности для указанных выше логических функций.
Ход работы:
1. Логическая функция «НЕ»
Схема лабораторной установки для реализации логической функции «НЕ» представлена на рисунке1.,сигнал подается на входы 2,3:
На входе 1 уровень «0»,на входе 4-«1»:

Рис 1
Логическая функция «НЕ»
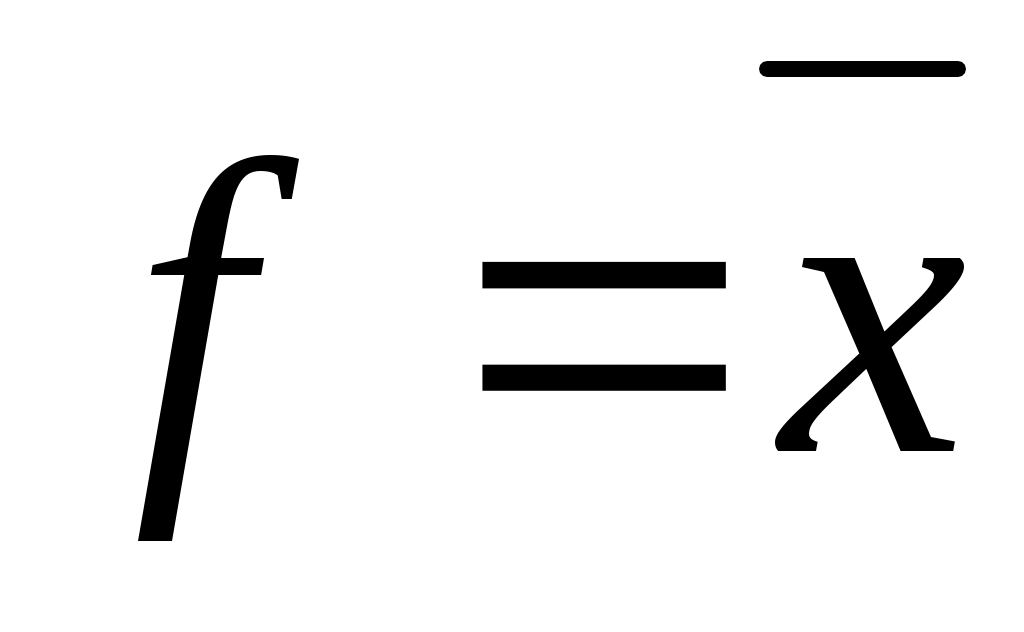
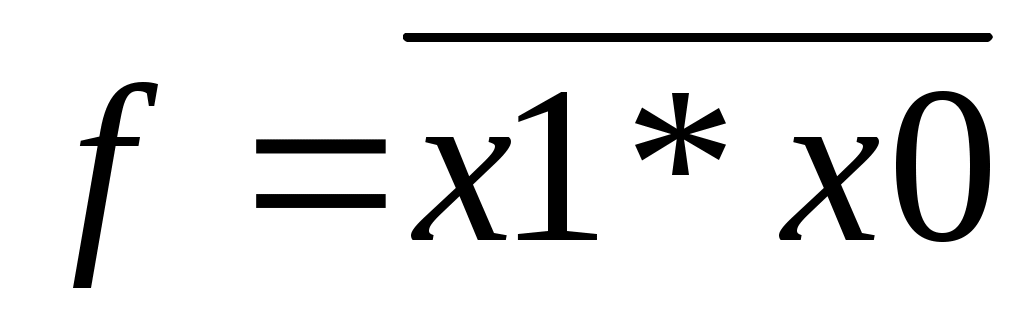

Рис2
Таблица истинности:
-
i
1
2
3
4
x1
0
1
0
1
x0
0
0
1
1
Y
f1
f2
f3
f4
1
1
0
0
Таблица 1
2. Логическая функция «ИЛИ»
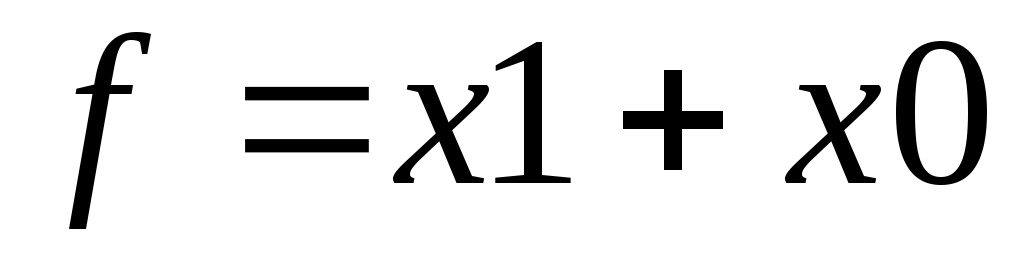
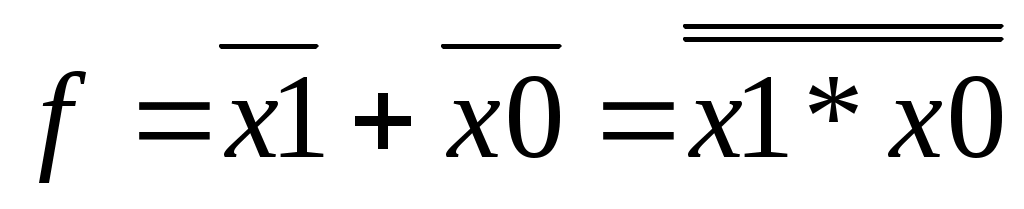

Рис 3.
Таблица истинности:
Федеральное агентство связи
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
Лабораторная работа №1
По дисциплине: Вычислительная техника и информационные технологии
Выполнил:
Группа:
Вариант: 1
Проверил: Чухров А.С.
Исследование логических схем на элементах «И–НЕ»
Цель работы:
Изучение свойств логических элементов «И–НЕ»; приобретение навыков синтеза логических схем.
Задание к лабораторной работе:
Экспериментально исследовать правила построения различных логических функций в базисе И-НЕ, снять таблицы истинности для указанных выше логических функций.
Ход работы:
1. Логическая функция «НЕ»
Схема лабораторной установки для реализации логической функции «НЕ» представлена на рисунке1.,сигнал подается на входы 2,3:
На входе 1 уровень «0»,на входе 4-«1»:

Рис 1
Логическая функция «НЕ»
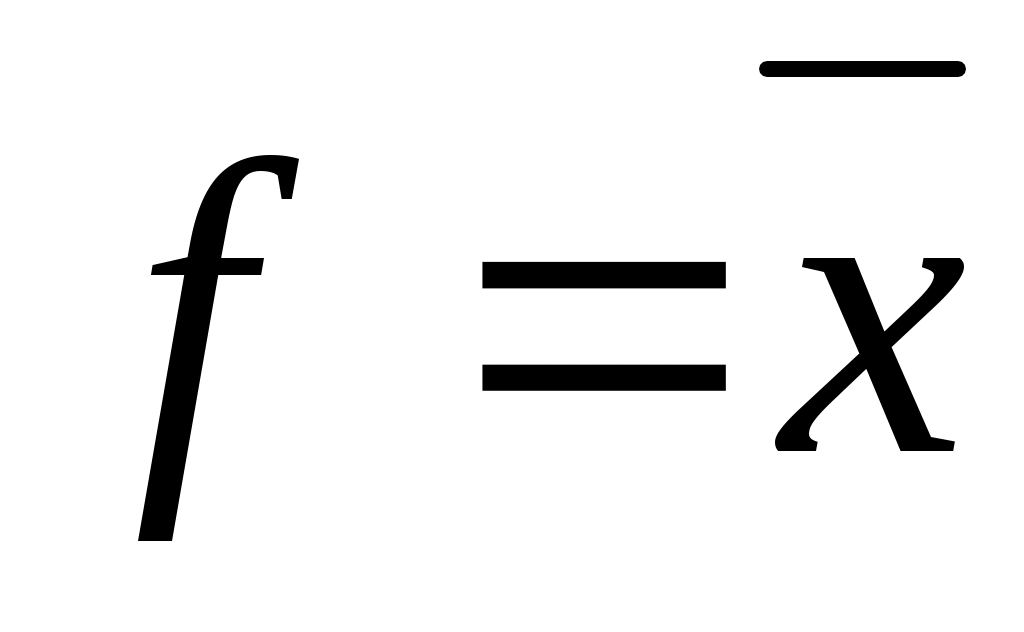
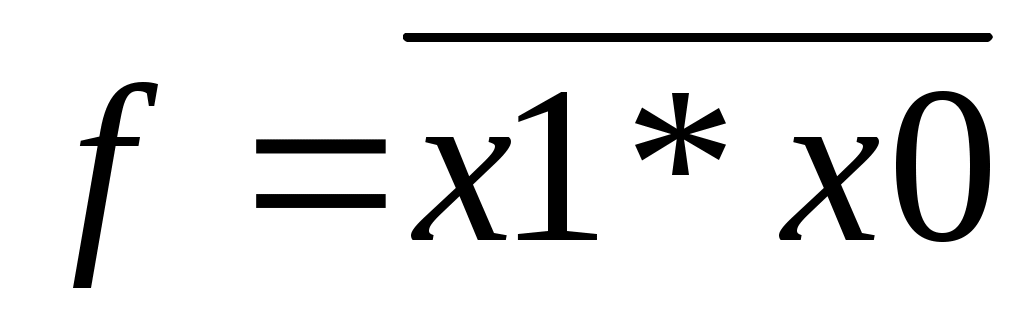

Рис2
Таблица истинности:
-
i
1
2
3
4
x1
0
1
0
1
x0
0
0
1
1
Y
f1
f2
f3
f4
1
1
0
0
Таблица 1
2. Логическая функция «ИЛИ»
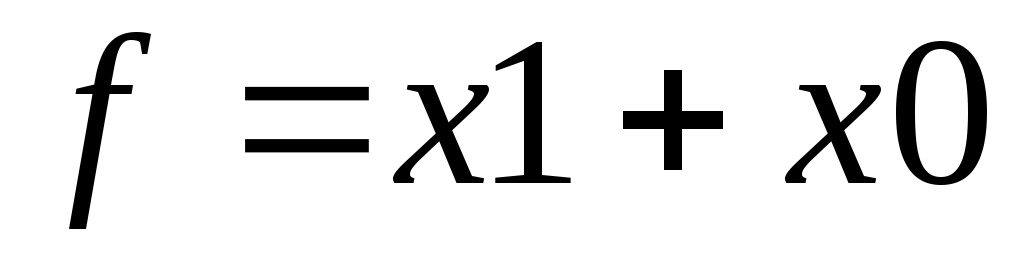
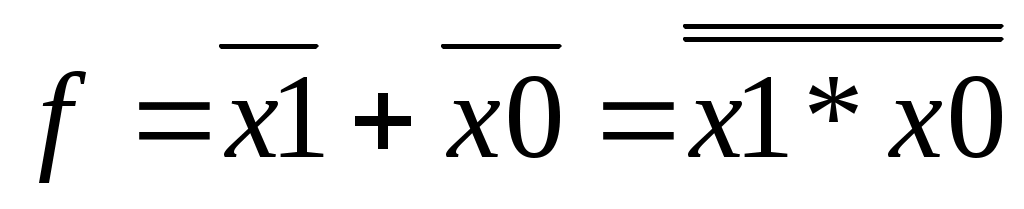

Рис 3.
Таблица истинности:
Федеральное агентство связи
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
Лабораторная работа №1
По дисциплине: Вычислительная техника и информационные технологии
Выполнил:
Группа:
Вариант: 1
Проверил: Чухров А.С.
Исследование логических схем на элементах «И–НЕ»
Цель работы:
Изучение свойств логических элементов «И–НЕ»; приобретение навыков синтеза логических схем.
Задание к лабораторной работе:
Экспериментально исследовать правила построения различных логических функций в базисе И-НЕ, снять таблицы истинности для указанных выше логических функций.
Ход работы:
1. Логическая функция «НЕ»
Схема лабораторной установки для реализации логической функции «НЕ» представлена на рисунке1.,сигнал подается на входы 2,3:
На входе 1 уровень «0»,на входе 4-«1»:

Рис 1
Логическая функция «НЕ»
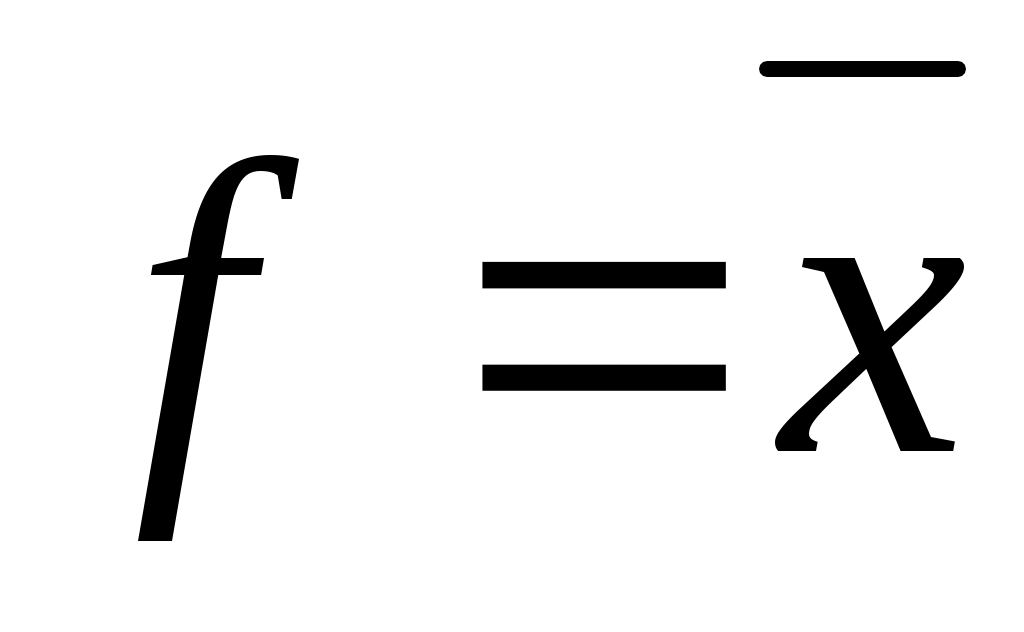
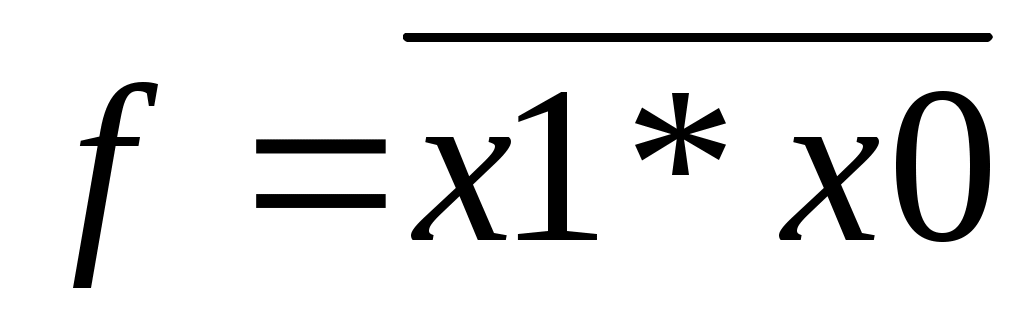

Рис2
Таблица истинности:
-
i
1
2
3
4
x1
0
1
0
1
x0
0
0
1
1
Y
f1
f2
f3
f4
1
1
0
0
Таблица 1
2. Логическая функция «ИЛИ»
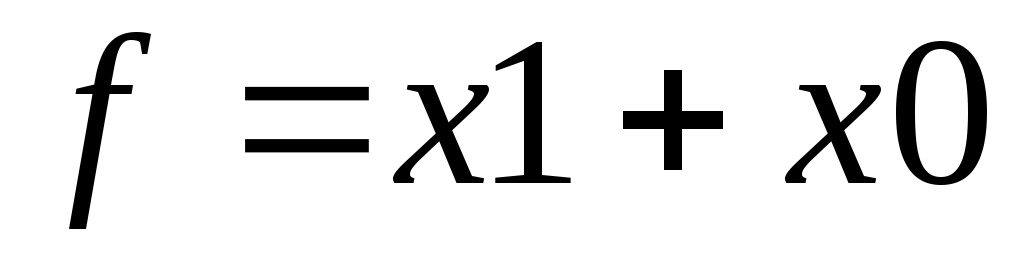
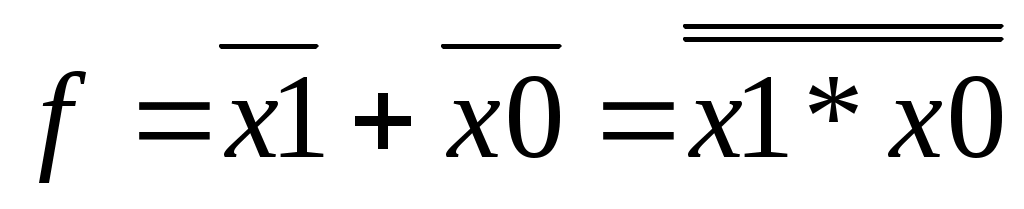

Рис 3.
Таблица истинности:
Федеральное агентство связи
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
Лабораторная работа №1
По дисциплине: Вычислительная техника и информационные технологии
Выполнил:
Группа:
Вариант: 1
Проверил: Чухров А.С.
Исследование логических схем на элементах «И–НЕ»
Цель работы:
Изучение свойств логических элементов «И–НЕ»; приобретение навыков синтеза логических схем.
Задание к лабораторной работе:
Экспериментально исследовать правила построения различных логических функций в базисе И-НЕ, снять таблицы истинности для указанных выше логических функций.
Ход работы:
1. Логическая функция «НЕ»
Схема лабораторной установки для реализации логической функции «НЕ» представлена на рисунке1.,сигнал подается на входы 2,3:
На входе 1 уровень «0»,на входе 4-«1»:

Рис 1
Логическая функция «НЕ»
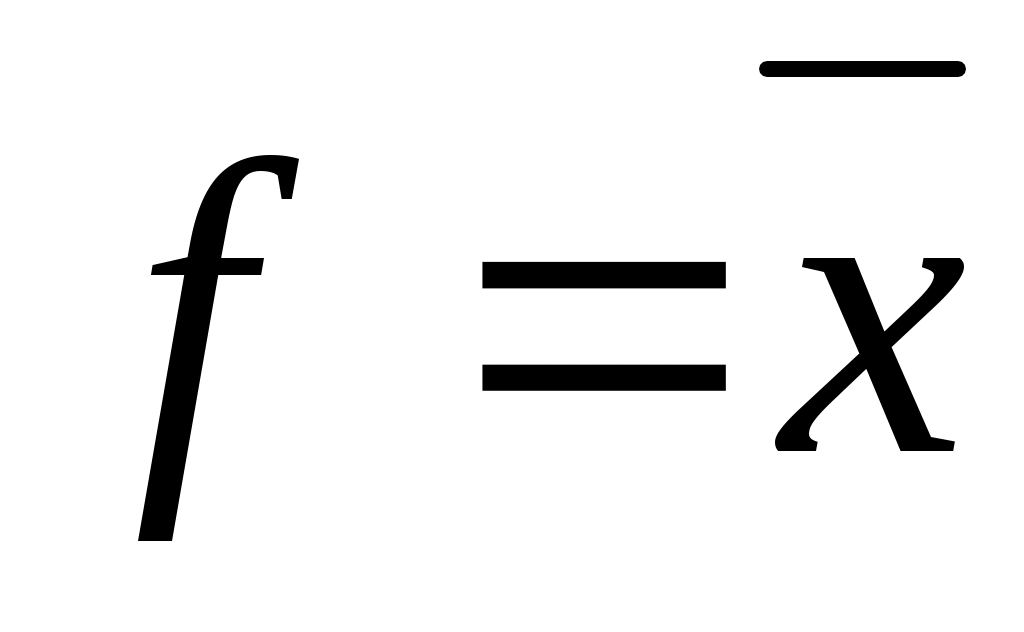
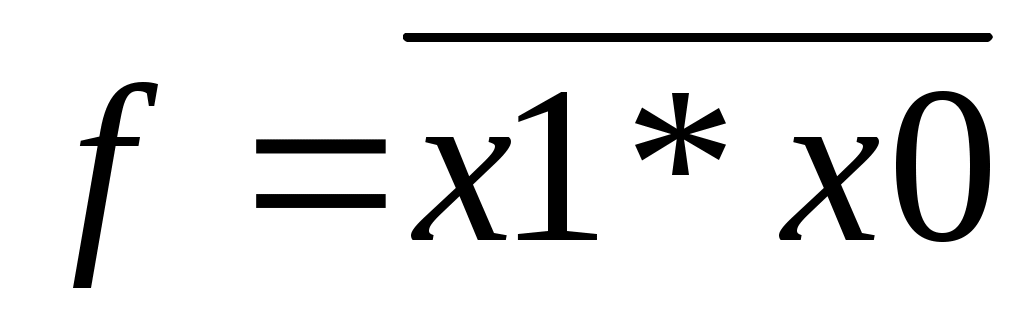

Рис2
Таблица истинности:
-
i
1
2
3
4
x1
0
1
0
1
x0
0
0
1
1
Y
f1
f2
f3
f4
1
1
0
0
Таблица 1
2. Логическая функция «ИЛИ»
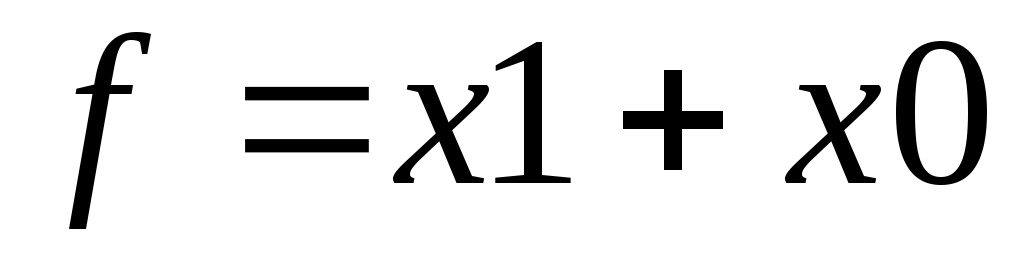
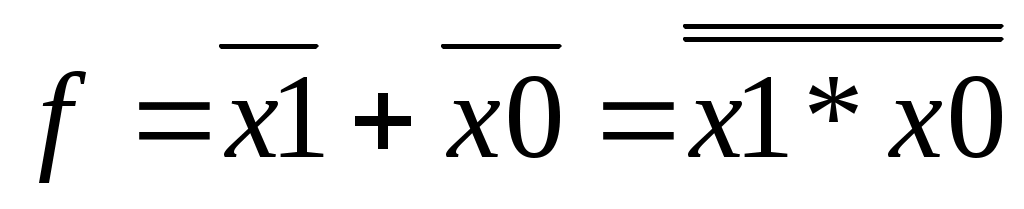

Рис 3.
Таблица истинности:
Федеральное агентство связи
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
Лабораторная работа №1
По дисциплине: Вычислительная техника и информационные технологии
Выполнил:
Группа:
Вариант: 1
Проверил: Чухров А.С.
Исследование логических схем на элементах «И–НЕ»
Цель работы:
Изучение свойств логических элементов «И–НЕ»; приобретение навыков синтеза логических схем.
Задание к лабораторной работе:
Экспериментально исследовать правила построения различных логических функций в базисе И-НЕ, снять таблицы истинности для указанных выше логических функций.
Ход работы:
1. Логическая функция «НЕ»
Схема лабораторной установки для реализации логической функции «НЕ» представлена на рисунке1.,сигнал подается на входы 2,3:
На входе 1 уровень «0»,на входе 4-«1»:

Рис 1
Логическая функция «НЕ»
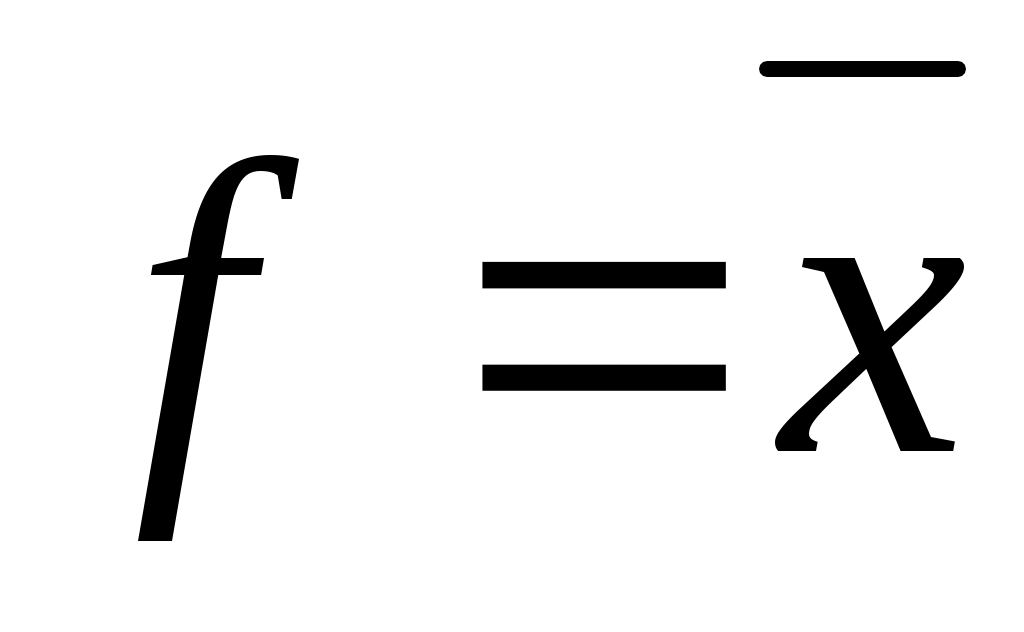
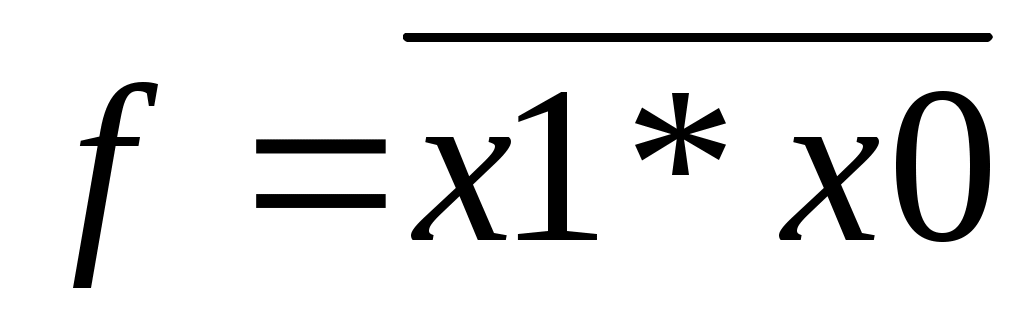

Рис2
Таблица истинности:
-
i
1
2
3
4
x1
0
1
0
1
x0
0
0
1
1
Y
f1
f2
f3
f4
1
1
0
0
Таблица 1
2. Логическая функция «ИЛИ»
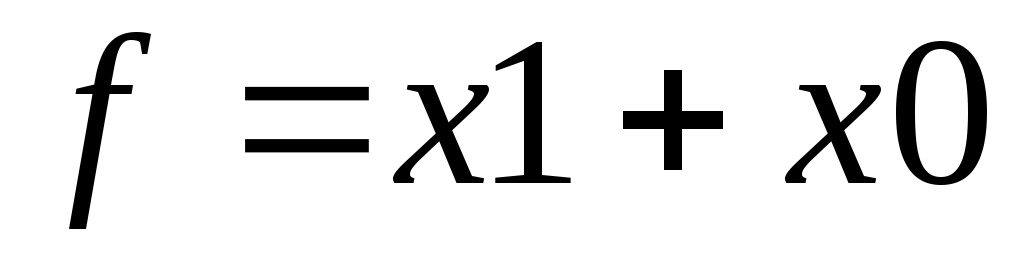
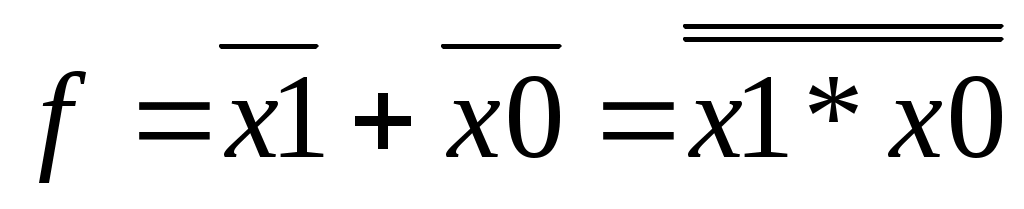

Рис 3.
Таблица истинности:
Федеральное агентство связи
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
Лабораторная работа №1
По дисциплине: Вычислительная техника и информационные технологии
Выполнил:
Группа:
Вариант: 1
Проверил: Чухров А.С.
Исследование логических схем на элементах «И–НЕ»
Цель работы:
Изучение свойств логических элементов «И–НЕ»; приобретение навыков синтеза логических схем.
Задание к лабораторной работе:
Экспериментально исследовать правила построения различных логических функций в базисе И-НЕ, снять таблицы истинности для указанных выше логических функций.
Ход работы:
1. Логическая функция «НЕ»
Схема лабораторной установки для реализации логической функции «НЕ» представлена на рисунке1.,сигнал подается на входы 2,3:
На входе 1 уровень «0»,на входе 4-«1»:

Рис 1
Логическая функция «НЕ»
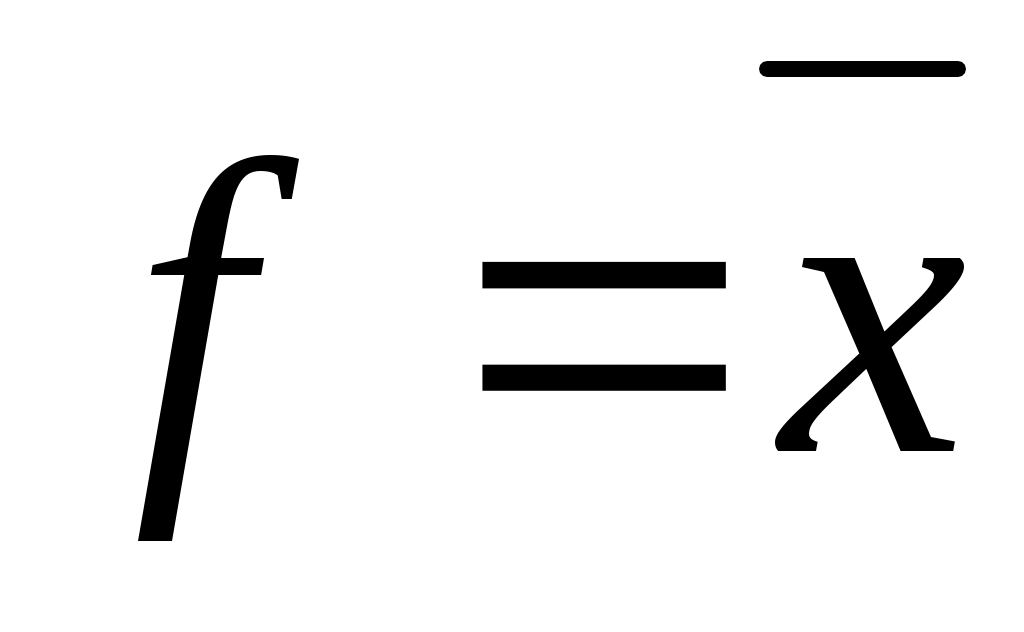
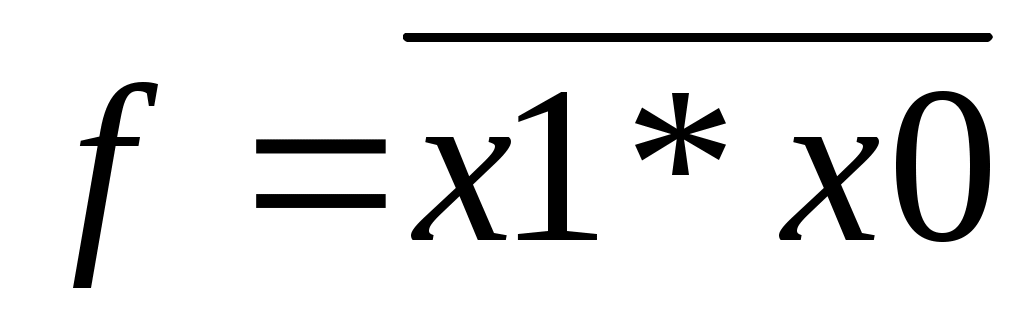

Рис2
Таблица истинности:
-
i
1
2
3
4
x1
0
1
0
1
x0
0
0
1
1
Y
f1
f2
f3
f4
1
1
0
0
Таблица 1
2. Логическая функция «ИЛИ»
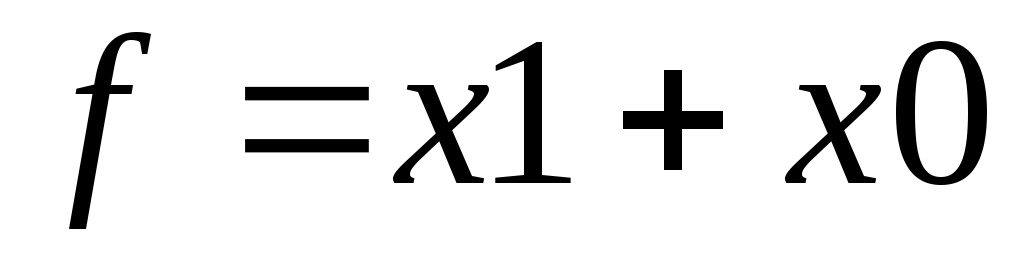
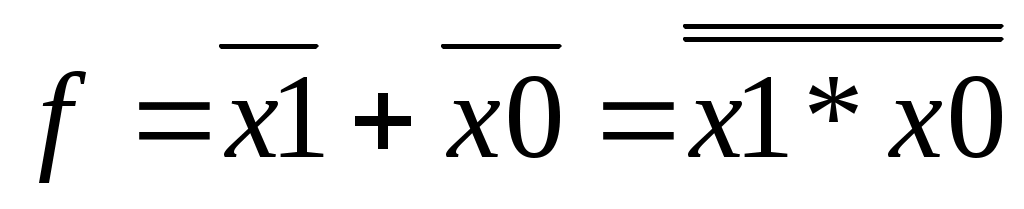

Рис 3.
Таблица истинности:
Федеральное агентство связи
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
Лабораторная работа №1
По дисциплине: Вычислительная техника и информационные технологии
Выполнил:
Группа:
Вариант: 1
Проверил: Чухров А.С.
Исследование логических схем на элементах «И–НЕ»
Цель работы:
Изучение свойств логических элементов «И–НЕ»; приобретение навыков синтеза логических схем.
Задание к лабораторной работе:
Экспериментально исследовать правила построения различных логических функций в базисе И-НЕ, снять таблицы истинности для указанных выше логических функций.
Ход работы:
1. Логическая функция «НЕ»
Схема лабораторной установки для реализации логической функции «НЕ» представлена на рисунке1.,сигнал подается на входы 2,3:
На входе 1 уровень «0»,на входе 4-«1»:

Рис 1
Логическая функция «НЕ»
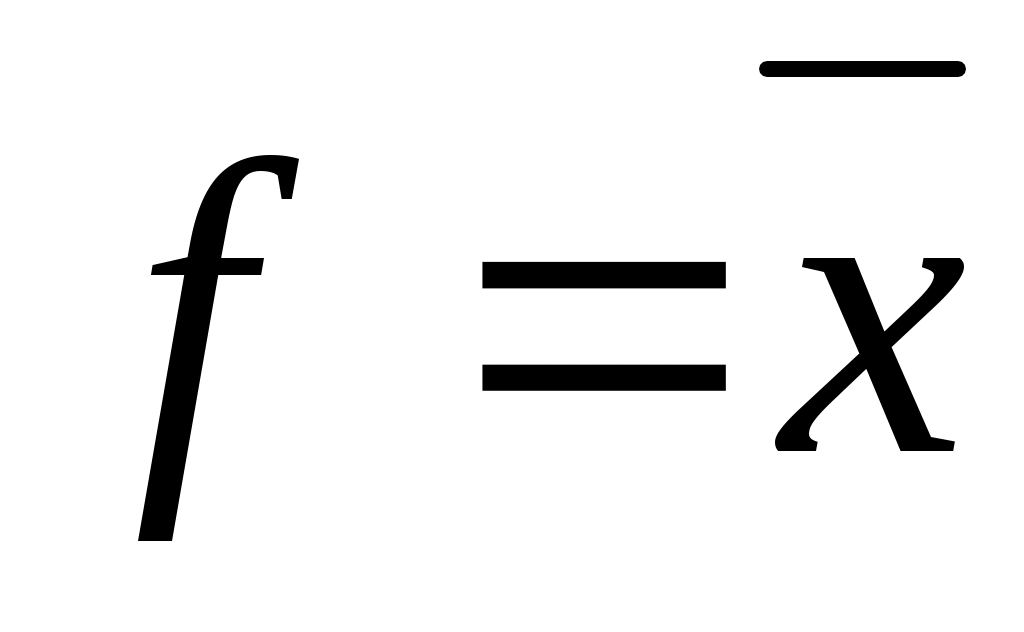
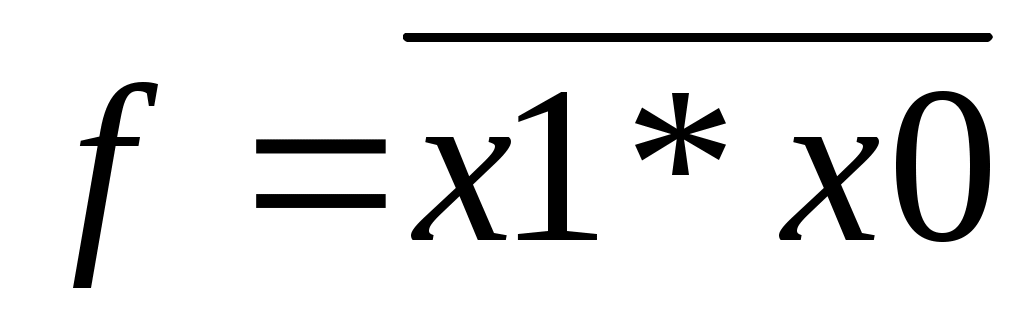

Рис2
Таблица истинности:
-
i
1
2
3
4
x1
0
1
0
1
x0
0
0
1
1
Y
f1
f2
f3
f4
1
1
0
0
Таблица 1
2. Логическая функция «ИЛИ»
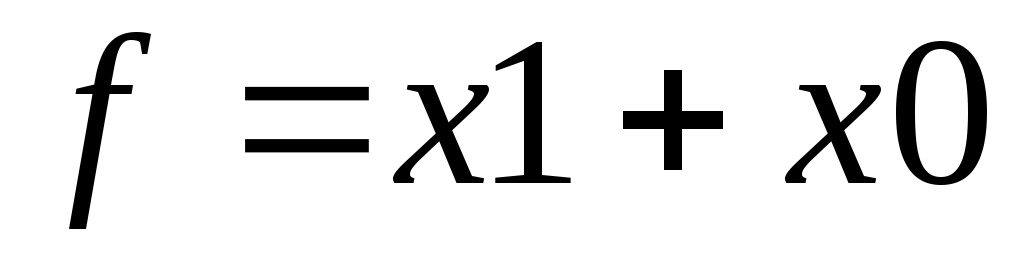
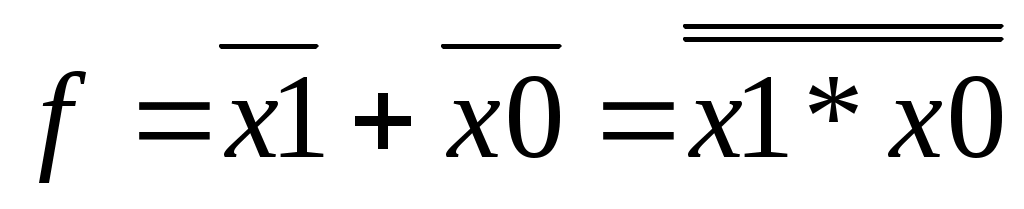

Рис 3.
Таблица истинности:
-
i
1
2
3
4
x1
0
1
0
1
x0
0
0
1
1
Y
f1
f2
f3
f4
1
1
0
0
| i | 1 | 2 | 3 | 4 |
| x1 | 0 | 1 | 0 | 1 |
| x0 | 0 | 0 | 1 | 1 |
| Y | f1 | f2 | f3 | f4 |
| 0 | 1 | 1 | 1 |
Таблица 2.
Для реализации логической функции «ИЛИ» исключаем последний элемент Схема представлена на рисунке 4.,сигнал подается на входы 2,3:
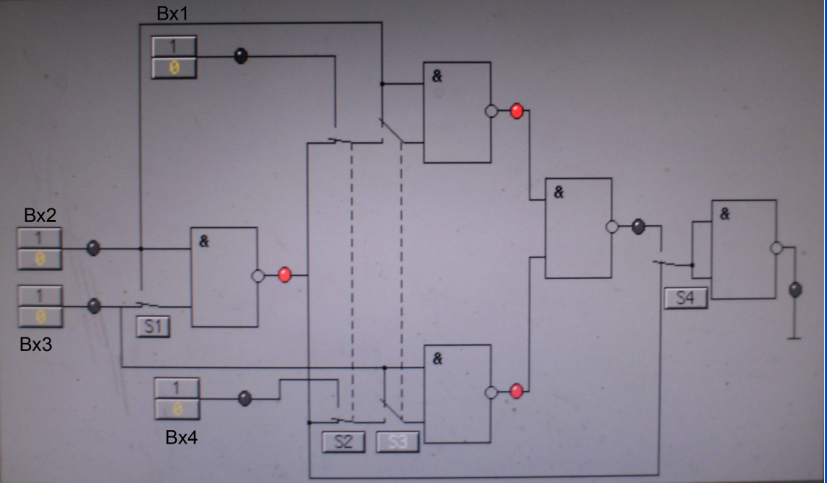
Рис 4.
3. Логическая функция «Исключающее ИЛИ»
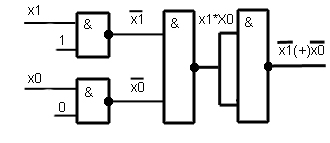
Рис 5.
Таблица истинности:
-
i
1
2
3
4
x1
0
1
0
1
x0
0
0
1
1
Y
f1
f2
f3
f4
0
1
1
0
Таблица 3
Схема лабораторной установки для реализации логической функции «Исключающее ИЛИ» представлена на рисунке 6.
Сигнал подается на входы 2,4:
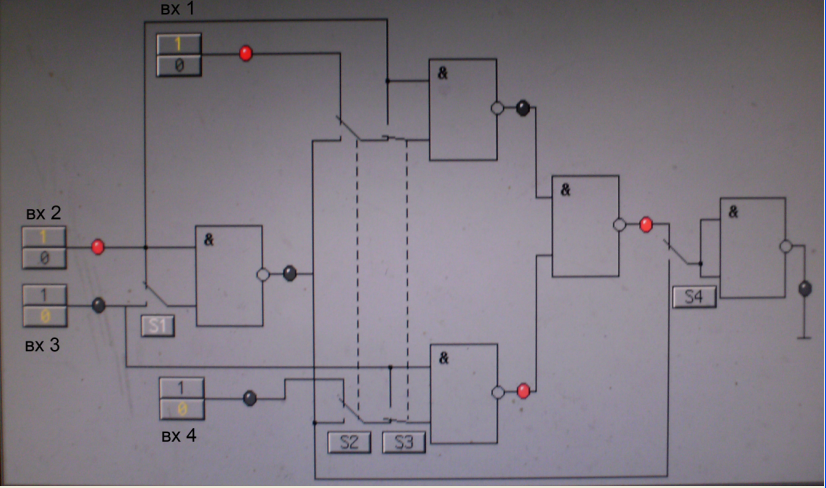
Рис 6.
4. Логическая функция «ИЛИ-НЕ»
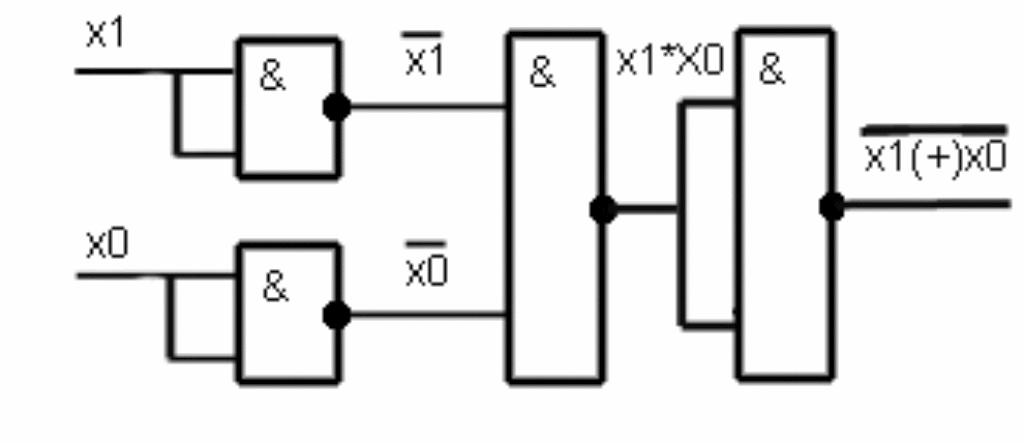
Рис 9.
Таблица истинности:
-
i
1
2
3
4
x1
0
1
0
1
x0
0
0
1
1
Y
f1
f2
f3
f4
1
0
0
0
Таблица 4.
Схема лабораторной установки для реализации логической функции «ИЛИ-НЕ» представлена на рисунке 10. Сигнал подается на входы 2,3:
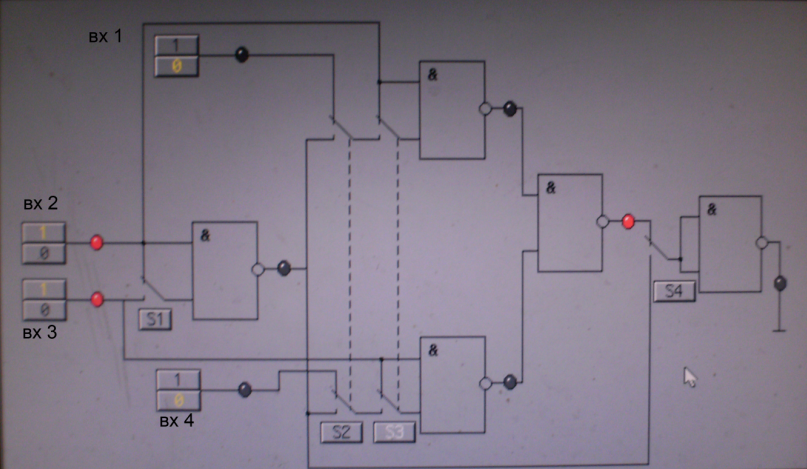
Рис 10.
5. Логическая функция «И-НЕ»
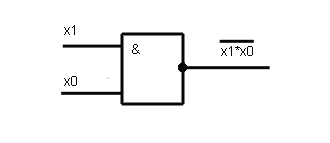
Рис 11.
Таблица истинности:
-
i
1
2
3
4
x1
0
1
0
1
x0
0
0
1
1
Y
f1
f2
f3
f4
1
1
1
0
Таблица 5.
Схема лабораторной установки для реализации логической функции «И-НЕ» представлена на рисунке 12,сигнал подается на входы 1,3:
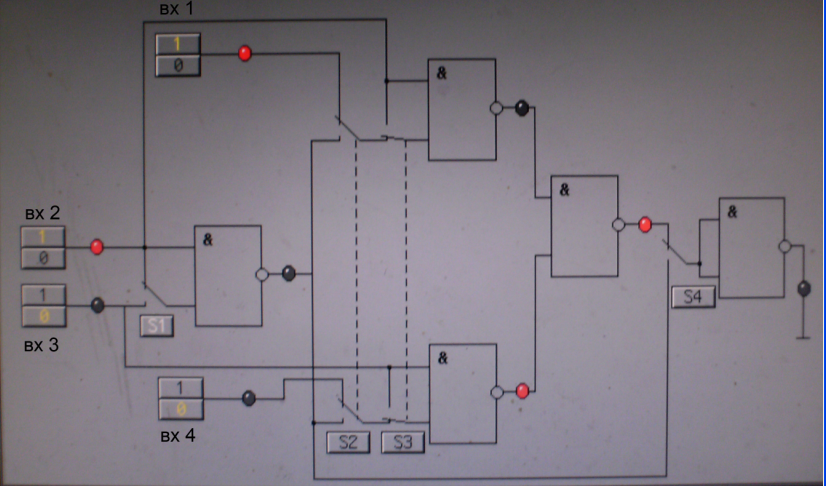
Рис 12.
6. Логическая функция «Исключающее ИЛИ-НЕ»
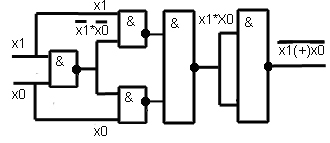
Рис13
Таблица истинности:
-
i
1
2
3
4
x1
0
1
0
1
x0
0
0
1
1
Y
f1
f2
f3
f4
1
0
0
1
Таблица 7
Схема лабораторной установки для реализации логической функции «Исключающее ИЛИ-НЕ» представлена на рисунке 14,сигнал подается на входы 2,3:
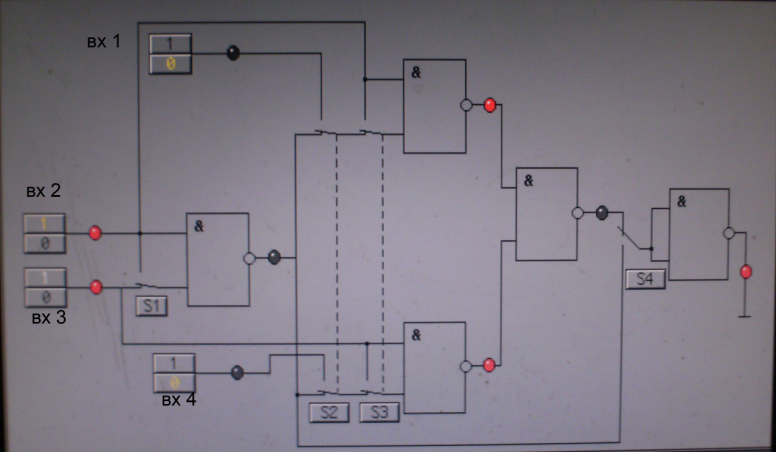
Рис 14.
7.Логическая функция «И»
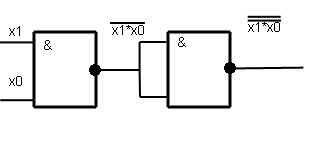
Рисунок 15.
Таблица истинности:
-
i
1
2
3
4
x1
0
1
0
1
x0
0
0
1
1
Y
f1
f2
f3
f4
0
0
0
1
Таблица 8
Схема лабораторной установки для реализации логической функции «И» представлена на рисунке16,сигнал подается на входы 1,2:
Рис 16.
Контрольные вопросы:
-
Что такое полный и минимальный базис?
Набор простейших логических функций, позволяющих реализовать любую другую функцию называется логическим базисом (ЛБ). Функции И, ИЛИ, НЕ не являются минимальным ЛБ, т.к. сами могут быть представлены через другие функции, например через F14(И - НЕ).
«НЕ»: x=(x*1)=(x*x)
«ИЛИ» : х1+х2 = (х1*х2)
«И»: х1*х2 = ((х1*х2)
Следовательно базис "И - НЕ" является минимальным.
-
Почему логический элемент И – НЕ обладает функциональной полнотой?
Функционально полная система логических функций представляет собой набор логических функций, с помощью которых можно записать любую, сколь угодно сложную функцию. В этом случае говорят, что этот набор образует базис. Функционально полными являются 3 базиса:
"И-ИЛИ-НЕ" (базис конъюнкции, дизъюнкции, инверсии)
"И-НЕ" (базис Шеффера)
"ИЛИ-НЕ" (базис Пирса или функция Вебба).
-
Основные свойства логических функций.
0 + 0 = 0 (1) 1 * 1 = 1 (1')
1 + 1 = 1 (2) 0 * 0 = 0 (2')
1 + 0 = 0 + 1 = 1 (3) 0 * 1 = 1 * 0 = 0 (3')
1 = 0 (4) 0 = 1 (4')
Из (1, 2) и (1',2') следует: x + x = x и x * x = x. (5)
Из (1, 3) и (2',3') следует: x + 0 = x и 0 * x = 0. (6)
Из (2, 3) и (1',3') следует: 1 + x = 1 и x * 1 = x. (7)
Из (3) и (3') следует: x +x = 1 иx * x = 0. (8)
Из (4) и (4') следует: (x) = x. (9)
-
Дайте формулировку правила де Моргана.
Теорема Де Моргана (инверсия логической суммы равна логическому произведению инверсий и наоборот) :
( x0+x1 ) = x0 * x1 и ( x0 * x1) = x0 + x1
-
Какова цель минимизации логических функций?
Минимизация логической функции - это процесс представления ее в виде минимального количества элементарных функций.
