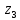Файл: Самостоятельная работа По дисциплине Проектирование гражданских зданий.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.03.2024
Просмотров: 21
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное образовательное учреждение высшего образования
«Саратовский государственный технический университет имени Гагарина Ю.А.»
Кафедра: «Строительные материалы, конструкции и технологии» (СМКТ)
Самостоятельная работа
По дисциплине «Проектирование гражданских зданий»
Вариант № 1
Выполнил студент группы:
Б-СТЗСз-31
Астарханов Р.А.
Шифр: 202163
Проверил: ст. преп.каф. СМКТ:
Пименов Д.А.
Саратов 2023
Содержание
Лист задания 3
Задание 1 3
Задание 2 6
Задание 3 13
Задание 4 19
Задание 5 25
Задание 6 25
Заключение 26
Список литературы 27
| № сечения | Размер 1 мм | Размер 2 мм | Размер 3 мм | А1 мм | |||
| 1 | 50 | 100 | 50 | 100 | 50 | 100 | 25 |
Задание №1
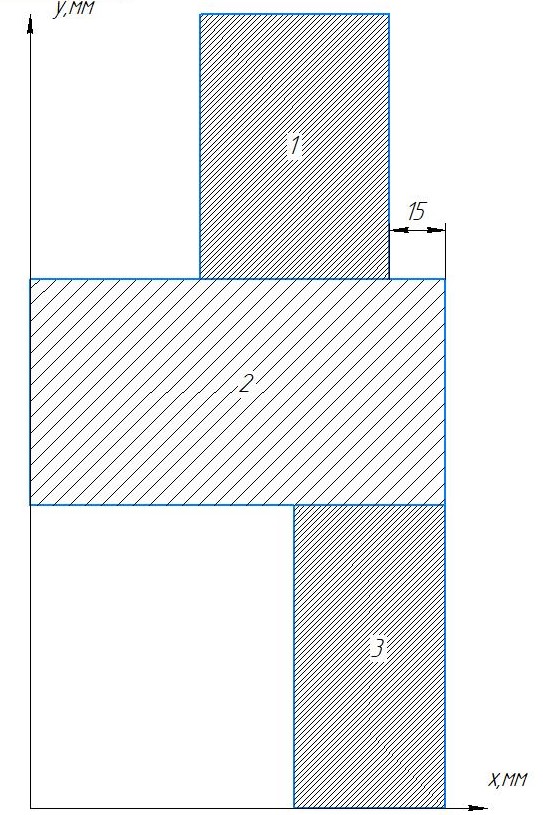
Рис.1- Поперечное сечение конструкции
Решение
1)Для определения статистического момента площади поперечного сечения конструкции (ПСК) расположим оси х и у согласно рис.1
Для интегрального выражения координат центра тяжести воспользуемся формулой:
Ус=
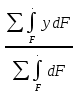(1)где выражение в числителе дроби значит интегральная сумма от произведения бесконечно малой площадки dF на расстояние от её центра тяжести до оси х.
А в знаменателе интегральная сумма от площади ПСК из множества бесконечно малых площадок dF
Аналогичное выражение для х
с
хс=
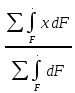(2)Так как большинство известных строительных сечений состоят из простых сечений, то формулы (1) и (2) можно выразить так:
ус=
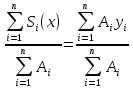(3)xс=
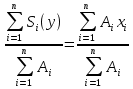(4)Итого, статический момент площади ПСК для выбранного вариант будет вычислен следующим образом:
ус=
=
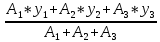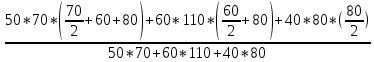=110ммхс=
=
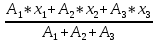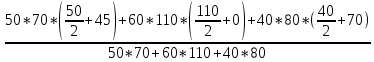=67ммКоординаты центра тяжести ПСК:
хс=67 мм ус=110 мм
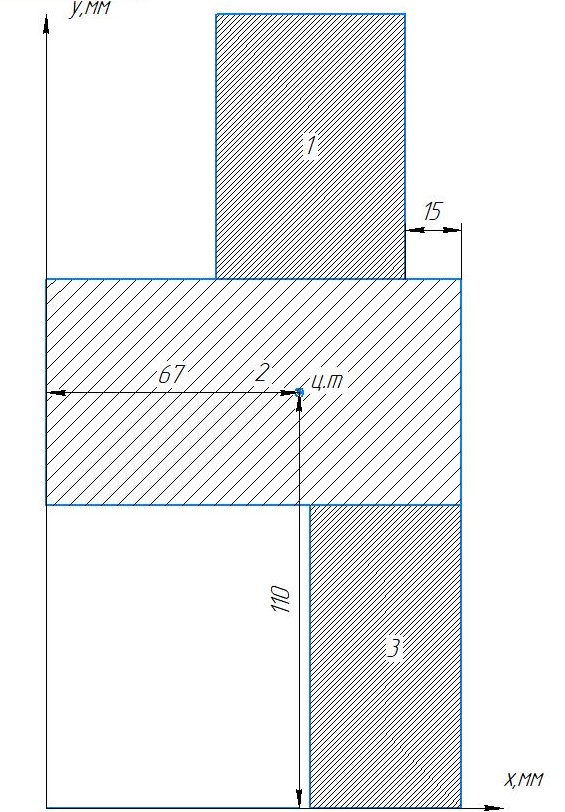
Рис 2- центр тяжести сложного поперечного сечения конструкции
2)Осевой момент инерции ПСК относительно его центра тяжести для осей у и х выразим в интегральном виде, как:
Jx=
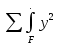dF ; Jy=
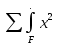dFТакже интегрально выразим центробежный момент инерции ПСК:
Jyх=
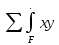dF;Так как для центры тяжести размеров 1-3 не совпадают с центром тяжести ПСК, то при вычислении Jx, Jy, Jyх учтём добавление соответственно:
;
; 
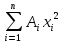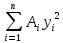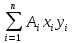
Следовательно, значение этих характеристик ПСК, используя известную формулу для прямоугольников вида
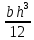, находим, как:Jy=
+
+
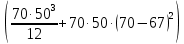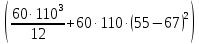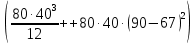=10 485 533 мм^4Jx
+
+
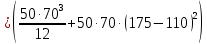
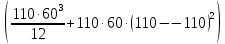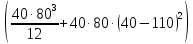=35 583 333 мм^4Jyх=
+
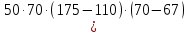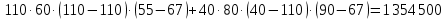мм^4Итого в см^4
Jx
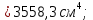Jy=1048,6 см^4 ; Jyх=1354,5 .3) Момент сопротивления изгибу ПСК находим для верхнего и нижнего крайних волокон, как:
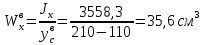
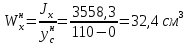
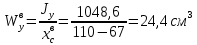
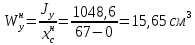
Задание №2
Конструктивный элемент
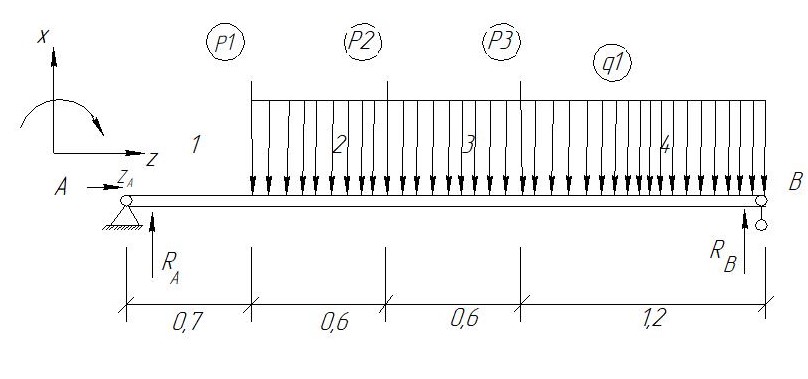
Рис 3-Конструктивный элемент
Дано:
Р1=100 кг
Р2=110 кг
Р3=50 кг
q1=25 кг/м
Решение:
1) ОХ:
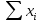=0 ;ОZ:
=0 ;MA:
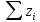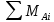=0 ;Выше приведены условия равенства нагрузок и опорных реакций нулю составляют три уравнения статики. Решением этой системы уравнений и будут искомые опорные реакции.
Выразим эти условия для данного варианта:
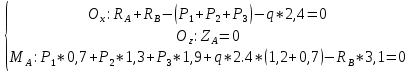
Из
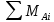=0 получаем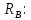 
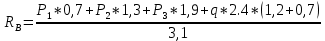=242,03 кгсПодставляя в
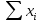=0, получим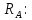 
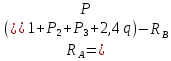=287,2кгсИтого
=
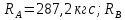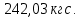
2)Для определения поперечных сил в балке разделим её на 4 сектора
Сектор 1-1
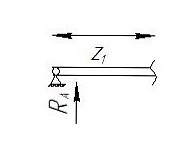
Рис 4-Исследуемый участок №1
Q(
)=
Сектор 2-2
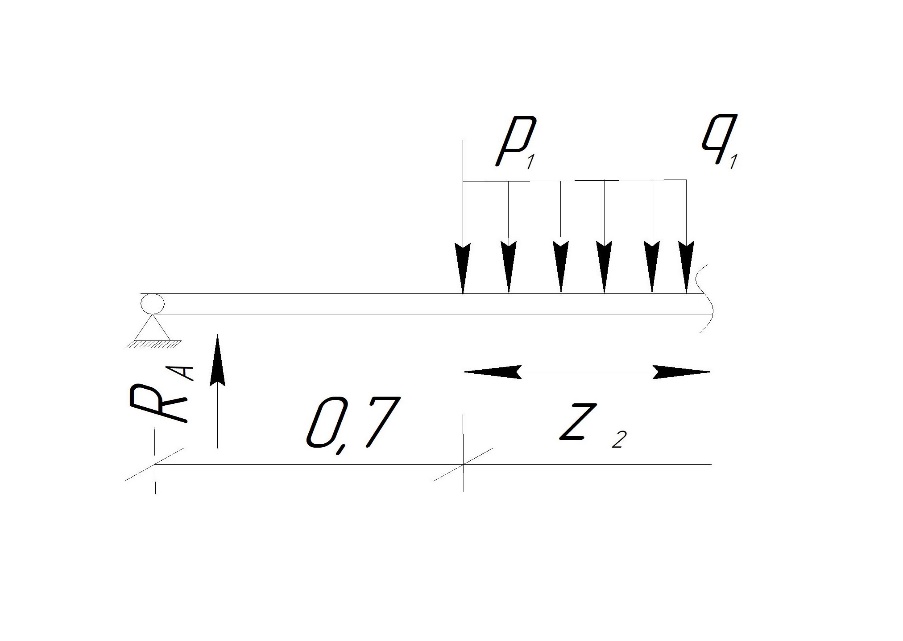
Рис 5-Исследуемый участок №2
Q(
)=
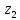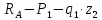
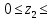0,6мQ(
)=
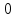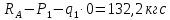
Q(
)=
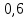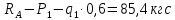
Сектор 3-3
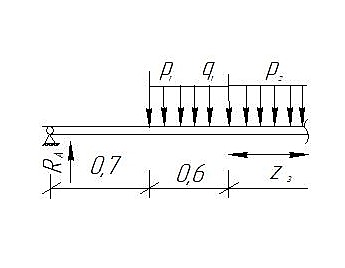
Рис 6-Исследуемый участок № 3
Q(
)=
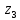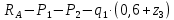
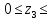0,6мQ(
)=
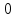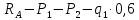=-6,6 кгсQ(
)=
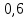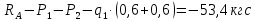
Сектор 4-4
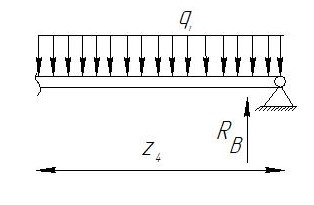
Рис 5-Исследуемый участок №4
Q(
)=
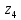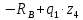
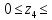1,2мQ(
)=
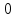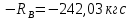
Q(
)=
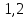По полученным значениям поперечных сил в характерных точках балки построим эпюру этих сил:
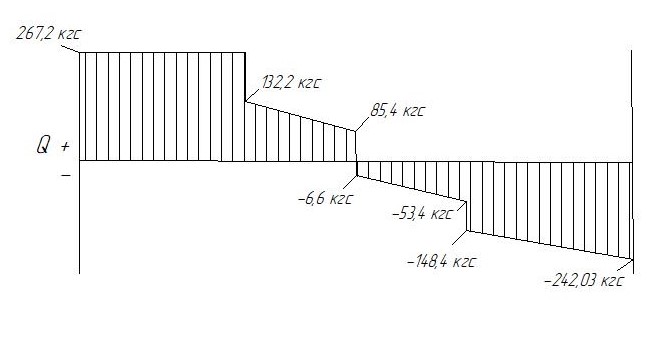
Рис 6- Эпюра поперечных сил
3) По тому же методу определим значение изгибающих моментов, возникающих в точках балки:
Сектор 1-1
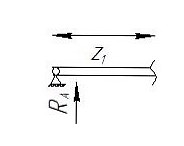
M(
)=
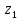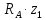
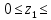0,7мM(
)=
0 кгс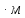
M(
)=
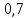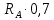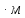
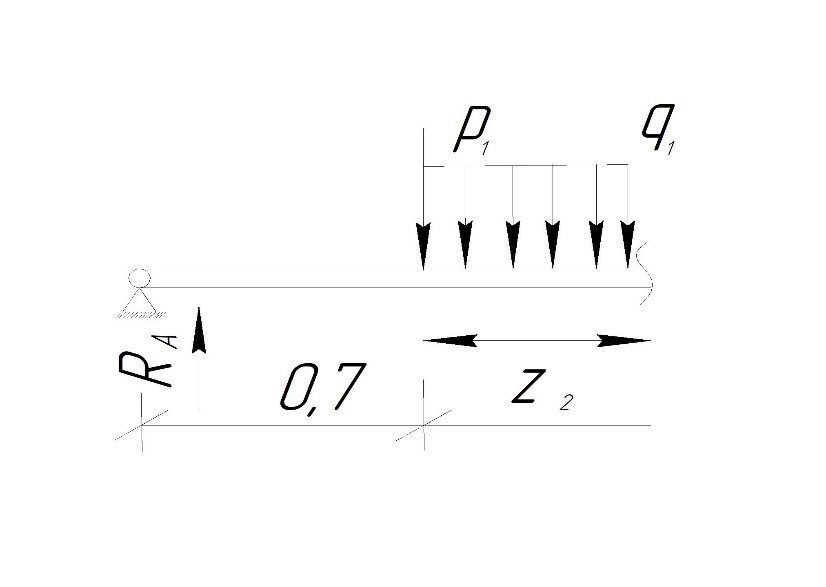
=187,0 кгс Сектор 2-2
M(
)=
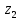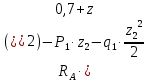
0,6мM(
)=
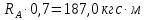
M(
)=
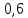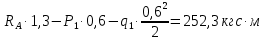
Так как на секторе 2-2 эпюра поперечных сил не является двухзначной , экстремумов функции M(
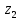) на этом секторе нет.Сектор 3-3
M(
)=
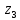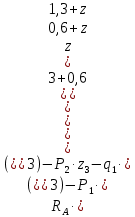
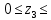0,6мM(
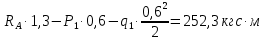
)= M(
)=
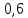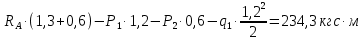
На этом секторе нет экстремумов функции M(