Файл: Самостоятельная работа По дисциплине Проектирование гражданских зданий.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.03.2024
Просмотров: 22
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
), т.к. функция Q(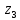
) не двузначна. Переход от +Q к –Q происходит в пределе границ секторов 2-2 и 3-3,поэтому максимальное значение изгибающего момента будет в этой точке.
Сектор 4-4
M(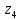
)=
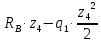
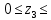1,2м
M(
)=
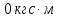
M(
)=
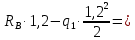234,2 кгс
По вычисленным значениям изгибающего момента в балке построим эпюру:
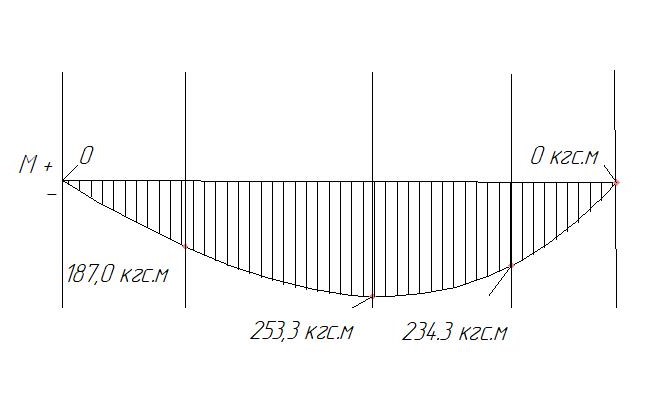
Задание 3
Дано
Условие допустимого напряжения в конструктивном элементе выражается, как:
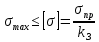
где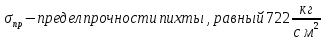
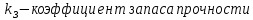
Максимальное значение напряжения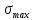
будет определено в зависимости от максимального изгибающего момента , возникающего в балке с учётом всех коэффициентов надёжности для нагрузок.
Для этого определим расчётное значение нагрузок:
Сосредоточенные:
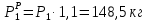
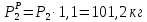
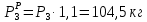
Распределённая:
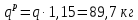
Собственный вес:
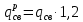
Нормативное значение собственного веса балки определим , как :
=
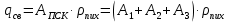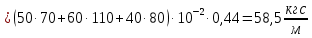
Итак, расчётное значение ,равно:
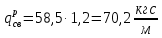
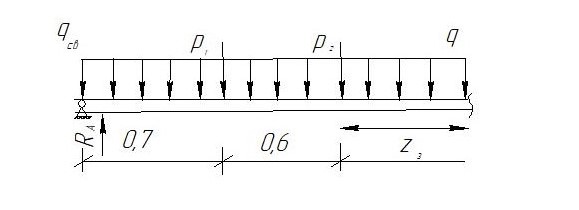
Определим опорные реакции расчётной схемы для нашего варианта по последовательности аналогичной, как в задании №2
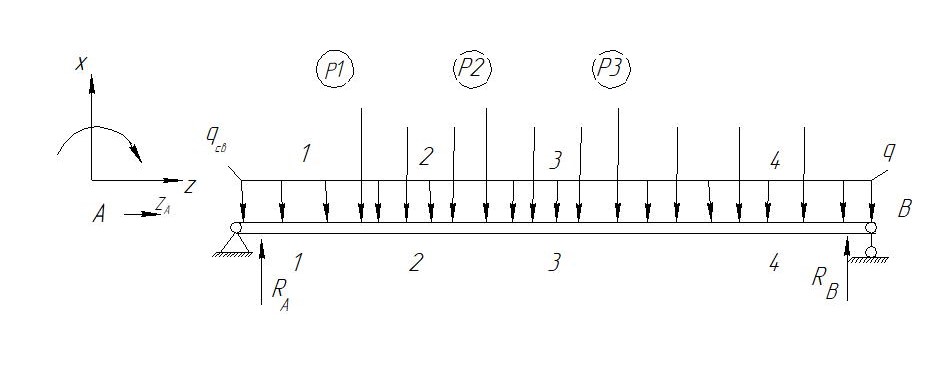
Условие геометрической неизменяемости:
∑
; ∑
; ∑
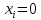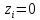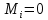
Находим исходные опорные реакции:
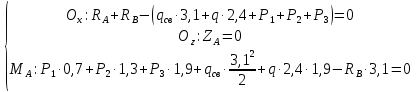
Из
=0 получаем 
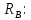
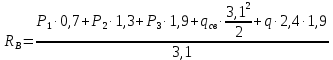=380,4 кгс
=
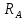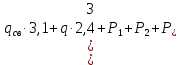=405,6 кгс
Величины поперечных сил изгибающих моментов по секторам будут выражены, так:
Сектор 1-1
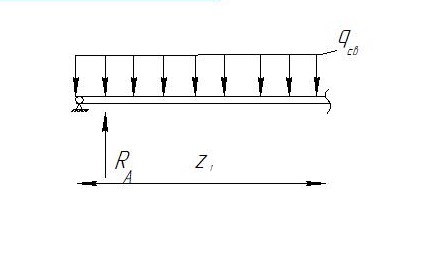
Q(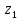
)=
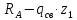
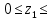0,7м
Q( )=
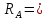405,6кгс
Q(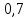
)=
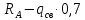=356,6 кгс
M( )=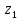
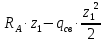
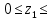0,7м
M( )=
0 кгс
M( )=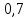
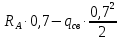=266,8 кгс
Сектор 2-2
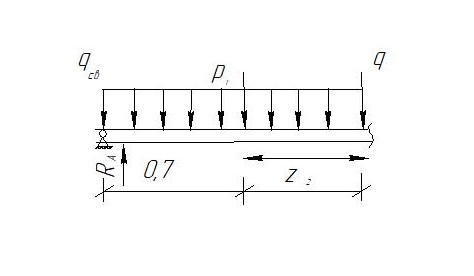
Q(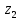
)=
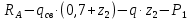
0,6м
Q( )=
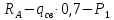=208,6 кгс
Q(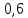
)=
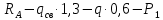=112,6 кгс
M( )=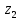
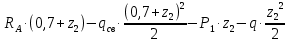
0,6м
M( )=
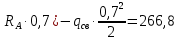кгс
M( )=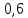
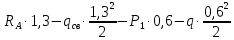=363,2 кгс
Сектор 3-3
Q( )=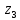
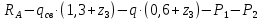
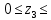0,6 м
Q( )=
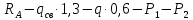=11,6 кгс
Q( )=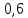
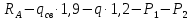=-84,4 кгс
M( )=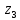
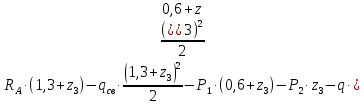
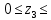0,6м
M( )=
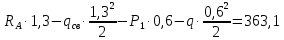кгс
M( )=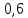
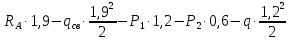=341,2 кгс
Сектор 4-4
Q( )=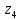
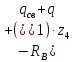
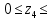1,2м
Q( )=
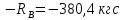
Q( )=
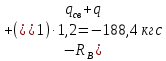
M( )=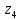
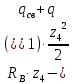
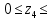1,2м
M( )=
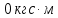
M( )=
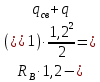341,3 кгс
По вычисленным значениям внутренних усилий построим эпюры: поперечных сил Q и изгибающих моментов М
1.Эпюра поперечных сил
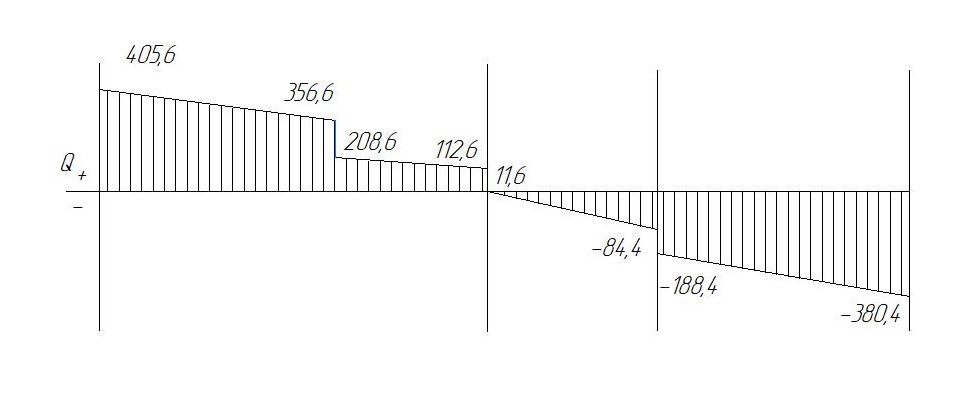2.Эпюра изгибающих моментов
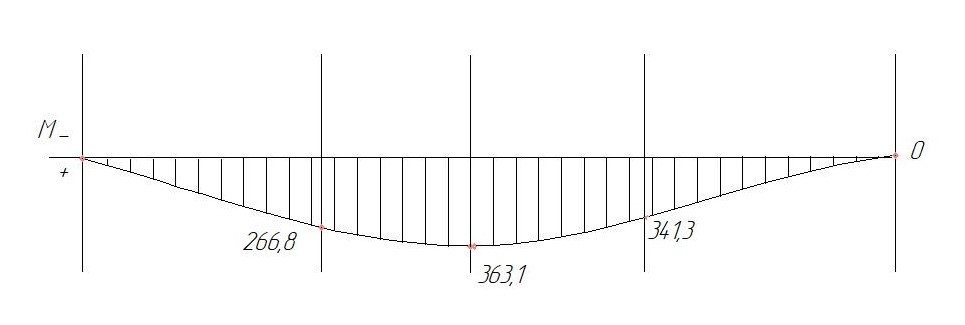
Так как переход +Q к Q переходит фактически в характерной точке под приложением P2.
Значит, максимальное значение изгибающего момента, будет в этой точке:
Ммах=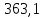
кгс
Максимальное напряжение для верхних волокон ПСК выражается, как:
=
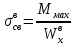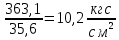
Аналогично для нижних волокон
=
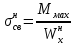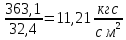
Примем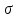
мах=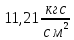
В соответствии с выше приведённом условием:
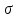мах=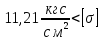
=
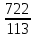=555,4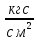
Делаю вывод, что прочность конструктивного элемента при заданном ПСК обеспечена с большим запасом.
Задание №4
Также вычислим условия перемещения и прогибы балки от заданных нормативных нагрузок с учётом добавленного собственного веса балки.
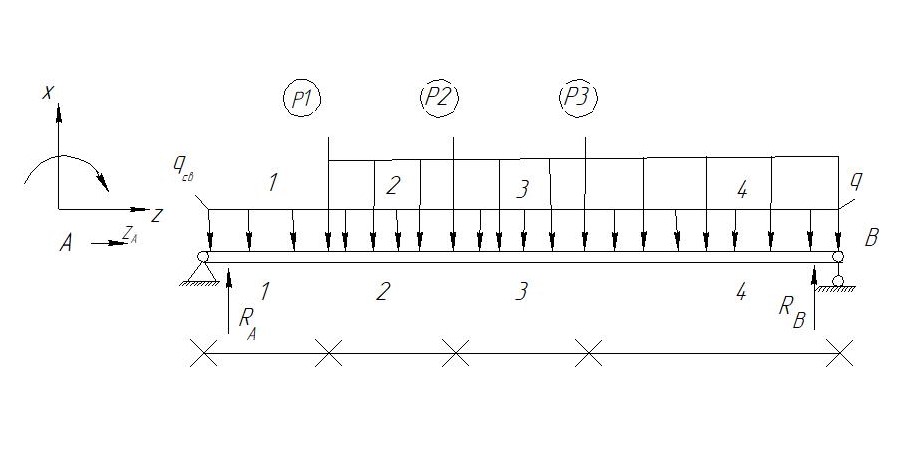
Условие геометрической неизменяемости:
∑
; ∑
; ∑
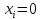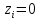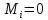
Искомые опорные реакции будут выражены, как :
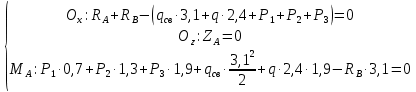
Из =0 получаем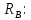
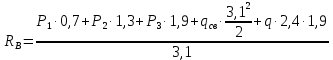=331,9 кгс
=
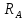=357,1 кгс
Запишем для каждого сектора уравнение поперечных сил, изгибающих моментов, угловых перемещений и прогибов:
Сектор 1-1
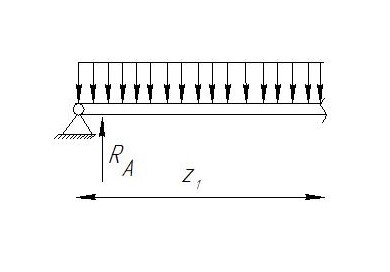
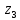) не двузначна. Переход от +Q к –Q происходит в пределе границ секторов 2-2 и 3-3,поэтому максимальное значение изгибающего момента будет в этой точке.Сектор 4-4
M(
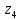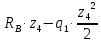
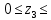)= 1,2мM(
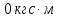
)= M(
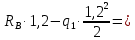)= 234,2 кгс По вычисленным значениям изгибающего момента в балке построим эпюру:
Задание 3
Дано
| Материал | Макс. перемещение | Расчетн. коэф. для P | Расчетн. коэф. для q | Расчетн. коэф. для qсв | Коэф. запаса прочности |
| Пихта | l/200 | 1.1 | 1.05 | 1.2 | 1.1 |
Условие допустимого напряжения в конструктивном элементе выражается, как:
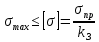
где
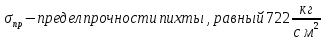
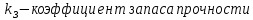
Максимальное значение напряжения
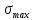будет определено в зависимости от максимального изгибающего момента , возникающего в балке с учётом всех коэффициентов надёжности для нагрузок.Для этого определим расчётное значение нагрузок:
Сосредоточенные:
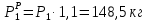
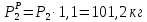
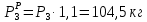
Распределённая:
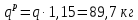
Собственный вес:
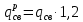
Нормативное значение собственного веса балки определим , как :
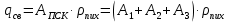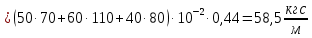
= Итак, расчётное значение ,равно:
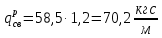
Определим опорные реакции расчётной схемы для нашего варианта по последовательности аналогичной, как в задании №2
Условие геометрической неизменяемости:
∑
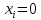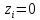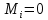
; ∑ ; ∑ Находим исходные опорные реакции:
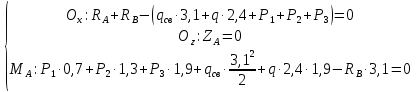
Из
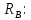
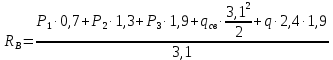=0 получаем =380,4 кгс 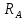= =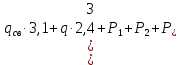405,6 кгсВеличины поперечных сил изгибающих моментов по секторам будут выражены, так:
Сектор 1-1
Q(
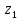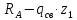
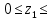)= 0,7мQ(
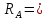)= 405,6кгсQ(
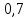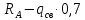)= =356,6 кгсM(
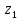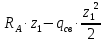
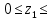)= 0,7мM(
)= 0 кгс M(
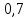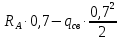)= =266,8 кгс Сектор 2-2
Q(
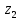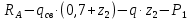
)= 0,6мQ(
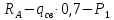)= =208,6 кгсQ(
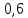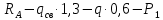)= =112,6 кгсM(
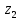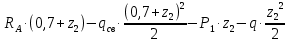
)= 0,6мM(
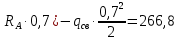)= кгс M(
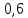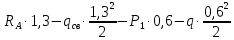)= =363,2 кгс Сектор 3-3
Q(
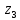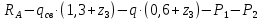
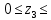)= 0,6 мQ(
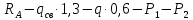)= =11,6 кгсQ(
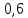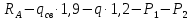)= =-84,4 кгсM(
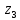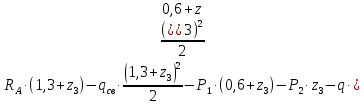
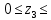)= 0,6мM(
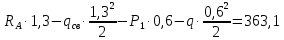)= кгс M(
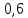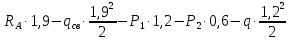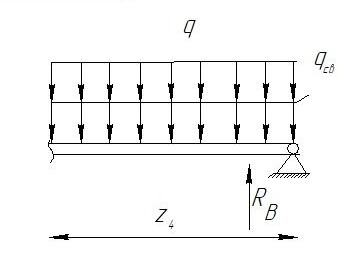
)= =341,2 кгс Сектор 4-4
Q(
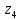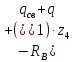
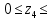)= 1,2мQ(
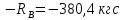
)= Q(
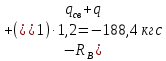
)= M(
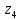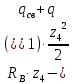
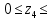)= 1,2мM(
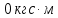
)= M(
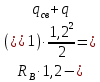)= 341,3 кгс По вычисленным значениям внутренних усилий построим эпюры: поперечных сил Q и изгибающих моментов М
1.Эпюра поперечных сил
2.Эпюра изгибающих моментов Так как переход +Q к Q переходит фактически в характерной точке под приложением P2.
Значит, максимальное значение изгибающего момента, будет в этой точке:
Ммах=
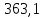
кгс
Максимальное напряжение для верхних волокон ПСК выражается, как:
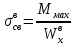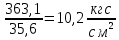
= Аналогично для нижних волокон
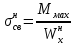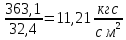
= Примем
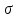мах=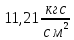 В соответствии с выше приведённом условием:
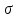мах=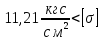 = =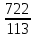555,4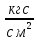 Делаю вывод, что прочность конструктивного элемента при заданном ПСК обеспечена с большим запасом.
Задание №4
Также вычислим условия перемещения и прогибы балки от заданных нормативных нагрузок с учётом добавленного собственного веса балки.
Условие геометрической неизменяемости:
∑
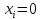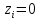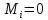
; ∑ ; ∑ Искомые опорные реакции будут выражены, как :
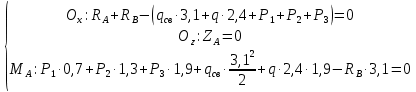
Из
=0 получаем 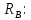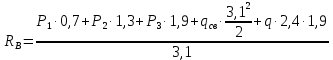=331,9 кгс 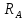= =357,1 кгсЗапишем для каждого сектора уравнение поперечных сил, изгибающих моментов, угловых перемещений и прогибов:
Сектор 1-1