Файл: Контрольная работа за 1 семестр 1 вариант Материальная точка начинает двигаться из начала координат в момент времени t 0.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.03.2024
Просмотров: 12
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное
Учреждение высшего образования
«Тульский государственный университет»
Интернет институт Тул ГУ
Тула, 2020 г.
Контрольная работа за 1 семестр
1 вариант
-
Материальная точка начинает двигаться из начала координат в момент времени t0 = 0 c нулевой начальной скоростью и ускорением, изменяющимся со временем по закону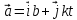 , где b = 3м/с2, k= 12м/с2. На каком расстоянии от начала координат окажется точка через время t=1c?
, где b = 3м/с2, k= 12м/с2. На каком расстоянии от начала координат окажется точка через время t=1c?
Дано:
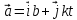
b = 3м/с2
k= 12м/с2
t
 =1c
=1cr - ?
Решение:
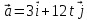
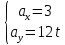
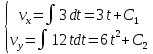
Если в начальный момент времени скорость точки была нулевой, то нулевыми были и проекции скорости на координатные оси
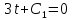
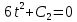
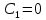
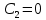 и
и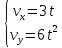
Для проекций радиус-вектора точки на координатные оси имеем
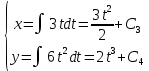
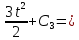 0
0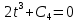
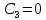
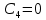 и
и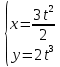
В момент времени t=1с точка будет иметь координаты
x =
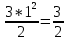
y =
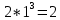
r =
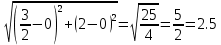
Ответ: 2,5 м
2. Сформулировать уравнения движения частицы массы m: а) в проекциях на оси x,y,z декартовой системы координат; б) в проекциях на направления касательной и нормали к траектории. Консервативна ли сила
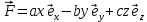 ? В случае положительного ответа найти потенциальную энергию U (x,y,z).
? В случае положительного ответа найти потенциальную энергию U (x,y,z).Для материальной точки с постоянной массой m второй закон Ньютона в векторной форме имеет вид m*
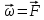 , где
, где 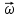 - ускорение материальной точки,
- ускорение материальной точки, 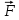 - равнодействующая сил, приложенных к ней.
- равнодействующая сил, приложенных к ней.а) В проекциях на оси декартовой прямоугольной системы координат в пространстве уравнение m*
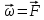 равносильно системе уравнений:
равносильно системе уравнений: 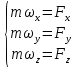
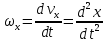 ,
, 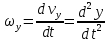 ,
, 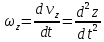
б) В проекциях на оси естественного координатного триэдра (касательная, главная нормаль, бинормаль к траектории в текущем положении материальной точки) уравнение m*
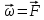 равносильно системе уравнений:
равносильно системе уравнений: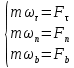
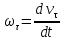 ,
, 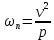 ,
, 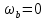 , где p – радиус кривизны траектории.
, где p – радиус кривизны траектории.
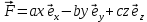
Обозначим P=ax, Q=by, R=cz. Тогда
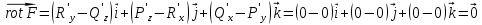
Значит, сила
 является консервативной (потенциальной).
является консервативной (потенциальной).Что бы найти потенциал U(x,y,z) :
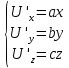
Интегрируя первое уравнение системы по x
U=
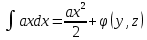
Роль постоянной интегрирования играет любая функция
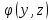 , так как её частная производная по x равна нулю. Далее дифференцируем полученную функцию U по переменной y, используя второе равенство системы:
, так как её частная производная по x равна нулю. Далее дифференцируем полученную функцию U по переменной y, используя второе равенство системы: 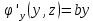
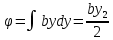 + ѱ(z)
+ ѱ(z)U=
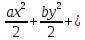 ѱ(z)
ѱ(z)Используя третье уравнение системы:
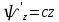
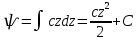
U=
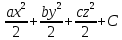
3. Определить величины ∆
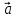 ,
, 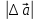 , и ∆
, и ∆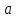 соответствующие изменению направления вектора
соответствующие изменению направления вектора 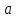 на противоположное.
на противоположное.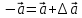
∆
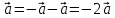
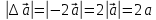
∆

4. Колесо вращается вокруг своей оси симметрии так, что зависимость угла поворота радиуса колеса от времени дается уравнением
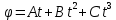 , где А=2 рад/с, В=0,5 рад/с2 , С=0,5рад/с3 . Найти радиус R колеса, если в момент времени t=2 c нормальное ускорение точки на ободе колеса равно
, где А=2 рад/с, В=0,5 рад/с2 , С=0,5рад/с3 . Найти радиус R колеса, если в момент времени t=2 c нормальное ускорение точки на ободе колеса равно 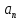 = 36 м/с
= 36 м/с
2.
Дано:
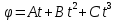
А=2 рад/с
В=0,5 рад/с2
С=0,5рад/с3
t=2 c
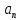 = 36 м/с2
= 36 м/с2R - ?
Решение:
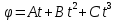
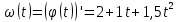
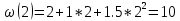
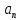 =
=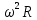
R=
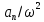
R=36/102=0.36 (м)
Ответ: R=0,36 м
5. Найти для идеального газа уравнение такого процесса, при котором теплоемкость газа изменяется с температурой по закону С=
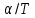 , где
, где 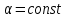 .
.Первое начало (в расчете на 1 моль)
δԚ =
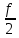 RdT + pdV
RdT + pdVC = a/T =
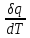 =
= 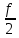 R + p
R + p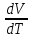
Давление подставим из уравнения состояния
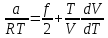
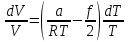
In V =
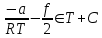
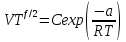
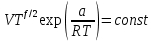 Через уравнение состояния перейдем к p-V представлению
Через уравнение состояния перейдем к p-V представлению