Файл: Равновесие плоской системы сил. Определение реакций опор твердого тела.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 17.03.2024

Просмотров: 53

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Равновесие плоской системы сил. Определение реакций опор твердого тела.

Определить реакции связей для бруса ABC, ось которого - ломаная линия. Размеры бруса, угол между его частями AB и BC, расположение бруса задано. Точка D приложения силы F делит отрезок AB пополам. Способ закрепления бруса указан. Приведены модуль и направление силы F, интенсивность равномерной нагрузки, действующей на отрезок BC, модуль и направление пары сил, действующей на брус.





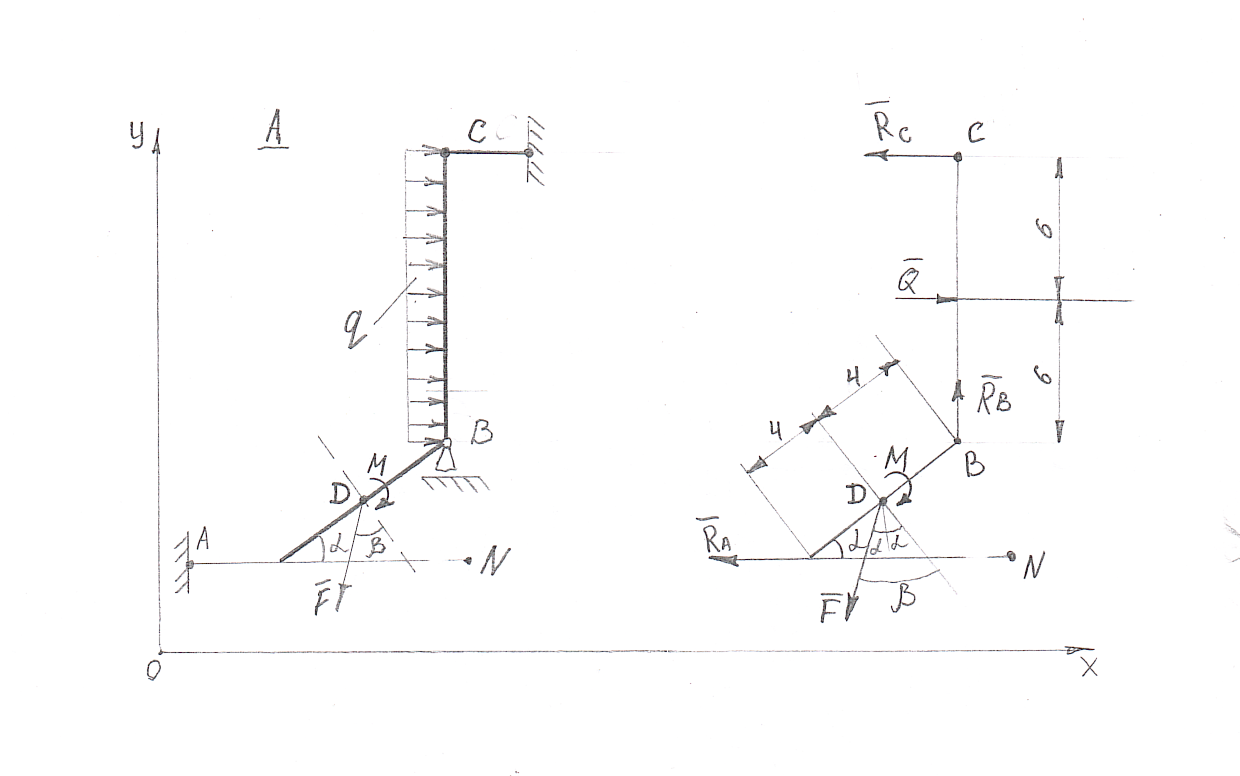
Рисунок 1.1

Дано:

F=6kH,

M=-12kH м,

q=3kH/м,

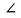ABC= ,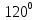

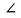NAB=α=+ ,

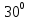AB=8м, BC=12м, угол наклона силы F к вертикали: β=- .

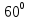Определить:


Ra, Rb, Rc-?

Решение:

Рассматриваем равновесие бруса АDBC(рис.1.1,а). На брус действуют сила F, пара сил с моментом М и равномерно распределенная нагрузка интенсивностью q. Действие этой нагрузки заменяем равнодействующей силой Q=q*BC=3*12=36kH, приложенной посередине нагруженного участка BC. На брус действуют реакция невесомого стержня в точке A, реакция шарнирно подвижной опоры в точке B и реакция невесомого стержня в точке С. Показываем расчетную схему бруса(рис.1.1,б). На брус действует произвольная плоская система сил. Выбираем и показываем оси координат.
Аналитические уравнения равновесия для произвольной плоской системы сил имеют вид:

=0; Q-Ra-F sinα-Rc=0; (1)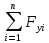

=0; Rb-F cosαα=0; (2)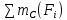

=0; Q
6-M+F cosα 4 cosα-F sinα (12+4 sinα)-Ra (12+8 sinα)=0; (3)
Вычисляем опорные реакции:

Из (2):

Rb=F cosα=6 0.866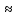 5.196kH;
Из (3):

Ra=(Q 6-M+F cosα 4 cosα-F sinα (12+4 sinα))/(12+8 sinα)=

=(36 6-12+6 0.75 4-6 0.5 (12+4 0.5))/(12+8 0.5)=

=(216-12+18-42)/16=180/16 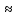11.25kH;
Из (1):

Rc=Q-Ra-F sinα=36-11.25-6 0.5=36-11.25-3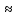 21.75kH;
Для проверки результатов расчета составим уравнение равновесия бруса в виде уравнения моментов сил относительно другой точки
, например A для этого вернёмся к расчётной схеме и составим уравнение моментов сил для шарнира A (рис.1.1,б):
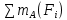=Rb 8 cosα+Rc (8 sinα+12)-Q (8 sinα+6)-M-F cos|β| 4=0;

5.196 8 0.866+21.75 (8 0.5+12)-36 (8 0.5+6)-12-6 0.5 4=0;

36+348-360-12-12=0;
384-384 0;

0 0;
Следовательно, наше решение верное!
Ответ: Ra 11.25kH, Rb 5.196kH, Rc 21.75kH.

Смотрите также файлы