Файл: Контрольная работа По дисциплине Биофизика Вариант студент заочного обучения.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.03.2024
Просмотров: 21
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ имени А.А. ЕЖЕВСКОГО
Факультет энергетический Кафедра электрооборудования и физики
Контрольная работа
По дисциплине «Биофизика»
Вариант ____
Выполнил: студент заочного обучения направления подготовки __________
профиль__________________________
курс______________________________
группа____________________________ ФИО_____________________________
Проверил:_________________________
Молодежный, 2023 г.
108. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны 100 м. Закон движения автомобиля выражается уравнением
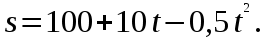 Найти скорость автомобиля, его тангенциальное, нормальное и полное ускорение в конце пятой секунды.
Найти скорость автомобиля, его тангенциальное, нормальное и полное ускорение в конце пятой секунды.Решение: найдем скорость, вычислив производную от уравнения движения.
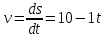
Подставим значение, равное 5 сек, получим
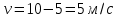
Тангенциальное ускорение найдем, взяв производную от полученного ранее уравнения скорости:
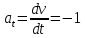 . Видим, что тангенциальное ускорение
. Видим, что тангенциальное ускорение 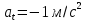
Нормальное ускорение определяется по формуле
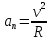 . Подставим найденное значение скорости и значение радиуса по условию, получим:
. Подставим найденное значение скорости и значение радиуса по условию, получим: 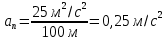
Полное ускорение найдем по формуле:
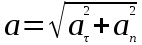 .
.Получим
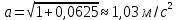
118. Человек массой 70 кг, бегущий со скоростью 9 км/ч, догонят тележку массой 190 кг, движущуюся со скоростью 3,6 км/ч, и вскакивает на нее. С какой скоростью будет двигаться тележка с человеком, если человек до прыжка бежал навстречу тележке?
Решение: чтобы найти необходимую скорость воспользуемся законом сохранения импульса:
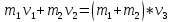 , где
, где 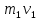
- импульс человека до удара,
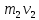 - импульс вагона до прыжка,
- импульс вагона до прыжка, 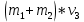 - общий импульс человека и вагона после прыжка.
- общий импульс человека и вагона после прыжка.Так как вагон движется в сторону человека, то, проектирую вектора импульсов на ось X, получаем:
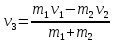
Подставим числа, получим:
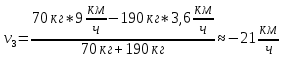
Получили отрицательное число, что говорит нам о том, что вагон с человеком продолжили движение в сторону движения вагона, итоговый ответ:
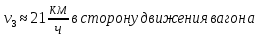
128. Спутник вращается вокруг Земли по круговой орбите радиусом 1700 км. Определить его линейную скорость и период обращения, если радиус Земли равен 6400 км.
Решение: воспользуемся формулой для вычисления первой космической скорости:
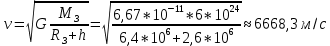
Период обращения вычислим по формуле:
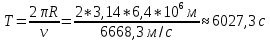
138. Вычислить кинетическую энергию вала диаметром 0,3 м, вращающегося с частотой 200 об/мин, если масса его 2·103 кг.
Решение: кинетическая энергия вращающегося тела относительно неподвижной оси равна
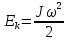 , момент инерции сплошного цилиндра
, момент инерции сплошного цилиндра 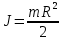 , угловая частота
, угловая частота 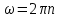 , где n – число оборотов в секунду, также имеем
, где n – число оборотов в секунду, также имеем 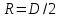 , получим расчетную формулу:
, получим расчетную формулу: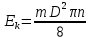
Найдем число оборотов в секунду:
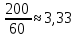
Вычислим кинетическую энергию, получим
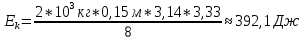
148. Стержень вращается вокруг оси, проходящей через его середину, согласно уравнению
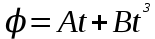 , где А = 2 рад/с, В = 0,2 рад/с3. Определить вращающий момент, действующий на стержень через 2 с после начала вращения, если момент инерции стержня
, где А = 2 рад/с, В = 0,2 рад/с3. Определить вращающий момент, действующий на стержень через 2 с после начала вращения, если момент инерции стержня 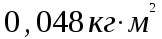 .
.Решение
: Из второго закона Ньютона к вращающимся телам находим
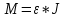 , где M – вращающийся момент,
, где M – вращающийся момент, 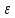 – угловое ускорение, J – момент инерции диска.
– угловое ускорение, J – момент инерции диска.По определению
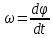 , тогда
, тогда 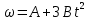 , а
, а 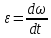 , тогда
, тогда 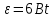 .
.В момент времени t = 2, имеем, что
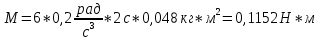
158. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых
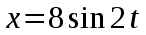 и
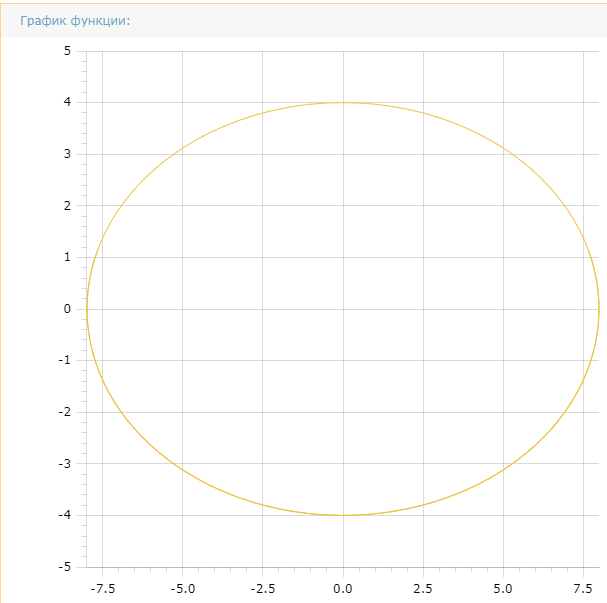
и 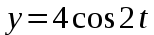 . Написать уравнение траектории и построить ее. Показать направление движения точки.
. Написать уравнение траектории и построить ее. Показать направление движения точки.Решение: параметрическое уравнение эллипса выглядит следующим образом
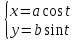
Где a и b – длина полуоси эллипса, в таком случае имеем аналогичное уравнение траектории:
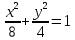
От 2t в данном случае зависит лишь период обращения, в нашем случае период равен
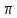 .
. 
Для определения направления движения, возьмем момент времени t =
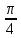 , имеем, что
, имеем, что 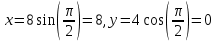 , учитывая, что в при t = 0, имеем x = 0, а y = 4, заключаем, что движение идет по часовой стрелке.
, учитывая, что в при t = 0, имеем x = 0, а y = 4, заключаем, что движение идет по часовой стрелке.208. Вычислить плотность азота, находящегося в баллоне под давлением 2 МПа и имеющего температуру 400 К.
Решение: воспользуемся уравнением Менделеева-Клапейрона, т.к. плотность определяется как
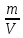 , выразим это из формулы:
, выразим это из формулы: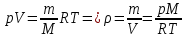
Подставим значения, получим
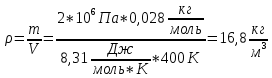
218. Давление идеального газа 10 мПа, концентрация молекул
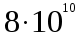
см-3. Определить среднюю кинетическую энергию поступательного движения одной молекулы и температуру газа.
Решение: для начала найдем температуру, используя формулу зависимости давления газа от концентрации и температуры:
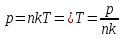
После этого найдем среднюю кинетическую энергию одной молекулы идеального газа по формуле:
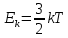
Подставим значения, получим:
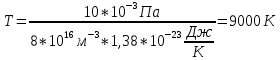
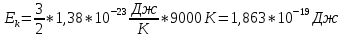
При решении также пользовались
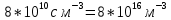
228. Средняя квадратичная скорость некоторого газа при нормальных условиях равна 480 м/с. Сколько молекул содержит 1 г этого газа?
Решение: при нормальных условиях, значит
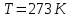 , тогда, воспользуемся формулой средней квадратичной скорости, чтобы найти молярную массу:
, тогда, воспользуемся формулой средней квадратичной скорости, чтобы найти молярную массу: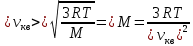
Тогда количество молекул в грамме этого газа будет находиться по формуле:
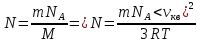
Подставим значения, получим
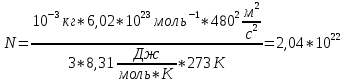
238. Найти молярную массу среды, для которой удельная изобарная теплоемкость сp = 1820 Дж/(
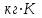 ) и изохорная cv = 1360 Дж/(
) и изохорная cv = 1360 Дж/(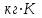 ).
).Решение: молярная теплоемкость газа при постоянном объеме равна
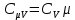 , аналогично при постоянном давлении
, аналогично при постоянном давлении 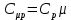
Запишем уравнение Майера:
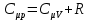
Таким образом можем выразить молярную массу, получим:
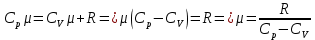
Подставим значения, получим:
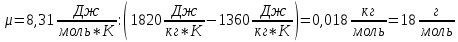
248. Водород массой 4 г был нагрет на
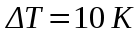 при постоянном давлении. Определить работу расширения газа.
при постоянном давлении. Определить работу расширения газа.Решение: работа при изобарном расширении определяется по формуле:
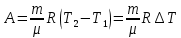
Подставим значения, получим:
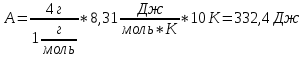
258. Идеальный газ совершает цикл Карно. Газ получил от нагревателя количество теплоты 5,5 кДж и совершил работу 1,1 кДж. Определить: 1) термический КПД цикла; 2) отношение температур нагревателя и холодильника.
Решение: термический КПД цикла определим по формуле:
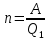
Определим отношение температур, исходя из формулы:
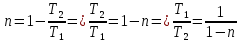
Подставим значения:
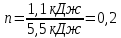
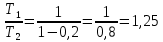
-
Расстояние l между зарядами Q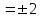 нКл равно 25 см. Определить напряженность Е поля, созданного этими зарядами в точке, находящейся на расстоянии r1 = 15 см от первого и на расстоянии r2 = 20 см от второго заряда.
нКл равно 25 см. Определить напряженность Е поля, созданного этими зарядами в точке, находящейся на расстоянии r1 = 15 см от первого и на расстоянии r2 = 20 см от второго заряда.
Решение: покажем на рисунке.
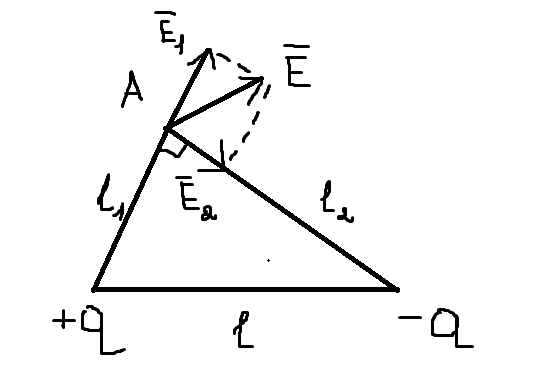
По принципу суперпозиции имеем, что напряженность поля есть сумма векторов E1 и E2, т.е. на рисунке это вектор E, найдем его с помощью теоремы Пифагора:
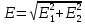
Каждый вектор найдем по формулам:
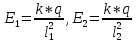
Подставим формулы, получим:
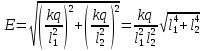
Подставим значения, получим:
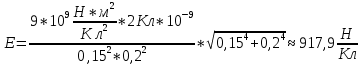
318. Пылинка массой 0,2 мг, несущая на себе заряд Q = 40 нКл, влетела в электрическое поле в направлении силовых линий. После прохождения разности потенциалов U = 200 В пылинка имела скорость
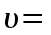 10 м/с. Определить скорость
10 м/с. Определить скорость 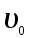 пылинки до того, как она влетела в поле.
пылинки до того, как она влетела в поле.Решение: из закона сохранения энергии имеем:
