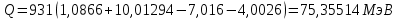Файл: Контрольная работа По дисциплине Биофизика Вариант студент заочного обучения.docx

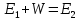
Где 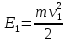- начальная кинетическая энергия пылинки, 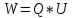– потенциальная энергия пылинки, проходящей через разность потенциалов U, 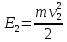– конечная кинетическая энергия пылинки.

Значит имеем, что



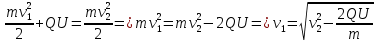
Подставим значения, получим:



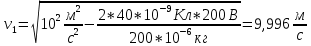
328. Плоский воздушный конденсатор заряжен до разности потенциалов 300 В. Площадь пластин S = 1см², напряженность поля в зазоре между ними Е = 300 кВ/м. Определить поверхностную плотность заряда на пластинах, емкость и энергию конденсатора.
Решение: Напряженность E поля в зазоре между обкладками конденсатора определяется по формулам:



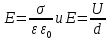
Отсюда,


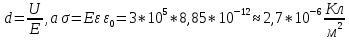
Диэлектрическую проницаемость воздуха взяли равной единице.

Емкость конденсатора найдем по формуле:



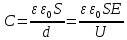
Подставим значения,



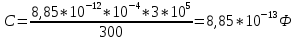
Энергию конденсатора найдем по формуле:



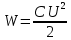
Подставим значения:



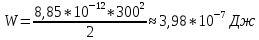
338. Определить плотность тока в железном проводнике длиной 10 м, если провод находится под напряжением 6 В, удельное сопротивление железа 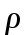= 98 нОм·м.

Решение: сила тока определяется по формул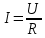е , где 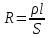, выразим плотность тока.

Плотность тока определим по формуле:



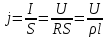
Подставим значения:



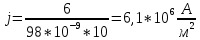
338. ЭДС батареи аккумуляторов равна 12 В, сила тока короткого замыкания равна 5 А. Какую наибольшую мощность можно получить во внешней цепи, соединенной с такой батареей?

---

Решение: полезная мощность, которая выделяется на внешней цепи, можно найти по формуле 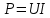, где U – напряжение на внешней цепи, можно найти согласно закону Ома по формуле .

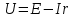Подставим последнюю формулу напряжения в формулу мощности, получим 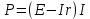, таким образом рассмотрим теперь функцию мощности, которая зависит от силы тока: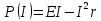



Как видим, данная функцию является параболой, ветви которой направлены вниз, значит её максимум достигается в экстремуме, найдем производную и вычислим значение максимума:



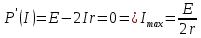
Также знаем, что 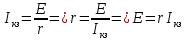, где E – ЭДС источника, а r – внутреннее сопротивление.

Получили 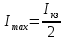, подставим данное значение в функцию мощности, получим,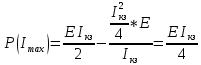



Подставим значения и получим ответ:



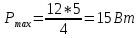
408. По кольцевому медному проводнику протекает ток 30 А. В центре контура с током создается магнитное поле напряженностью 30 А/м. Определить разность потенциалов на концах проводника, если его поперечное сечение 3 мм². Удельное сопротивление меди 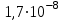Ом·м.
Решение: напряженность магнитного поля в центре кольца определяется формулой

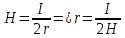
Разность потенциалов 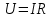, где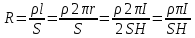

Таким образом выразим,



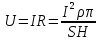
Подставим значения и вычислим,


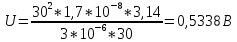
418. Контур из провода, изогнутого в форме квадрата со стороной а = 0,5м, расположен в одной плоскости с бесконечным прямолинейным проводом с током I = 5 А так, что две его стороны параллельны проводу. Сила тока в контуре I₁ = 1 А. Определить силу, действующую на контур, если ближайшая к проводу сторона контура находится на расстоянии

---

b = 10 см.
Решение: покажем на рисунке контур и направление токов.



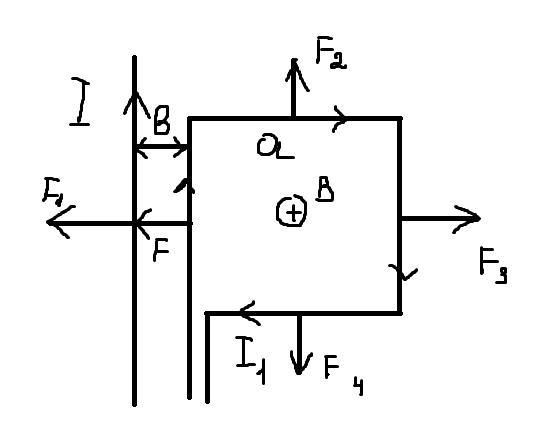
Таким образом видим, что 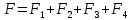, но т.к. 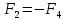, имеем, что 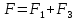, перейдем из векторного вида, получим, что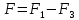



Учитывая, что 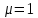, имеем, что 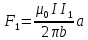, а 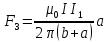, тогда получим в итоге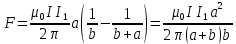



Подставим значения и получим,



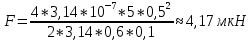
428. В плоскости, перпендикулярной однородному магнитному полю напряженностью 2·10⁵ А/м вращается стержень длиной 0,4 м относительно оси, проходящей через его середину. В стержне индуцируется электродвижущая сила, равная 0,2 В. Определить угловую скорость стержня.
Решение: связь линейной и угловой скорости определяется следующим соотношением
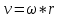
Стержень вращается относительно оси, проходящей через его середину, а значит у разных точек стержня разные радиусы вращения, и следовательно, разная линейная скорость, но, как видим из формулы, скорость линейно зависит от расстояния, потому для нахождения ЭДС возникающей в стержне будем использовать среднюю линейную скорость

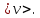
Тогда

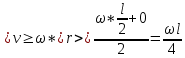
Связь между индукцией и напряженностью магнитного поля

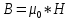
ЭДС

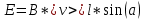
Подставим формулу индукции и средней скорости в формулу ЭДС, получим



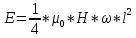
Учитывая, что плоскость вращения стержня перпендикулярна линиям магнитной индукции, то имеем что 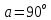, а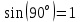

---

Выразим угловую скорость стержня:



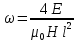
Подставим значения,



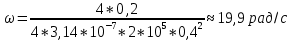
438. На дифракционную решетку, содержащую 500 штрихов на 1 мм, падает в направлении нормали к ее поверхности белый свет. Спектр проецируется помещенной вблизи решетки линзой на экран. Определить ширину спектра первого порядка на экране, если расстояние L от линзы до экрана равно 3 м. Границы видимого спектра λ_кр. = 780 нм, λ_ф = 400 нм.
Решение:



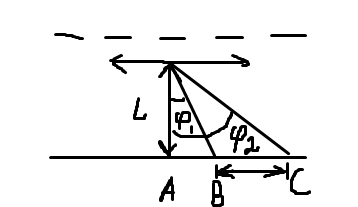
как знаем, , в нашем случае нужно определить ширину спектра первого порядка и потому , значит имеем,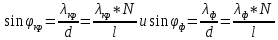



Имеем, что

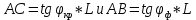
Итого имеем формулу:



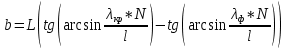
Подставим значения в формулу и решим,


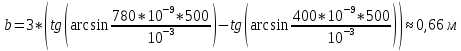
448. На поверхность металла падает монохроматический свет с длиной волны 0,1 мкм. Красная граница фотоэффекта 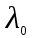= 0,3 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии?

Решение: Формула Эйнштейна для фотоэффекта 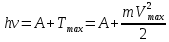, где 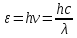– энергия фотона.

Откуда видим, что

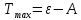
Если V=0, то 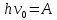, где 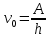- красная граница фотоэффекта.

По определению 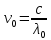, где c – скорость ветра, тогда 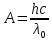– работа выхода из металла.

Тогда

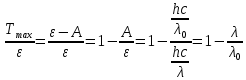
Подставим значения и получим,



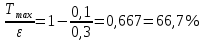
458. Постоянная радиоактивного распада

---

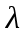для изотопа 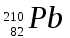равна 10^-9 с^-1. Определить время, в течение которого распадается 2/5 начального количества ядер этого радиоактивного изотопа.

Решение:

2/5 начального количества ядер радиоактивного изотопа распалось, значит осталось 3/5, запишем



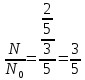
Запишем закон радиоактивного распада:



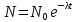
Где λ – постоянная радиоактивного распада.

Выразим t:



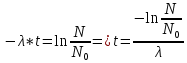
Подставим значения, получим



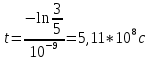
468. Вычислить энергию ядерной реакции

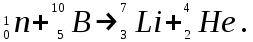
Решение:

Энергия ядерной реакции определяется по формуле:



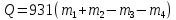
Вычислим массу ядер до реакции и после реакции,

До реакции имеем:



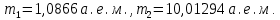
После реакции имеем:



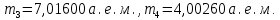
Подставим все значения и вычислим энергию:

---