Файл: Реферат текстовый документ содержит страниц, включая рисунок, таблицы, формулы, источников.docx
Добавлен: 18.03.2024
Просмотров: 40
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
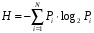 , где N – количество символов, P(i) – вероятность символов, log2P(i) – количество информации по Хартли.
, где N – количество символов, P(i) – вероятность символов, log2P(i) – количество информации по Хартли.Количество «1» равно значению 30. Количество «0» равно значению 25.
Для избыточности источника надо сначала воспользоваться формулой Хартли.
Hмакс = log2N, где N – количество символов.
Затем избыточность источника находится по формуле D = 1 -
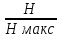

Рисунок 11 – Вероятность двоичных символов, передаваемых по каналу
H = 0,994
Hмакс = log22 = 1
D = 1 –
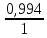 = 0,006
= 0,006Скорость передачи информации I’ по каналу без помех определяется только временем передачи одного кодового символа (равным длительности посылки τ), средней длиной кодового слова µ и средним количеством информации, заключенной в кодовом слове, равным энтропии H(A) исходного источника
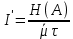
H(A) = 3,55
τ = 1,1 мкс = 0.0000011 секунд
Средняя длина кодового слова рассчитывается по формуле
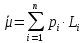 , отсюда
, отсюда 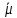 =0,153*3+0,119*4+0,111*4+0,11*4+0,091*4+0,082*3+0,078*5+0,068*5+0,067*4+0,027*4+0,024*4+0,024*4+0,023*4+0,022*3=3,885
=0,153*3+0,119*4+0,111*4+0,11*4+0,091*4+0,082*3+0,078*5+0,068*5+0,067*4+0,027*4+0,024*4+0,024*4+0,023*4+0,022*3=3,885Отсюда, скорость передачи информации I’ =
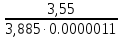 = 1*
= 1*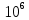
бит/с.
3 Информационные характеристики источника и эффективного кода
3.1 Энтропия и избыточность источника
Главными информационными характеристиками источника являются энтропия и избыточность.
Энтропия источника рассчитана по формуле (1):
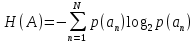 , (1)
, (1)где N – объем алфавита;
p(an) – априорная вероятность n-того символа.
Произведен расчет исходя из данных таблицы 1.
H(A)=-(0,091*LOG(0,091;2) + 0,024*LOG(0,024;2) + 0,067*LOG(0,067;2) + 0,082*LOG(0,082;2) + 0,119*LOG(0,119;2) + 0,027*LOG(0,027;2) + 0,078*LOG(0,078;2) + 0,111*LOG(0,111;2) + 0,023*LOG(0,023;2) + 0,022*LOG(0,022;2) + 0,11*LOG(0,11;2) + 0,068*LOG(0,068;2) + 0,153*LOG(0,153;2) + 0,024*LOG(0,024;2))= 3,55005 (2)
Таким образом, для рассматриваемого источника энтропия равна 3,641 бит. Максимальная же энтропия рассчитана по формуле (3).
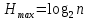 , (3)
, (3)где n – количество символов в алфавите.
Тогда для данного источника максимальная энтропия равна (4):
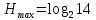 = 3,8074 бит. (4)
= 3,8074 бит. (4)Избыточность источника вычисляется по формуле (5):
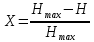 (5)
(5)Рассчитана избыточность источника исходя из полученных данных в формулах (2) и (4):
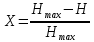 =
= 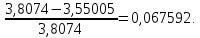 (6)
(6)Расчеты говорят о малой избыточности источника, что является как положительным, так и отрицательным фактом. С увеличением избыточности возрастают показатели помехоустойчивости, однако для передачи сообщения такого сообщения требуется больше времени, поэтому для рассматриваемого источника время передачи стремится к минимально возможному, а помехоустойчивость невысока.
3.2 Характеристики кода
Средняя длина кодовой комбинации рассчитана по формуле (7):
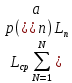 , (7)
, (7)где Ln – длина кодовой комбинации, соответствующей символу;
an – символ из алфавита размером n.
Средняя длина кодовой комбинации равна (8): Lср =3*(0,153+0,082+0,022)+4*(0,119+0,111+0,11+0,091+0,067+0,027+0,024+0,024+0,023)+5*(0,078+0,068) = 3,885 символа. (8)
Определена вероятность появления символов 0 и 1 в кодовых комбинациях. Вероятность появления единицы находится как сумма количеств единиц во всех кодовых словах с весами, равными вероятностям кодовых слов, отнесённая к средней длине кодового слова (9):
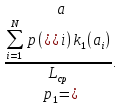 (9)
(9)Тогда для имеющихся данных вероятность появления единицы будет равна (10):
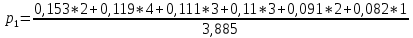 +
+ 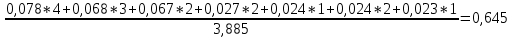 (10)
(10)Вероятность появления нуля находится как сумма количеств нулей во всех кодовых словах с весами, равными вероятностям кодовых слов, отнесённая к средней длине кодового слова (11):
 (11)
(11)Тогда для имеющихся данных вероятность появления нуля равна (12):
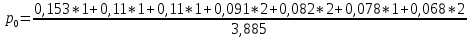 +
+ 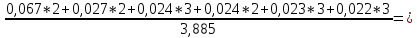 0,354 (12)
0,354 (12)Энтропия кода рассчитана по формуле (13):
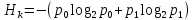 бит. (13)
бит. (13)С учетом полученных вероятностей (10) и (12) рассчитана энтропия кода (14):
 (14)
(14)Избыточность кода рассчитывается по формуле (15):
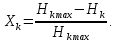 (15)
(15)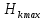 = 0.938, тогда с учетом найденного Hк (16):
= 0.938, тогда с учетом найденного Hк (16):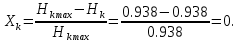 (16)
(16)Скорость передачи информации по каналу без помех рассчитывается по формуле (17):
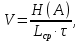 (17) где
(17) где 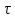 – длительность посылки.
– длительность посылки.Т.к. τ = 1.1 мкс по условию, получена скорость передачи (18):
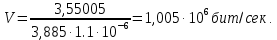
(18)
Скорость зависит не только от свойств самого канала, но и от подаваемого на его вход сигнала, поэтому не может характеризовать канал.
4 Демодуляция методом однократного отсчета
4.1 Когерентный прием. Определение порога, расчет условных вероятностей ошибок, средней вероятности ошибки, скорости передачи информации
Все методы приема, для реализации которых необходимо точное априорное знание начальных фаз приходящих сигналов, называют когерентными. Если в линии только шум с нулевым средним (гипотеза Н0), то на выходе канала связи есть сигнал с Гауссовой плотностью распределения (19):
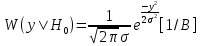 (19)
(19)где
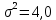 – дисперсия шума.
– дисперсия шума.Если в линии сумма сигнала и шума (гипотеза Н1), то на выходе канала связи есть сигнал с Гауссовой плотностью распределения (20):
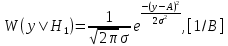 (20)
(20) где А =
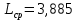 – средняя длина символа;
– средняя длина символа;σ2 = 4,0 – дисперсия шума.
Графики плотности распределения вероятностей мгновенных значений колебания на входе демодулятора при приеме посылки и паузы – рисунок 12.
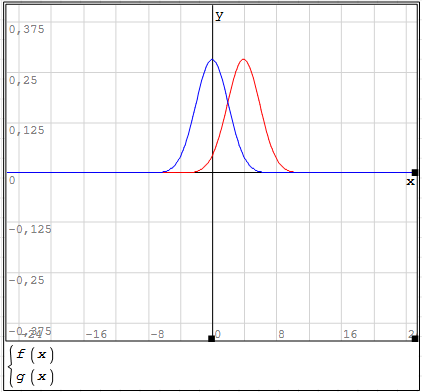
Рисунок 12 – Гауссовая плотность распределения: синим сплошным – шум с нулевым средним (гипотеза Н0); зеленым пунктиром – сумма сигнала и шума (гипотеза Н1); черным пунктиром – пороговое значения yп при когерентном приёме
Оптимальный порог по критерию идеального наблюдателя для принятия решения о принимаемом символе найдена как абсцисса пересечения условных плотностей распределения вероятностей, умноженных на априорные вероятности гипотез (21) – (23):
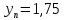 (21)
(21)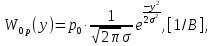 (22)
(22)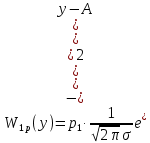 (23)
(23) Условная вероятность ошибки первого рода (24) – ложной тревоги (передавалась единица, а принят ноль):
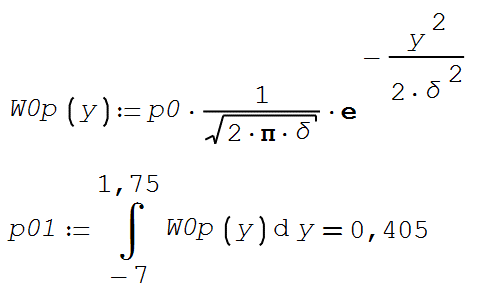
Условная вероятность ошибки второго рода (25) – пропуск сигнала (передался ноль, а принята единица):
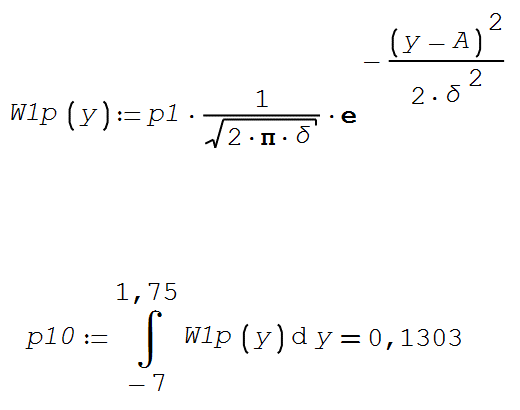
Средняя вероятность ошибки (26):
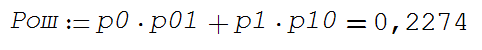 (26)
(26)где p01 – вероятность получения «1» при передаче «0»;
p10 – вероятность получения «0» при передаче «1».
Скорости передачи информации при наличии помех равна (27):
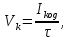 (27)
(27)где
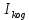 – среднее количество передаваемой по каналу информации;
– среднее количество передаваемой по каналу информации; τ – длительность посылки.
Безусловные вероятности выходных символов для нахождения энтропии источника (28) – (31):
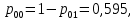 (28)
(28)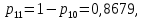 (29)
(29)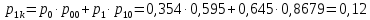 (30)
(30)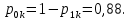 (31)
(31)Энтропия источника (32):
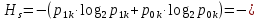 (0,12 ∙ log20.12 + 0,88∙ ∙ log20.88) = 0.77 бит.
(0,12 ∙ log20.12 + 0,88∙ ∙ log20.88) = 0.77 бит.Энтропия источника, рассчитанная ранее Hk = 0.938 бит, тогда совместная энтропия входа и выхода канала равна (33):
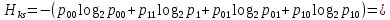
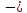 (0.595) ≈ 1.53 бит. (33)
(0.595) ≈ 1.53 бит. (33)Среднее количество передаваемой по каналу информации (приходящееся на один символ) равно (34):
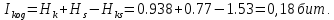 (34)
(34)Скорость передачи информации при наличии помех (35):
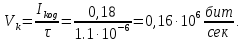 (35)
(35)4.2 Некогерентный прием. Определение порога, расчет условных вероятностей ошибок, средней вероятности ошибки, скорости передачи информации
Условная плотность распределения вероятностей суммы сигнала и шума (36):
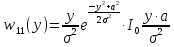 (36)
(36)где I0(*) – модифицированная функция Бесселя первого рода нулевого порядка. Для определения оптимального по критерию идеального наблюдателя порога необходимо рассчитать условные плотности распределения вероятностей, умноженные на априорные вероятности гипотез H0 и H1 (37) – (39):
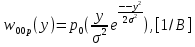 (37)
(37)