Файл: Реферат текстовый документ содержит страниц, включая рисунок, таблицы, формулы, источников.docx
Добавлен: 18.03.2024
Просмотров: 38
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(38)
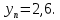 (39)
(39)
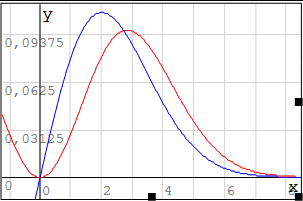
Рисунок 13 – Плотность распределения при некогерентном приеме: синим сплошным – шум с нулевым средним (гипотеза Н0); зеленым пунктиром – сумма сигнала и шума (гипотеза Н1); черным пунктиром – пороговое значения yп при некогерентном приёме
Условная вероятность ошибки первого рода (ложная тревога) (40):
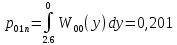 (40)
(40)
Условная вероятность ошибки второго рода (пропуск сигнала) (41):
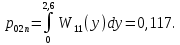 (41)
(41)
Средняя вероятность ошибки (42):
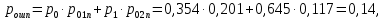 (42)
(42)
Определение скорости передачи информации при некогерентном приеме (43) – (46):
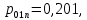 (43)
(43)
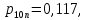 (44)
(44)
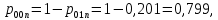 (45)
(45)
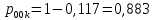 (46)
(46)
Совместные вероятности сочетаний входных и выходных символов (47) – (50):
P02
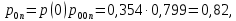 (47)
(47)
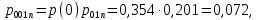 (48)
(48)
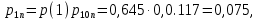 (49)
(49)
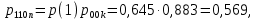 (50)
(50)
Безусловные вероятности выходных символов для нахождения энтропии источника (51), (52):
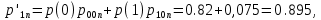 (51)
(51)
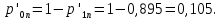 (52)
(52)
Энтропия источника равна (53):
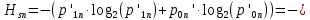 (0,51875 ∙ log20,51875 + 0,48125log20,48125) = 0,49 бит (53)
(0,51875 ∙ log20,51875 + 0,48125log20,48125) = 0,49 бит (53)
Энтропия источника, рассчитанная ранее: Hk=0,938 бит. Совместная энтропия входа и выхода цифрового канала (54):
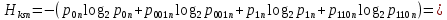
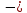 (0,448log20,448 + 0,052log20,052 + 0,42925log20,42925 + 0,07075log20,07075) = 1,25 бит. (54)
(0,448log20,448 + 0,052log20,052 + 0,42925log20,42925 + 0,07075log20,07075) = 1,25 бит. (54)
Среднее количество передаваемой информации по каналу (55):
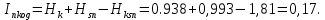
(55)
Скорость передачи информации при наличии помех (56):
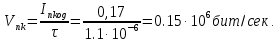 (56)
(56)
Анализируя полученные результаты, сделан вывод о том, что для канала связи с помехами режим когерентного приёма обеспечивает меньшие вероятности возникновения ошибок и большую скорость передачи, чем режим некогерентного при
5 Согласованный фильтр
В случае приёма сигнала известной формы демодулятор должен вычислить значение корреляционного интеграла, которое сравнивается с порогом, выбираемым в соответствии с принятым критерием эффективности. Устройство, вычисляющее корреляционный интеграл, называется коррелятором.
Коррелятор является нестационарным (параметрическим) устройством и включает генератор опорного колебания, совпадающего по форме с ожидаемым сигналом на интервале наблюдения, и интегратор, на выходе которого в момент окончания интервала наблюдения формируется значение, сравниваемое с порогом. В некоторых случаях удобнее использовать ЛИС-цепь, которая вычисляет значение корреляционного интеграла и называется согласованным фильтром. Он играет роль детектора и рассчитывается для обнаружения сигнала заранее известной формы, выходной сигнал фильтра при этом не совпадает по форме ни с входным, ни с сигналом, для обнаружения которого фильтр предназначен. Согласованный фильтр (СФ) для прямоугольного радиоимпульса имеет импульсную характеристику в виде такого же радиоимпульса, обращенного во времени (зеркальной копии). Модуль комплексной частотной характеристики СФ с точностью до произвольного постоянного множителя ψ совпадает с модулем спектральной плотности сигнала, аргумент КЧХ совпадает с аргументом спектральной плотности сигнала, взятым с минусом. Действие СФ на аддитивную смесь сигнала с шумом можно рассмотреть по отдельности в силу линейности фильтра. Отклик СФ на «свой» сигнал в момент максимума численно равен энергии сигнала. Для нахождения дисперсии шума на выходе СФ нужно умножить СПМ входного шума на квадрат модуля КЧХ СФ и затем проинтегрировать по частоте. Согласованный фильтр обеспечивает максимальное отношение сигнал/шум на выходе, тем самым максимизируя потенциальную вероятность правильных решений демодулятора.
На вход фильтра поступает смесь гауссова шума с заданной дисперсией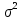
и радиоимпульса с известными огибающей, длительностью, частотой заполнения и начальной фазой.
s(t) = Acos(????0t+φ0), (31)
где A – амплитуда, В;
w0 – частота, Гц;
0 – начальная фаза.
Этот фильтр, как и любая ЛИС-цепь, исчерпывающим образом описывается импульсной характеристикой hсф(t), при этом выходной сигнал определяется свёрткой (интегралом Дюамеля), которая для момента t0 сравнения с порогом равна.
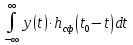
А с учётом финитности.
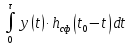
Учитывая, что в момент t0 на выходе согласованного фильтра должно быть выработано значение корреляционного интеграла, приходим к выводу, что должно выполняться равенство.
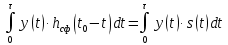 , (32)
, (32)
где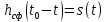 .
.
Исходя из этого, можно сделать вывод, что.
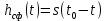 (33)
(33)
где s(t) – посылка (прямоугольный радиоимпульс).
Таким образом, импульсная характеристика согласованного фильтра совпадает по форме с ожидаемым сигналом, обращённым во времени и задержанным на время t0. Для выполнения требования каузальности необходимо, чтобы t0 было не меньше, чем τ.
Зная импульсную характеристику фильтра можно найти КЧХ согласованного фильтра.
5.1 Определение импульсной и комплексной частотной характеристик согласованного фильтра
Рассмотрим фильтр для принятия элементарной посылки. На вход фильтра поступает смесь гауссова шума, с заданной дисперсией 2, и радиоимпульса, с известными огибающей, длительностью, частотой заполнения и начальной фазой (когерентный приём).
Для нашего радиоимпульса.
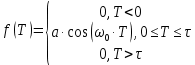 (34)
(34)
a = 7
= 1.110-6
где a – амплитуда, В;
τ – длительность, с;
ω0 – частота заполнения, Гц.
Заполнение высокочастотное, поэтому примем ????0= 2π5 MГц.
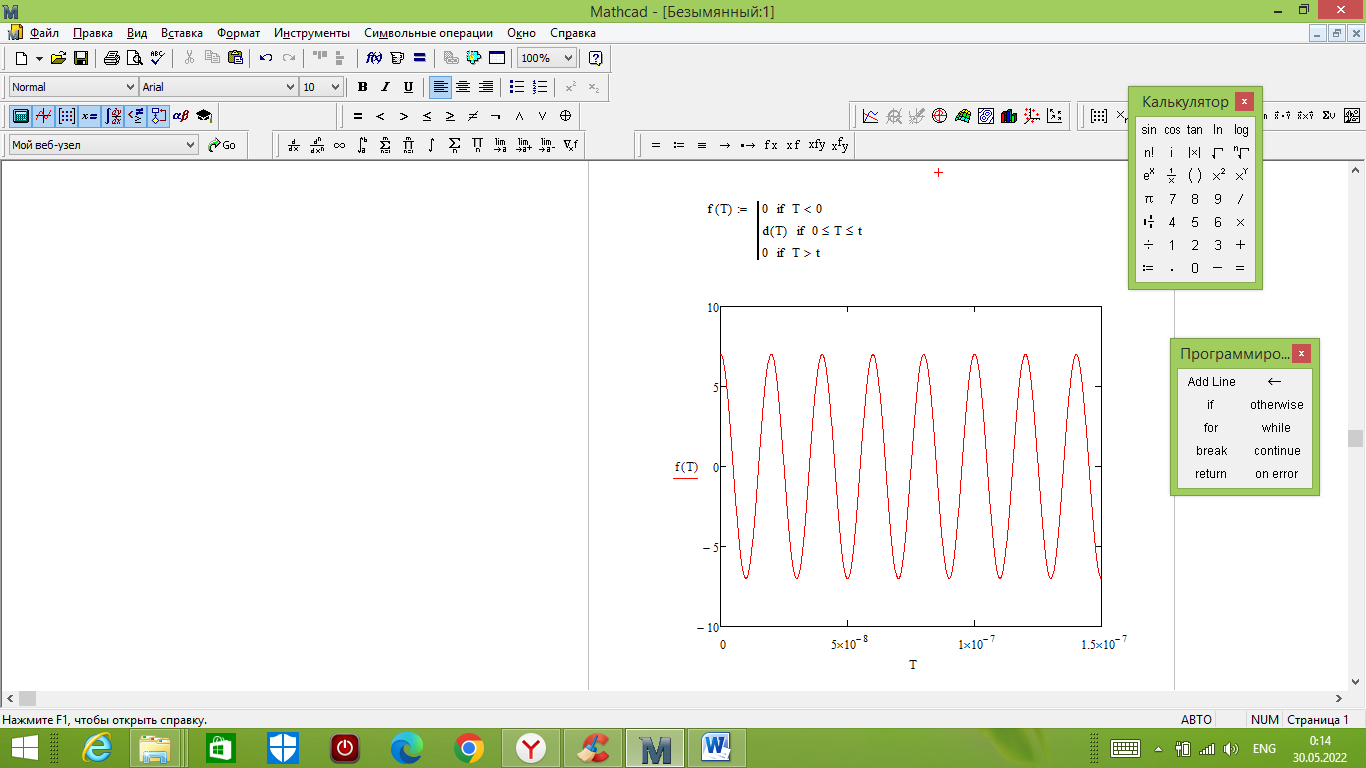
Рисунок 15 – Сигнал на входе согласованного фильтра
Тогда импульсная характеристика такого фильтра будет представлять собой зеркальное отображение временной функции сигнала, задержанное на время, не менее длительности сигнала.
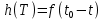 (35)
(35)
где t0– величина не меньше τ.
Примем t0 равным
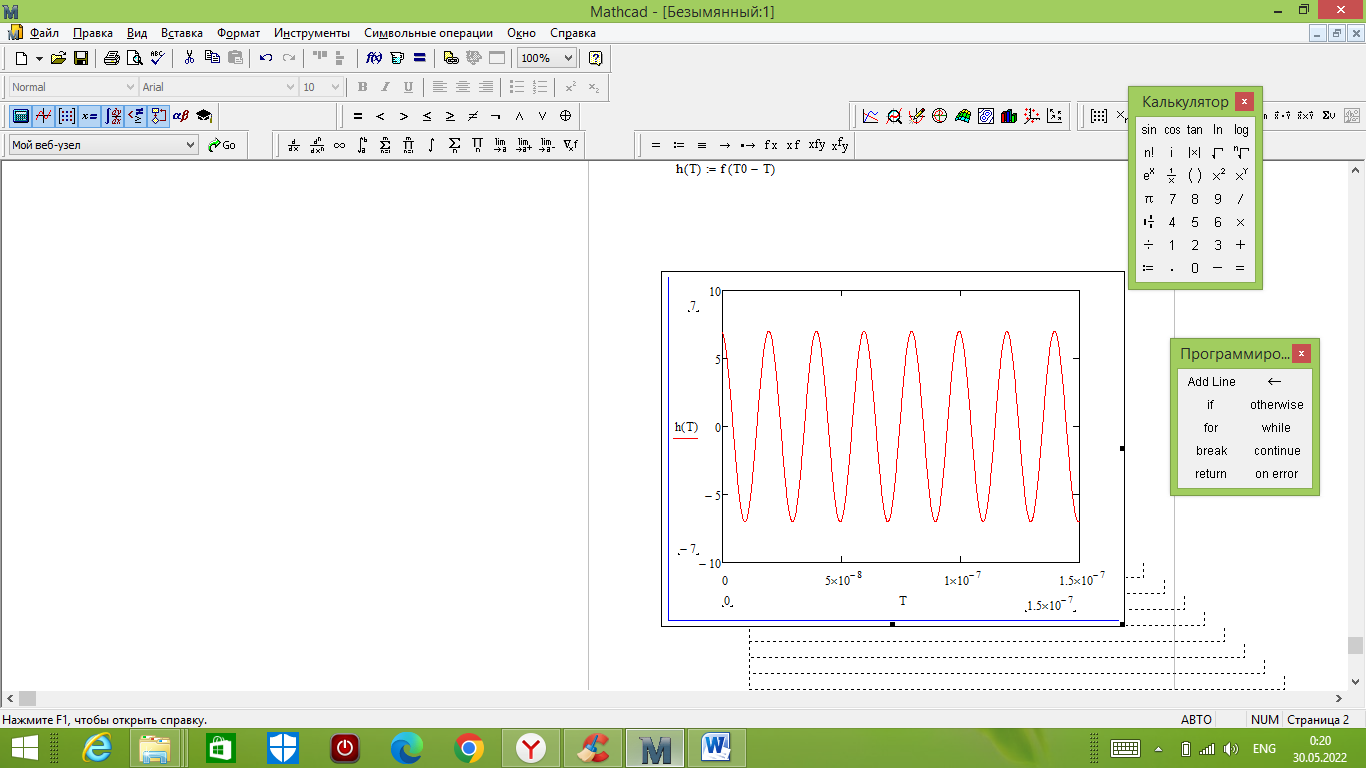
Рисунок 16 – Импульсная характеристика согласованного фильтра
Для нахождения КЧХ фильтра необходимо определить спектральную плотность посылки. Используем прямое преобразование Фурье и теорему сдвига.
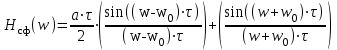 (36)
(36)
Тогда амплитудно-частотная характеристика согласованного фильтра будет выглядеть так.
Рисунок 17 – АЧХ согласованного фильтра
Отклик согласованного фильтра на посылку будет определяется по формуле 37.
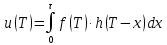 (37)
(37)
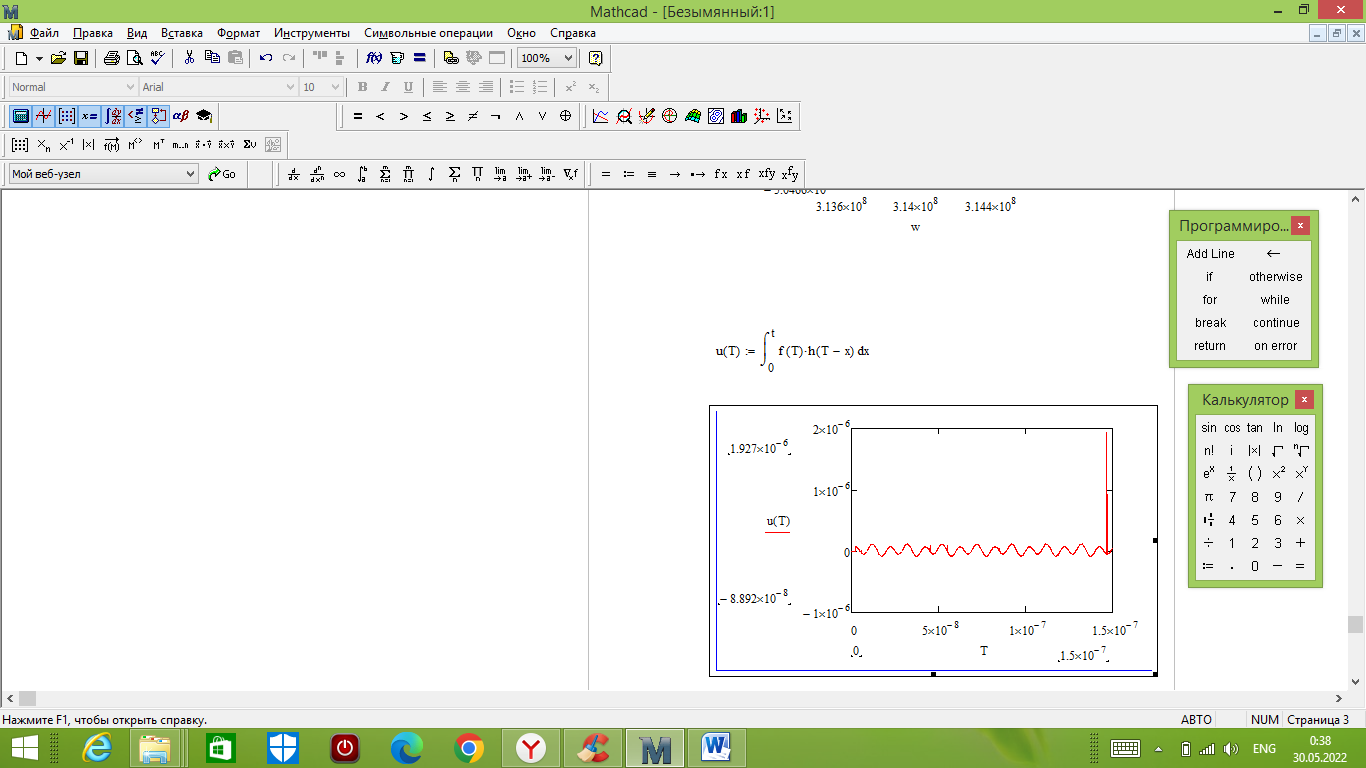
Рисунок 18 – Отклик на выходе согласованного фильтра
Отклик фильтра будет по форме отличаться от исходного сигнала. Дело в том, что от фильтра не требуется передать форму сигнала, а нужно создать максимальный всплеск в момент времени t = .
Значение отклика максимально и численно равно энергии сигнала.
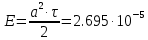 (38)
(38)
Это можно объяснит тем, что отклик представляет собой АКФ посылки, которая достигает максимума, равного энергии сигнала, при нулевом значении аргумента.
5.2 Вычисление условных вероятностей ошибок, средней вероятности ошибки при когерентном приеме с использованием согласованного фильтра, скорости передачи информации
Для определения условных вероятностей ошибки и средней вероятности ошибки при когерентном приеме с использованием согласованного фильтра необходимо найти дисперсию шума на выходе и рассмотреть гауссовы плотности распределения вероятностей.
Помеха это квазибелый шум с нулевым средним, а значит имеет следующую СПМ.
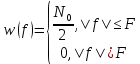
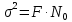
Учитывая, что в данной полосе частот содержится 99% энергии сигнала, найдем F по формуле 39.
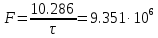 Гц (39)
Гц (39)
F = 9.35110
6 Гц – полоса частот, в которой сосредоточена мощность шума.
Найдём N.
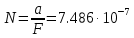 (40)
(40)
Теперь можем найти СКО на выходе согласованного фильтра.
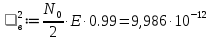 (41)
(41)
Зная СКО на выходе, можно определить и построить ПРВ на выходе согласованного фильтра.
Условная ПРВ для гипотезы H0 – только шум на выходе согласованного фильтра.
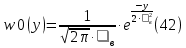
Условная ПРВ для гипотезы H1 – шум/сигнал на выходе согласованного фильтра.
э
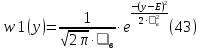
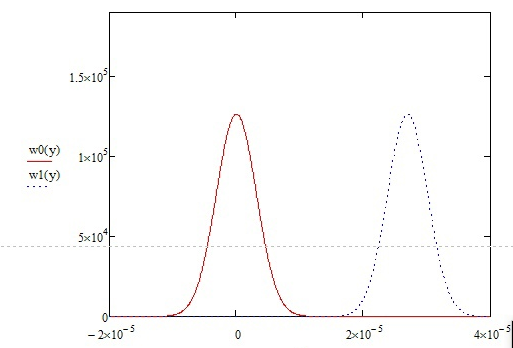
Рисунок 19 – График ПРВ на выходе согласованного фильтра
В данном случае порог равен уп = 0.000013 В. Зная порог, определим условные вероятности ошибок.
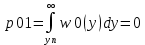
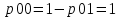
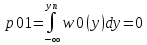
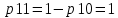
Найдем среднюю вероятность ошибки.
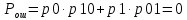
Для наглядности сравним полученные средние вероятности ошибок в таблице 2.
Таблица 2 – Средние вероятности ошибок
По расчётам в Mathcad условные ошибки равны 0. Это означает, что ими можно пренебречь. Тогда средняя ошибка тогда также будет равна 0.
Для нахождения скорости передачи информации найдём среднее количество передаваемой по каналу информации (приходящееся на один символ):
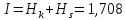 , (44)
, (44)
где Hk – энтропия на входе модулятора;
Hs – энтропия на выходе демодулятора в системе с СФ.
Так как условные вероятности ошибки равны 0, то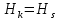 , и скорость передачи с СФ будет равна скорости без шумов:
, и скорость передачи с СФ будет равна скорости без шумов:
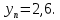 (39)
(39) 
Рисунок 13 – Плотность распределения при некогерентном приеме: синим сплошным – шум с нулевым средним (гипотеза Н0); зеленым пунктиром – сумма сигнала и шума (гипотеза Н1); черным пунктиром – пороговое значения yп при некогерентном приёме
Условная вероятность ошибки первого рода (ложная тревога) (40):
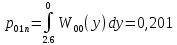 (40)
(40)Условная вероятность ошибки второго рода (пропуск сигнала) (41):
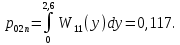 (41)
(41)Средняя вероятность ошибки (42):
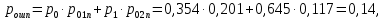 (42)
(42)Определение скорости передачи информации при некогерентном приеме (43) – (46):
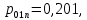 (43)
(43)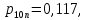 (44)
(44)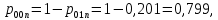 (45)
(45)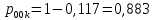 (46)
(46)Совместные вероятности сочетаний входных и выходных символов (47) – (50):
P02
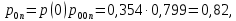 (47)
(47)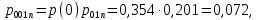 (48)
(48)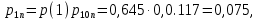 (49)
(49)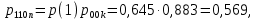 (50)
(50)Безусловные вероятности выходных символов для нахождения энтропии источника (51), (52):
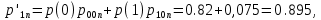 (51)
(51)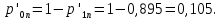 (52)
(52)Энтропия источника равна (53):
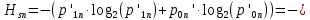 (0,51875 ∙ log20,51875 + 0,48125log20,48125) = 0,49 бит (53)
(0,51875 ∙ log20,51875 + 0,48125log20,48125) = 0,49 бит (53)Энтропия источника, рассчитанная ранее: Hk=0,938 бит. Совместная энтропия входа и выхода цифрового канала (54):
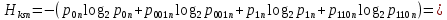
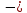 (0,448log20,448 + 0,052log20,052 + 0,42925log20,42925 + 0,07075log20,07075) = 1,25 бит. (54)
(0,448log20,448 + 0,052log20,052 + 0,42925log20,42925 + 0,07075log20,07075) = 1,25 бит. (54)Среднее количество передаваемой информации по каналу (55):
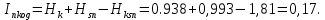
(55)
Скорость передачи информации при наличии помех (56):
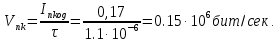 (56)
(56)Анализируя полученные результаты, сделан вывод о том, что для канала связи с помехами режим когерентного приёма обеспечивает меньшие вероятности возникновения ошибок и большую скорость передачи, чем режим некогерентного при
5 Согласованный фильтр
В случае приёма сигнала известной формы демодулятор должен вычислить значение корреляционного интеграла, которое сравнивается с порогом, выбираемым в соответствии с принятым критерием эффективности. Устройство, вычисляющее корреляционный интеграл, называется коррелятором.
Коррелятор является нестационарным (параметрическим) устройством и включает генератор опорного колебания, совпадающего по форме с ожидаемым сигналом на интервале наблюдения, и интегратор, на выходе которого в момент окончания интервала наблюдения формируется значение, сравниваемое с порогом. В некоторых случаях удобнее использовать ЛИС-цепь, которая вычисляет значение корреляционного интеграла и называется согласованным фильтром. Он играет роль детектора и рассчитывается для обнаружения сигнала заранее известной формы, выходной сигнал фильтра при этом не совпадает по форме ни с входным, ни с сигналом, для обнаружения которого фильтр предназначен. Согласованный фильтр (СФ) для прямоугольного радиоимпульса имеет импульсную характеристику в виде такого же радиоимпульса, обращенного во времени (зеркальной копии). Модуль комплексной частотной характеристики СФ с точностью до произвольного постоянного множителя ψ совпадает с модулем спектральной плотности сигнала, аргумент КЧХ совпадает с аргументом спектральной плотности сигнала, взятым с минусом. Действие СФ на аддитивную смесь сигнала с шумом можно рассмотреть по отдельности в силу линейности фильтра. Отклик СФ на «свой» сигнал в момент максимума численно равен энергии сигнала. Для нахождения дисперсии шума на выходе СФ нужно умножить СПМ входного шума на квадрат модуля КЧХ СФ и затем проинтегрировать по частоте. Согласованный фильтр обеспечивает максимальное отношение сигнал/шум на выходе, тем самым максимизируя потенциальную вероятность правильных решений демодулятора.
На вход фильтра поступает смесь гауссова шума с заданной дисперсией
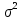
и радиоимпульса с известными огибающей, длительностью, частотой заполнения и начальной фазой.
s(t) = Acos(????0t+φ0), (31)
где A – амплитуда, В;
w0 – частота, Гц;
0 – начальная фаза.
Этот фильтр, как и любая ЛИС-цепь, исчерпывающим образом описывается импульсной характеристикой hсф(t), при этом выходной сигнал определяется свёрткой (интегралом Дюамеля), которая для момента t0 сравнения с порогом равна.
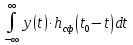
А с учётом финитности.
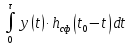
Учитывая, что в момент t0 на выходе согласованного фильтра должно быть выработано значение корреляционного интеграла, приходим к выводу, что должно выполняться равенство.
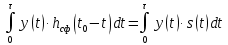 , (32)
, (32)где
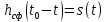 .
.Исходя из этого, можно сделать вывод, что.
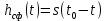 (33)
(33)где s(t) – посылка (прямоугольный радиоимпульс).
Таким образом, импульсная характеристика согласованного фильтра совпадает по форме с ожидаемым сигналом, обращённым во времени и задержанным на время t0. Для выполнения требования каузальности необходимо, чтобы t0 было не меньше, чем τ.
Зная импульсную характеристику фильтра можно найти КЧХ согласованного фильтра.
5.1 Определение импульсной и комплексной частотной характеристик согласованного фильтра
Рассмотрим фильтр для принятия элементарной посылки. На вход фильтра поступает смесь гауссова шума, с заданной дисперсией 2, и радиоимпульса, с известными огибающей, длительностью, частотой заполнения и начальной фазой (когерентный приём).
Для нашего радиоимпульса.
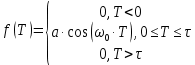 (34)
(34)a = 7
= 1.110-6
где a – амплитуда, В;
τ – длительность, с;
ω0 – частота заполнения, Гц.
Заполнение высокочастотное, поэтому примем ????0= 2π5 MГц.

Рисунок 15 – Сигнал на входе согласованного фильтра
Тогда импульсная характеристика такого фильтра будет представлять собой зеркальное отображение временной функции сигнала, задержанное на время, не менее длительности сигнала.
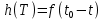 (35)
(35)где t0– величина не меньше τ.
Примем t0 равным

Рисунок 16 – Импульсная характеристика согласованного фильтра
Для нахождения КЧХ фильтра необходимо определить спектральную плотность посылки. Используем прямое преобразование Фурье и теорему сдвига.
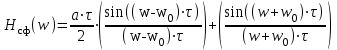 (36)
(36)Тогда амплитудно-частотная характеристика согласованного фильтра будет выглядеть так.
Рисунок 17 – АЧХ согласованного фильтра
Отклик согласованного фильтра на посылку будет определяется по формуле 37.
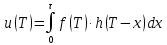 (37)
(37)
Рисунок 18 – Отклик на выходе согласованного фильтра
Отклик фильтра будет по форме отличаться от исходного сигнала. Дело в том, что от фильтра не требуется передать форму сигнала, а нужно создать максимальный всплеск в момент времени t = .
Значение отклика максимально и численно равно энергии сигнала.
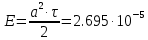 (38)
(38)Это можно объяснит тем, что отклик представляет собой АКФ посылки, которая достигает максимума, равного энергии сигнала, при нулевом значении аргумента.
5.2 Вычисление условных вероятностей ошибок, средней вероятности ошибки при когерентном приеме с использованием согласованного фильтра, скорости передачи информации
Для определения условных вероятностей ошибки и средней вероятности ошибки при когерентном приеме с использованием согласованного фильтра необходимо найти дисперсию шума на выходе и рассмотреть гауссовы плотности распределения вероятностей.
Помеха это квазибелый шум с нулевым средним, а значит имеет следующую СПМ.
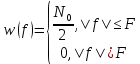
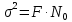
Учитывая, что в данной полосе частот содержится 99% энергии сигнала, найдем F по формуле 39.
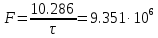 Гц (39)
Гц (39)F = 9.35110
6 Гц – полоса частот, в которой сосредоточена мощность шума.
Найдём N.
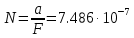 (40)
(40)Теперь можем найти СКО на выходе согласованного фильтра.
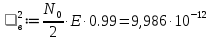 (41)
(41)Зная СКО на выходе, можно определить и построить ПРВ на выходе согласованного фильтра.
Условная ПРВ для гипотезы H0 – только шум на выходе согласованного фильтра.
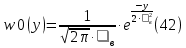
Условная ПРВ для гипотезы H1 – шум/сигнал на выходе согласованного фильтра.
э
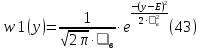

Рисунок 19 – График ПРВ на выходе согласованного фильтра
В данном случае порог равен уп = 0.000013 В. Зная порог, определим условные вероятности ошибок.
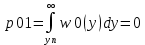
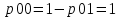
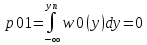
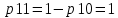
Найдем среднюю вероятность ошибки.
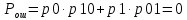
Для наглядности сравним полученные средние вероятности ошибок в таблице 2.
Таблица 2 – Средние вероятности ошибок
| При когерентном приеме | При некогерентном приеме | При использовании согласованного фильтра |
| р =0.227 | р = 0.14 | р = 0 |
По расчётам в Mathcad условные ошибки равны 0. Это означает, что ими можно пренебречь. Тогда средняя ошибка тогда также будет равна 0.
Для нахождения скорости передачи информации найдём среднее количество передаваемой по каналу информации (приходящееся на один символ):
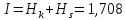 , (44)
, (44)где Hk – энтропия на входе модулятора;
Hs – энтропия на выходе демодулятора в системе с СФ.
Так как условные вероятности ошибки равны 0, то
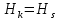 , и скорость передачи с СФ будет равна скорости без шумов:
, и скорость передачи с СФ будет равна скорости без шумов:
