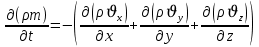ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.03.2024
Просмотров: 38
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Верхняя граница наиболее полно изучена. Здесь отклонения, вызванные проявлением инерционных сил при увеличении скорости фильтрации.
Число Рейнольдса Re:
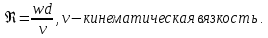
Попытки не увенчались успехом, у всех получилось свое критическое значение числа Рейнольдса.
Нелинейные законы фильтрации
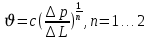
При n=2 получаем формула Краснопольского:
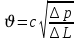
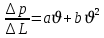
где, a и b – параметры, которые определяются экспериментально или по формулам справочных материалов. При малых скоростях:
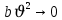
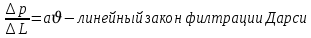
Вторя форма записи более физически обоснованная, потому что скорости фильтрации величины малые.
Обобщенный закон Дарси
О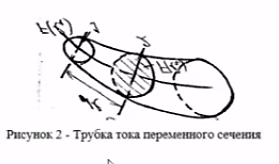
бобщение через потенциальную функцию:
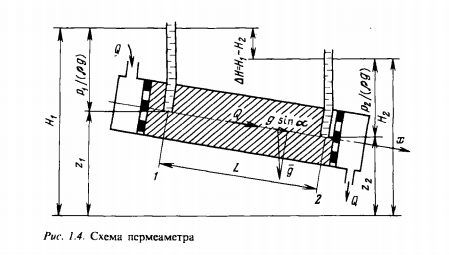
Трубка тока – элемент порового канала, по которому идет фильтрация. Пусть во всех сечениях нормальных к оси трубки тока площади сечения F меняются по длине. Нормальные к оси трубки тока сечения являются изобарические, т.е. давления равны. Из условия неразрывности фильтрационного потока следует, что массовый расход жидкости или газа через все изобарические сечения будет один и тот же.
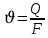
Чтобы перейти к массовым параметрам, нужно умножить левую и правую часть на плотность: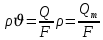
, Qm – массовый расход жидкости или газа.
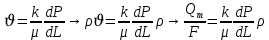
В общем случае k, μ, ρ зависят от давления, поэтому можно разделить переменные.
Введем понятия потенциальной функции (потенциал функции):
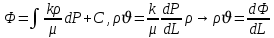
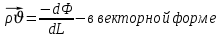
Введение потенциальной функции позволяет обобщить линейный закон фильтрации Дарси для случая фильтрации жидкости, газа, газированной жидкости, рассматривать их движение в упругих пластах и учитывать зависимости плотности, проницаемости, вязкости от давления.
Обобщенный закон гласит: массовая скорость фильтрации прямо пропорциональна градиенту потенциальной функции или градиенту потенциала скорости.
Движение флюида при справедливости потенциальной функции называют потенциальным движением.
Потенциальное движение газа или жидкости – движение, при котором массовая скорость фильтрации прямо пропорциональна градиенту потенциальной функции.
Обобщение при многофазном течении флюидов
Здесь играет роль:
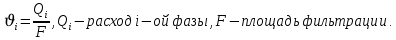
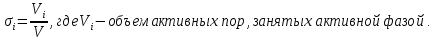
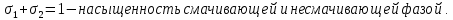
Экспериментально установлено, что для каждой фазы объемный расход Q возрастает с увеличением перепада давления и насыщенности данной фазой.
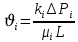
Введенные понятия можно обобщить на случай течения 3-х несмешивающихся флюидов.
Дифференциальные уравнения фильтрации жидкостей и газа в пористой среде
Задачи неустановившейся фильтрации жидкостей и газа в пористой среде решаются методами математической физики. Для этого составляются и решаются ДифУры. Обычно диф.уры. составляют по отношению к бесконечно малому элементу пористой среды и рассматривают изменение происходящие в этом элементе за бесконечно малый интервал времени.
В большинстве случаев эти дифуры составляются в частных производных. Решение их не всегда возможно, но и в этом случае они представляют интерес, так как из них можно получить безразмерные критерии подобия и найти сходства с другими изученными явлениями.
В подземной гидромеханике максимальное число неизвестных функций – 8.
Закон распределения скорости фильтрации:
Свойства добываемых флюидов:
Свойства пористой среды:
Частные случаи:
Изотермические процессы:
Фильтрация – очень медленный процесс, поэтому температурные изменения успевают компенсироваться с окружающей средой, т.е. окружающими г.п.
Аналитически решить систему уравнений очень сложно, поэтому приходится прибегать к использованию численных методов с помощью программных комплексов.
В систему уравнений для определения переменных параметров фильтрационного потока входят следующие уравнения:
Для решения этой системы уравнений задаются граничные условия (ГУ) на границе пласта и начальные условия (НУ) на начальный момент времени.
Совокупность перечисленных ДУ, а также ГУ и НУ (краевые условия) составляет задачу математической физики или краевую задачу подземной гидромеханики.
Уравнение неразрывности или сплошности фильтрационного потока
Выведем это уравнение для общего случая (для однородного сжимаемого флюида в деформируемой пористой среде):
Уравнение неразрывности выражает баланс массы сжимаемой жидкости в пределах постоянного элементарного объема, выделенного внутри пористой среды:
Внутри выделенного объема нет ни стоков, ни источников.
Источник – предельное положение нагнетательной скважины, радиус которой стремится к нулю.
Сток – предельное положение добывающей скважины, радиус которой стремится к нулю.
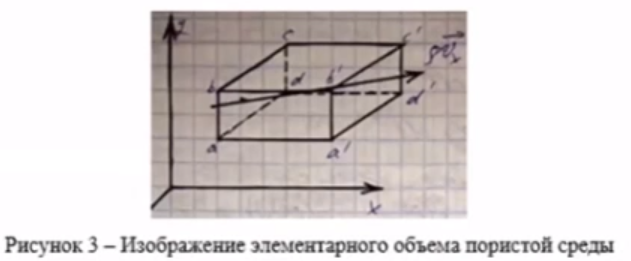
Объем параллелепипеда равен: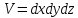
Рассмотрим движение вдоль оси OX:
Через грань ABCD втекают (за бесконечно малый интервал времени dt) следующая масса флюида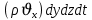
. Через грань A’B’C’D’ вдоль оси OX вытекает за время dt следующая масса жидкости:
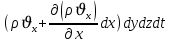
Изменение массы флюида за время dt за счет потока вдоль оси OX равно:
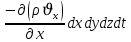
Рассуждая следующим аналогичным образом, рассматривая движения вдоль осей OY, OZ, можно записать такие же изменения вдоль других координатных осей:
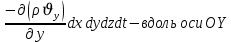
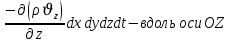
Учитывая выше сказанное, запишем общее изменение массы:
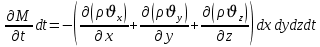
С другой стороны, масса флюида находится в поровом объеме dxdydzm.
Масса флюида, которая находится в поровом пространстве:
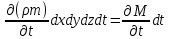
m, ρ – величины переменные
Поэтому общее изменение массы можно записать как:
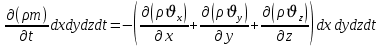
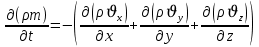
Получено уравнение неразрывности для общего случая – для неустановившейся фильтрации сжимаемой жидкости в деформируемом пласте.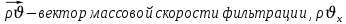
, 
, 
.
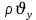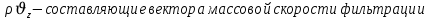Представим через дивергенцию векторного поля массовой скорости фильтрации (оператор Гамильтона):
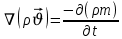
Уравнение неразрывности в укороченном виде.
Если фильтруются несжимаемая жидкость в недеформируемой пористой среде, то уравнение можно записать только через скорость:
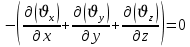
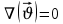
Для установившегося фильтрационного потока:
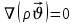
Для всех установившихся фильтрационных течений все уравнения будут приравниваться к нулю и носят название уравнение Лапласа.
Дифференциальные уравнения движения флюидов в пористой среде
Линейный закон фильтрации Дарси:
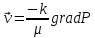
Последовав идее разложения фильтрационного потока на 3 составляющих вдоль координатных осей:
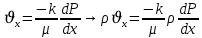
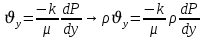
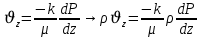
Введем потенциальную функцию течения или потенциал скорости:
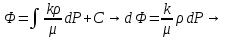
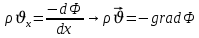
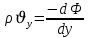
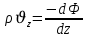
Используя введение потенциальной функции, запишем уравнение неразрывности и выразим его через потенциальную функцию:
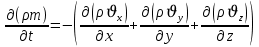
Верхняя граница наиболее полно изучена. Здесь отклонения, вызванные проявлением инерционных сил при увеличении скорости фильтрации.
Число Рейнольдса Re:
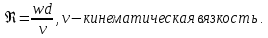
Попытки не увенчались успехом, у всех получилось свое критическое значение числа Рейнольдса.
Нелинейные законы фильтрации
-
Одночленная форма записи:
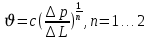
При n=2 получаем формула Краснопольского:
-
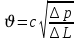
Двучленная форма записи:
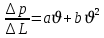
где, a и b – параметры, которые определяются экспериментально или по формулам справочных материалов. При малых скоростях:
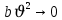
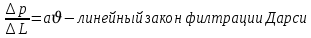
Вторя форма записи более физически обоснованная, потому что скорости фильтрации величины малые.
Обобщенный закон Дарси
-
Обобщение через потенциальную функцию -
Обобщение при многофазном течении флюидов
О
бобщение через потенциальную функцию:Трубка тока – элемент порового канала, по которому идет фильтрация. Пусть во всех сечениях нормальных к оси трубки тока площади сечения F меняются по длине. Нормальные к оси трубки тока сечения являются изобарические, т.е. давления равны. Из условия неразрывности фильтрационного потока следует, что массовый расход жидкости или газа через все изобарические сечения будет один и тот же.
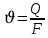
Чтобы перейти к массовым параметрам, нужно умножить левую и правую часть на плотность:
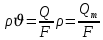, Qm – массовый расход жидкости или газа.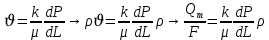 В общем случае k, μ, ρ зависят от давления, поэтому можно разделить переменные.
Введем понятия потенциальной функции (потенциал функции):
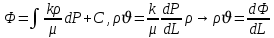
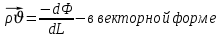
Введение потенциальной функции позволяет обобщить линейный закон фильтрации Дарси для случая фильтрации жидкости, газа, газированной жидкости, рассматривать их движение в упругих пластах и учитывать зависимости плотности, проницаемости, вязкости от давления.
Обобщенный закон гласит: массовая скорость фильтрации прямо пропорциональна градиенту потенциальной функции или градиенту потенциала скорости.
Движение флюида при справедливости потенциальной функции называют потенциальным движением.
Потенциальное движение газа или жидкости – движение, при котором массовая скорость фильтрации прямо пропорциональна градиенту потенциальной функции.
Обобщение при многофазном течении флюидов
Здесь играет роль:
-
Скорость фильтрации i-ой фазы
-
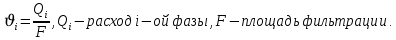
Насыщенность порового пространства i-ой фазой.
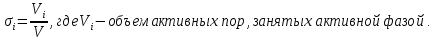
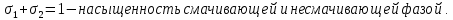
Экспериментально установлено, что для каждой фазы объемный расход Q возрастает с увеличением перепада давления и насыщенности данной фазой.
-
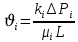
Относительная фазовая проницаемость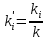
Введенные понятия можно обобщить на случай течения 3-х несмешивающихся флюидов.
Дифференциальные уравнения фильтрации жидкостей и газа в пористой среде
Задачи неустановившейся фильтрации жидкостей и газа в пористой среде решаются методами математической физики. Для этого составляются и решаются ДифУры. Обычно диф.уры. составляют по отношению к бесконечно малому элементу пористой среды и рассматривают изменение происходящие в этом элементе за бесконечно малый интервал времени.
В большинстве случаев эти дифуры составляются в частных производных. Решение их не всегда возможно, но и в этом случае они представляют интерес, так как из них можно получить безразмерные критерии подобия и найти сходства с другими изученными явлениями.
В подземной гидромеханике максимальное число неизвестных функций – 8.
-
P=P(x, y, z, t) – закон распределения давления в пласте
Закон распределения скорости фильтрации:
-
Vx= Vx(x, y, z, t) на ось OX -
Vy= Vy(x, y, z, t) на ось OY -
Vz= Vz(x, y, z, t) на ось OZ
Свойства добываемых флюидов:
-
Динамическая вязкость µ= µ(x, y, z, t) -
Плотность ρ=ρ(x, y, z, t)
Свойства пористой среды:
-
Коэф. пористости m=m(x, y, z, t) -
Коэф. проницаемость k=k(x, y, z, t)
Частные случаи:
-
Несжимаемая жидкость: µ=const, ρ=const. -
Недеформируемая пористая среды: k=const, m=const.
Изотермические процессы:
Фильтрация – очень медленный процесс, поэтому температурные изменения успевают компенсироваться с окружающей средой, т.е. окружающими г.п.
Аналитически решить систему уравнений очень сложно, поэтому приходится прибегать к использованию численных методов с помощью программных комплексов.
В систему уравнений для определения переменных параметров фильтрационного потока входят следующие уравнения:
-
Уравнение неразрывности или сплошности фильтрационного потока; -
Уравнения движения (в 3-х проекциях); -
Уравнения состояния пористой среды и флюидов.
Для решения этой системы уравнений задаются граничные условия (ГУ) на границе пласта и начальные условия (НУ) на начальный момент времени.
Совокупность перечисленных ДУ, а также ГУ и НУ (краевые условия) составляет задачу математической физики или краевую задачу подземной гидромеханики.
Уравнение неразрывности или сплошности фильтрационного потока
Выведем это уравнение для общего случая (для однородного сжимаемого флюида в деформируемой пористой среде):
Уравнение неразрывности выражает баланс массы сжимаемой жидкости в пределах постоянного элементарного объема, выделенного внутри пористой среды:
Внутри выделенного объема нет ни стоков, ни источников.
Источник – предельное положение нагнетательной скважины, радиус которой стремится к нулю.
Сток – предельное положение добывающей скважины, радиус которой стремится к нулю.
Объем параллелепипеда равен:
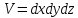
Рассмотрим движение вдоль оси OX:
Через грань ABCD втекают (за бесконечно малый интервал времени dt) следующая масса флюида
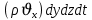. Через грань A’B’C’D’ вдоль оси OX вытекает за время dt следующая масса жидкости: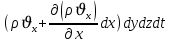 Изменение массы флюида за время dt за счет потока вдоль оси OX равно:
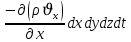
Рассуждая следующим аналогичным образом, рассматривая движения вдоль осей OY, OZ, можно записать такие же изменения вдоль других координатных осей:
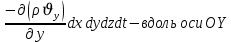
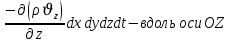
Учитывая выше сказанное, запишем общее изменение массы:
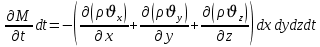
С другой стороны, масса флюида находится в поровом объеме dxdydzm.
Масса флюида, которая находится в поровом пространстве:
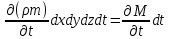
m, ρ – величины переменные
Поэтому общее изменение массы можно записать как:
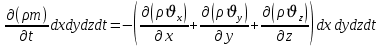
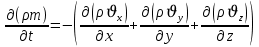
Получено уравнение неразрывности для общего случая – для неустановившейся фильтрации сжимаемой жидкости в деформируемом пласте.
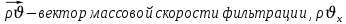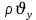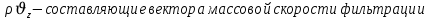, , .Представим через дивергенцию векторного поля массовой скорости фильтрации (оператор Гамильтона):
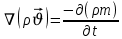
Уравнение неразрывности в укороченном виде.
Если фильтруются несжимаемая жидкость в недеформируемой пористой среде, то уравнение можно записать только через скорость:
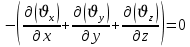
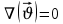
Для установившегося фильтрационного потока:
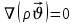
Для всех установившихся фильтрационных течений все уравнения будут приравниваться к нулю и носят название уравнение Лапласа.
Дифференциальные уравнения движения флюидов в пористой среде
Линейный закон фильтрации Дарси:
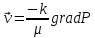
Последовав идее разложения фильтрационного потока на 3 составляющих вдоль координатных осей:
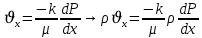
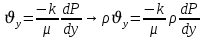
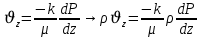
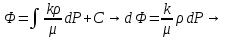
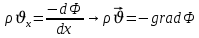
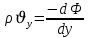
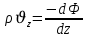
Введем потенциальную функцию течения или потенциал скорости: Используя введение потенциальной функции, запишем уравнение неразрывности и выразим его через потенциальную функцию: