Добавлен: 18.03.2024
Просмотров: 9
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Примеры задач по дисциплине
Для определения исходных данных используйте номер зачётной книжки (обязательно укажите его на титульном листе).
X, Y, Z – три последние цифры номера зачётной книжки, в том случае, когда X·Y·Z=0) подставлять в условие задачи X·Y·Z=1000.
Если X·Y=0 подставлять в условия задачи X·Y=100 (аналогично для X·Z, Y·Z, Z·X и других комбинаций.
Если Z = 0, подставлять в условие задачи Z=10 (также для X и Y).
Задача 1. Определить силу, действующую на фланец сосуда (рис. 1), находящегося под давлением 25 МПа. Внутренний диаметр прокладки D2=(100+ X·Y) мм.
| Рис. 1. Вариант крепления крышки сосуда: 1 – сосуд; 2 – прокладка; 3 – фланец сосуда (крышка); 4 – болт; 5 – шайба; 6 - гайка. |  |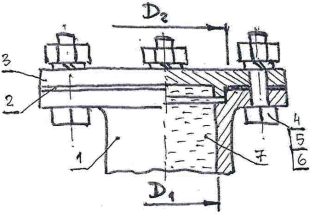
| Задача 2. Утяжелённая «бульба» ареометра (рис. 2) вытесняет 10 см3 жидкости, а прикреплённый к нему стержень, имеющий поперечное сечение 1,0 см2 погружается на глубину 10 см в воду, плотностью 1000 кг/м3. Определить глубину погружения ареометра в жидкость плотностью 1000·Z кг/м3. Рис. 2. |  |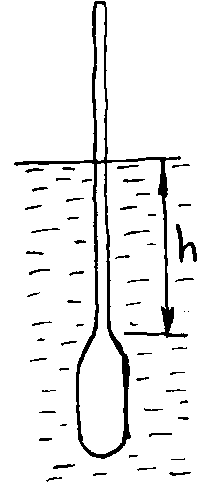
Задача 3. Напорная часть гидравлической системы механизма подъёма стрелы экскаватора (рис. 3) вмещает около 97 литров рабочей жидкости. В рабочей жидкости содержится несколько процентов нерастворённого воздуха. Определить, сколько рабочей жидкости нужно дополнительно подать из бака в напорную магистраль гидравлической системы для повышения давления в гидроцилиндрах стрелы на 15 МПа. Модуль объёмной упругости рабочей жидкости принять равным Ep=(10+Z)∙108 Н/м2.
| Рис. 3. Экскаватор: 1 – ковш; 2 – гидроцилиндр ковша; 3 – рукоять; 4 – гидроцилиндр рукояти; 5 – стрела; 6 – поворотная платформа; 7 – гусеничная тележка; 8 и 9 – гидроцилиндры стрелы. |  |
Задача 4. При каком давлении находится углекислый газ в баллоне огнетушителя ёмкостью 2 л, если после заполнения он имел массу (4,5+0,2∙Z) кг, а до заполнения 4,2 кг? Температура баллона 37 °С.
Задача 5. Записать процесс вывода уравнений равновесия элементарного объёма жидкости, неподвижной относительно сосуда, в котором она находится.
Задача 6. Определить коэффициент потери температуры трубопровода длиной (100+3·(X+Y+Z) км. Температура жидкости в начале трубопровода Т1=39 °С, в конце Т=20 °С, температура окружающей среды – 40 °С.
а
 б в |  |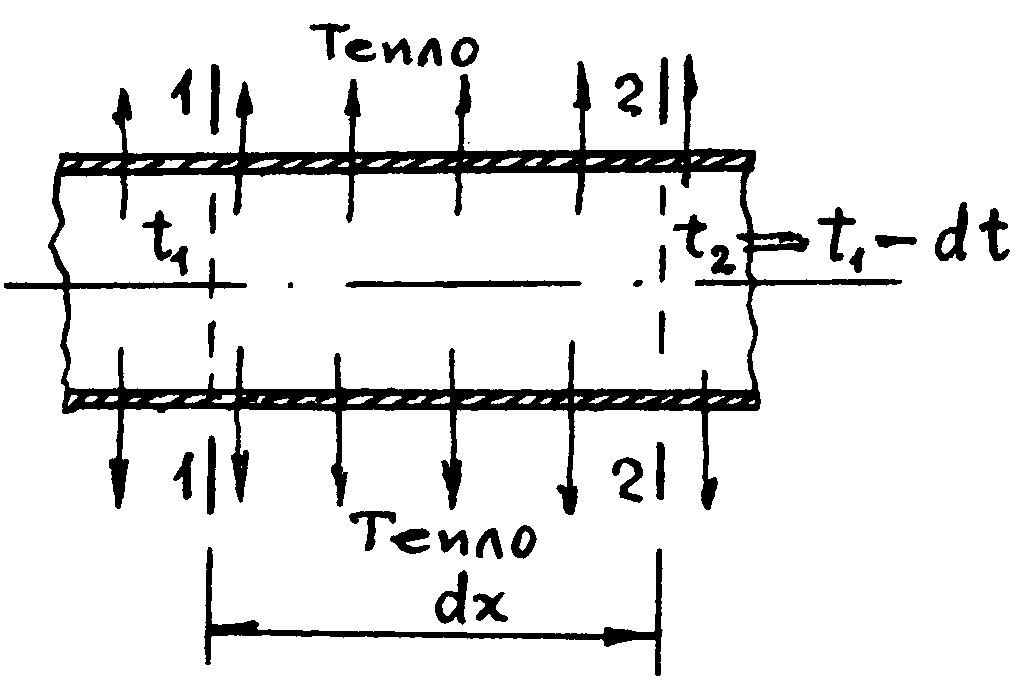
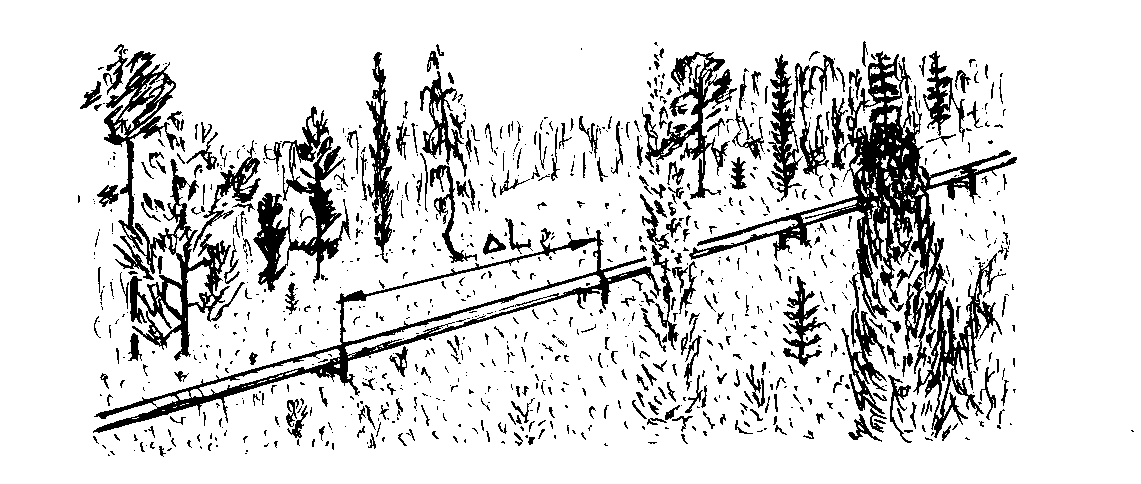
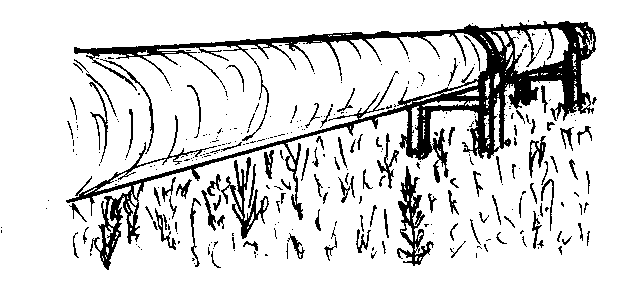
Рис. 4. Участок трубопровода (а), конструкция опоры трубопровода (б) и расчётная схема участка трубопровода (в): 1 – труба; 2 – опора; ΔL – расстояние между опорами.
Задача 7. Определить давление при гидравлическом ударе в трубопроводе (рис. 4) по данным из табл. 1.
Таблица 1
| Наименование исходных данных | Число X | |||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||
| Плотность жидкости, 103 кг/м3 | 00,8 | 00,9 | 81,0 | 81,1 | 81,2 | 81,3 | 00,8 | 00,9 | 81,0 | 81,1 | ||||
| Средняя скорость течения жидкости в трубе, м/с | 0,6 | 1,0 | 1,5 | 1,8 | 2,0 | |||||||||
| Внутренний диаметр трубы, мм | 80 | 90 | 100 | 125 | 150 | |||||||||
| Наружный диаметр трубы, мм | 88,5 | 101,3 | 114 | 140 | 165 | |||||||||
| Модуль упругости жидкости, 109 Па | 3 | 5 | 4 | 6 | 2 | |||||||||
Задача 8. Пожарный ствол (braindspuit, брандспойт) создает сплошную компактную струю воды (рис. 5). На выходе из ствола струя движется под углом
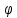к горизонту. Записать процесс составления уравнений движения струи в прямоугольной системе координат. Сопротивлением воздуха можно пренебречь.| Рис. 5. Пожарный с пожарным стволом: 1 – пожарный ствол; 2 - пожарный; 3 – струя; φ – угол струи к горизонту. |  |
Задача 9. Помещение длиной (100+10·Z) м, высотой 5 м и шириной (50+10·Z) м обогревается углём. Стены оштукатурены. Толщина слоя δ1 = 20 мм. Толщина стен δ2 = 0,51 м. Коэффициенты теплопроводности λ1 = 0,6 Вт/(м·К) и λ2 = 1,1 Вт/(м·К). Температура окружающей среды Тс2 = - 20 °С. Коэффициенты теплоотдачи: α1 = 8,7 Вт/(м2·К) и α2 = 23 Вт/(м2·К). Найти количество угля, которое нужно затратить в сутки, чтобы поддержать температуру среды Тс1 = + 15 °С внутри помещения. Тепловые потери через пол и потолок можно не учитывать.
-
Темы рефератов, дискуссий, блиц-опросов, эссе, сообщений при получении зачёта
Плотность жидкостей и газов. Для чего контролируют плотность жидкости при проведении технологических процессов?
Зависимость объёма жидкости от давления (сжимаемость жидкостей).
Зависимость объёма жидкости от температуры (температурное расширение жидкости). Как учитывается эта зависимость при проектировании машин и оборудования?
Сжимаемость газов (уравнение состояния газа).
Вязкость и реологические модели жидкостей. Для чего нужно контролировать реологические характеристики промывочной жидкости при проведении технологических процессов?
Принцип действия экспресс – анализаторов реологических характеристик жидкости (портативных вискозиметров).
Зависимость вязкости от температуры и давления.
Зависимость реологических характеристик жидкости от концентрации механических примесей и времени простоя механизма (формула А. Эйнштейна, статическое напряжение сдвига, СНС).
Закон Архимеда и примеры его использования в технике.
Закон Паскаля и пример его использования в технике.
Опасность технических жидкостей для здоровья человека и окружающей среды.
Уравнения равновесия жидкости и газа (уравнения Эйлера).
Пример использования уравнений Эйлера для жидкости, находящейся в баке движущейся машины.
Пример использования уравнений Эйлера для жидкости, находящейся во вращающейся ёмкости (в роторе центрифуги).
Движение тел в жидкости и газе (формула Н.Е. Жуковского для расчёта силы любого сопротивления тела, движущегося в жидкости или газе).
Элементы подземной гидравлики: фильтрация
Течение жидкости в круглой прямой трубе (течение Хагена – Пуазейля). Как это уравнение используется?
Течение охлаждающейся жидкости в трубе (течение В.Г. Шухова).
Уравнение Бернулли для жидкости, движущейся в трубе.
Число Рейнольдса и примеры его использования в гидравлических расчётах.
Гидравлический удар в трубах (уравнение Н.Е. Жуковского для гидроудара, течение Н.Е. Жуковского).
Теплопроводность: терминология, уравнение теплопроводности Фурье, тепловые потери через многослойную стенку.
Входной контроль по дисциплине
Перед изучением дисциплины желательно освежить знания по предшествующим дисциплинам физико-математического характера и выполнить нижеприведённые задания.
Запишите формулу закона Ньютона.
Запишите формулы для определения мощности механического привода при возвратно-поступательном и вращательном движениях, гидравлического и электрического приводов.
Запишите формулу, описывающую соударение двух тел.
Производные элементарных функций. Запишите производную функции
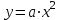
Интегрирование элементарных функций. Запишите значение интеграла функции
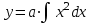
Полный дифференциал функции двух переменных.
Ряд Тейлора.
Дифференциальные уравнения.
Правила получения равнодействующей двух сил.
Работа силы
Запишите формулу для работы, затраченной на сжатие жидкости или газа.
Запишите формулу для работы, затраченной на сжатие твёрдого тела.
Запишите формулу для определения эквивалентного напряжения в стенке трубы (рис. 6), нагруженной внутренним давлением.
| Рис. 6. |  |  |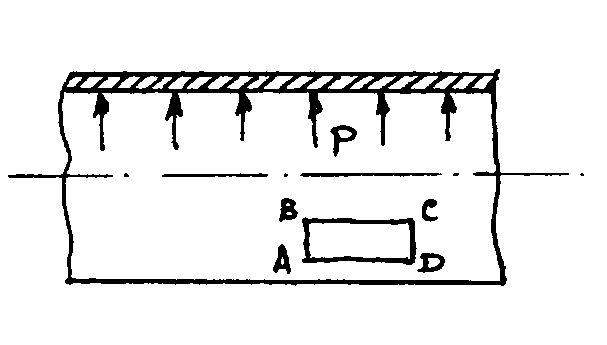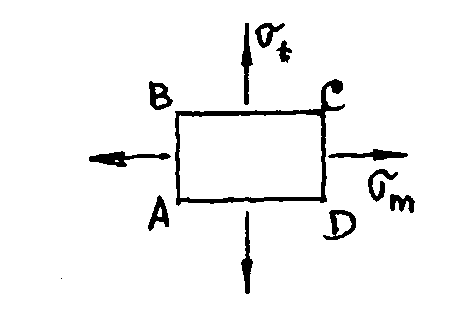
Методические рекомендации по текущему контролю
Текущий контроль успеваемости осуществляется в течение периода теоретического обучения по всем видам аудиторных занятий и самостоятельной работы студента в соответствии с утвержденным установленном порядке графиком учебного процесса.
К формам контроля текущей успеваемости по дисциплине относятся:
- проверка решенных задач.
- заслушивание и оценка ответов студента на вопросы, представленные в настоящем тексте.
Критерии прохождения студентами текущего контроля:
Текущая успеваемость студента оценивается положительно, если студент полностью выполнил практические работы и решил все задачи;
В противном случае текущая успеваемость студента оценивается отрицательно.
К основным формам текущего контроля относятся ответы на представленные вопросы и решенные задачи.
Результаты текущего контроля успеваемости учитываются преподавателем при проведении промежуточной аттестации. Отставание студента от графика текущего контроля успеваемости по изучаемой дисциплине приводит к образованию текущей задолженности.
Промежуточная аттестация осуществляется в конце семестра и завершает изучение дисциплины. Промежуточная аттестация помогает оценить более крупные совокупности знаний и умений.
Критерии оценивания:
«Зачтено» выставляется обучающемуся, если он способен изложить процесс получения основных уравнений механики жидкости и газа и использовать эти уравнения при проведении технических расчётов, самостоятельно решил 5 задач и может удовлетворительно отвечать на вопросы, представленные в настоящей программе и предназначенные для промежуточной аттестации.
Разработал _________________ П. М. Кондрашов