ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.03.2024
Просмотров: 21
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(ИС).
Вводится еще одна величина –
ИС/СИ ,где СИ - случайный индекс сгенерированный по шкале от 1 до 3 обратносимметричной матрицы (имеются соответствующие таблицы).
Таблица 1
Отношение ИС/СИ называется отношением согласованности (ОС). Значение ОС меньше или равное 0,1 будем считать приемлемым.
Используя приведенную схему расчета , получим для нашей матрицы ИС=0,13. СИ для нашей матрицы - 0,9. Получим ОС = 0,14, что не слишком хорошо.
Эти сравнения и вычисления устанавливают приоритеты элементов некоторого уровня иерархии относительно одного элемента следующего уровня. Если уровней больше, чем два, то различные векторы приоритетов могут быть объединены в матрицы приоритетов, из которых определяется один окончательный вектор приоритетов для нижнего уровня.
4. Пример иерархической композиции приоритетов. Задача о выборе школы.
Был проведен анализ трех школ A, B и С на предмет их желательности с точки зрения молодого человека. Для сравнения были выбраны шесть независимых характеристик: учеба, друзья, школьная жизнь, профессиональное обучение, подготовка к колледжу и обучение музыке.
Общая цель У Д Ш П К М
Силы
ау ад аш ск см
ап сп
ак вд вш вп вк сд сш
ам ву вм су
Сценарий
А В С
Для решения поставленной задачи необходимо выполнить следующие пункты:
Рассмотрим подробное решение поставленной задачи
1. Сравнение характеристик относительно общего удовлетворения школой (шкала 9 баллов)
Таблица 2.
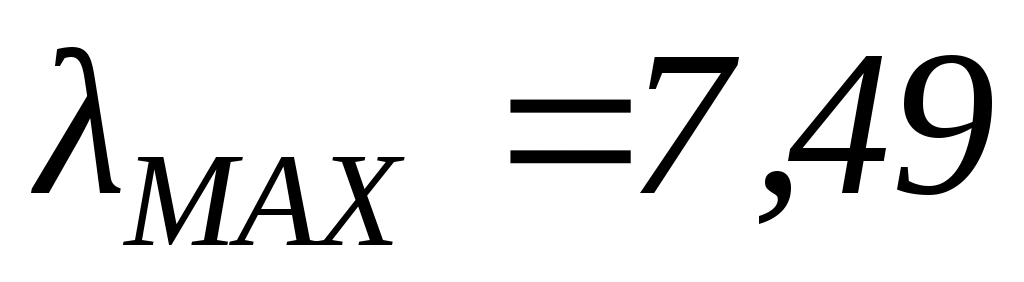
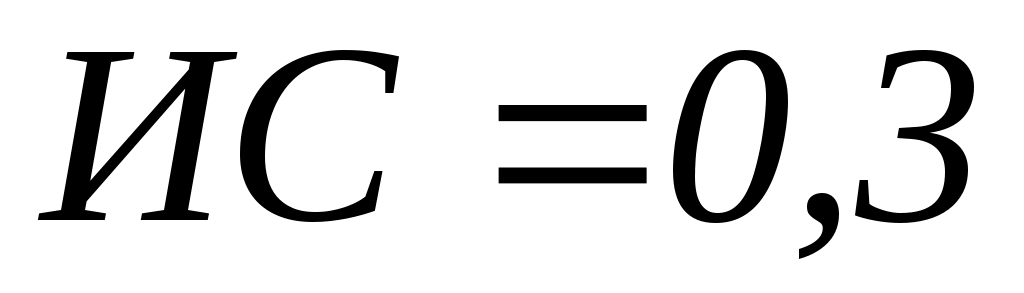
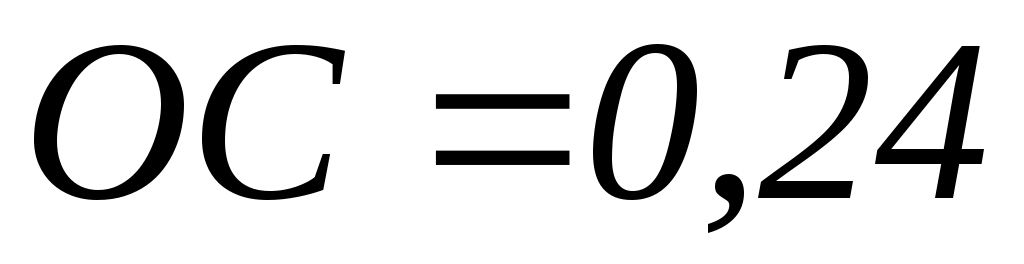
Вектор приоритетов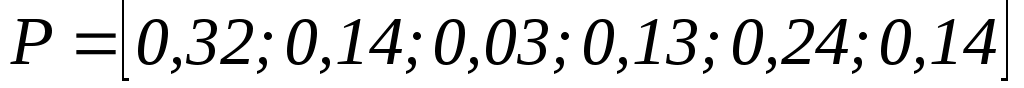
2. Таблицы 3-8
Для получения общей оценки каждой школы нужно умножить все оценки этой школы по некоторому критерию на вес этого критерия. Затем следует сложить значения, полученные для каждой школы, по всем критериям.
Математически - надо матрицу таблицы 17 умножить на вектор приоритетов таблицы 1, т.е.
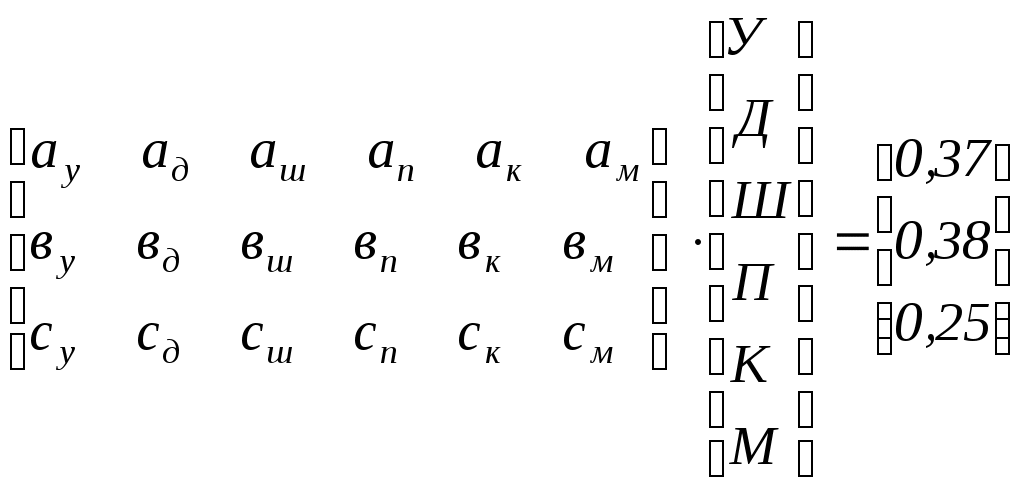- вектор приоритетов школ относительно цели – «большей удовлетворенности школой».
Была выбрана школа А, т.к. она получила почти такую же оценку, что и школа В и была бесплатной, а школа В была частной, за обучение в ней надо было платить 1600$ в год. Следует заметить однако, что решение было принято при значительной несовместимости суждений на уровне 2 (таблица 1), что могло привести к плачевному результату, но к счастью не привело. Через 3 года оценка была проведена вновь и были получены следующие приоритеты: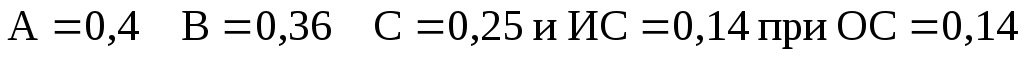
.
5. Оценка однородности иерархий
Рис. 3. Пример иерархии для оценки согласованности.
П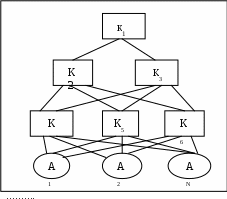
усть задана иерархия критериев и альтернатив
ИО1- индекс однородности ( согласованности ) 1-ого уровня;
{ИО2, ИО3}- вектор индексов однородности 2-ого уровня;
{ ИО4
, ИО5, ИО6}- вектор индексов однородности 3-его уровня;
W1- вектор приоритетов критериев K2 и K3 относительно K1;
{W2},{W3}- векторы приоритетов критериев K4, K5, K6 относительно K2 и K3
В этом случае ИОИ ,СИИ и ООИ можно определить по формулам:
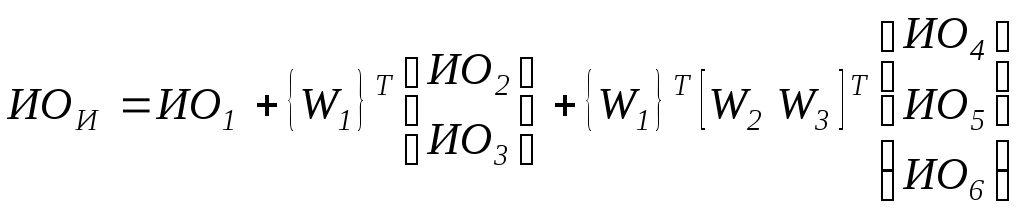
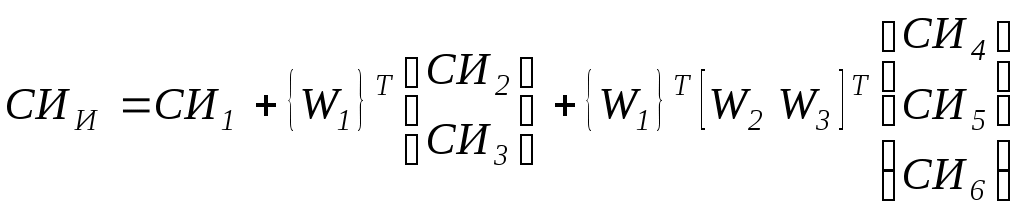
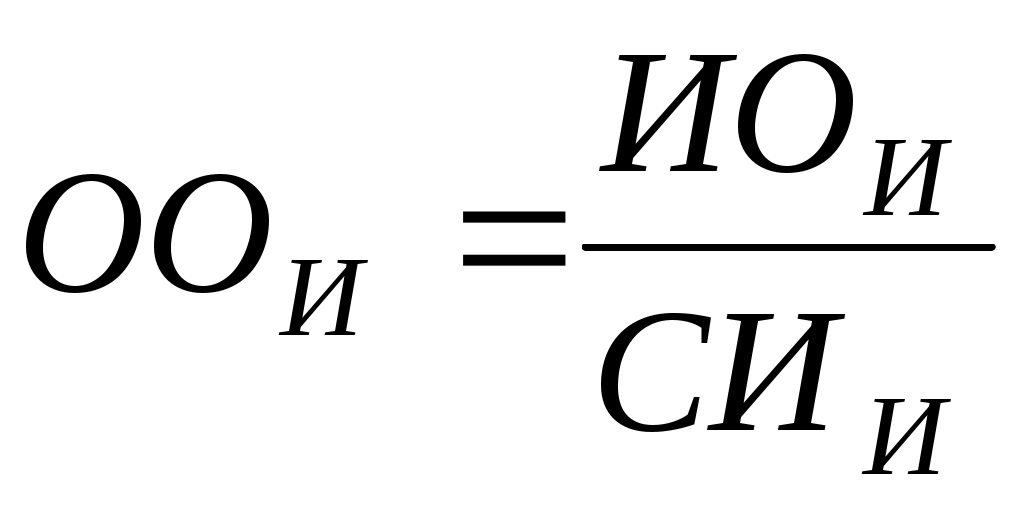
Однородность иерархии считается удовлетворительной при ООИ<0.1
6. Учет мнений нескольких экспертов
Для агрегирования мнений экспертов принимается среднегеометрическое, вычисляемое по следующему соотношению
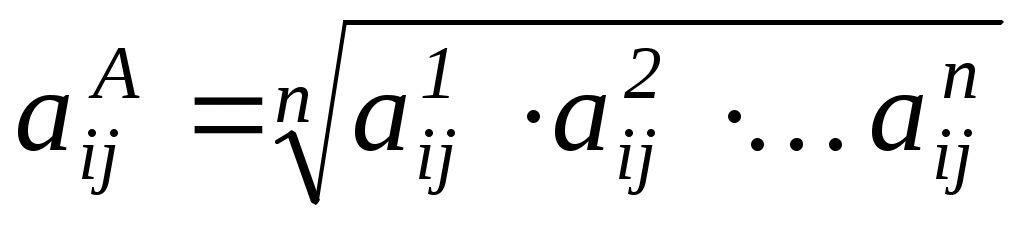
здесь -
агрегированная оценка элемента, принадлежащая i-ой строке и j-ому столбцу матрицы парных сравнений; n – число матриц парных сравнений, каждая из которых составлена одним экспертом.
Осреднение суждений экспертов может быть осуществлено и на уровне собственных векторов матриц парных сравнений. При этом результаты будут эквивалентны тем, которые получены после осреднения матрицы, если ОО<0.1 для матрицы.
В достаточно ответственных задачах, осреднение суждений экспертов производится с «весом». Сначала по следующей иерархии определяется их
«вес» (приоритет).
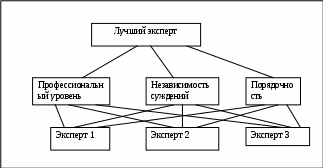
Рис. 4. Иерархия для нахождения «веса» экспертов.
Далее по формуле
,
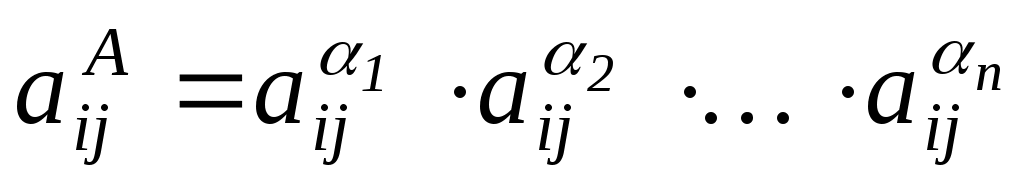где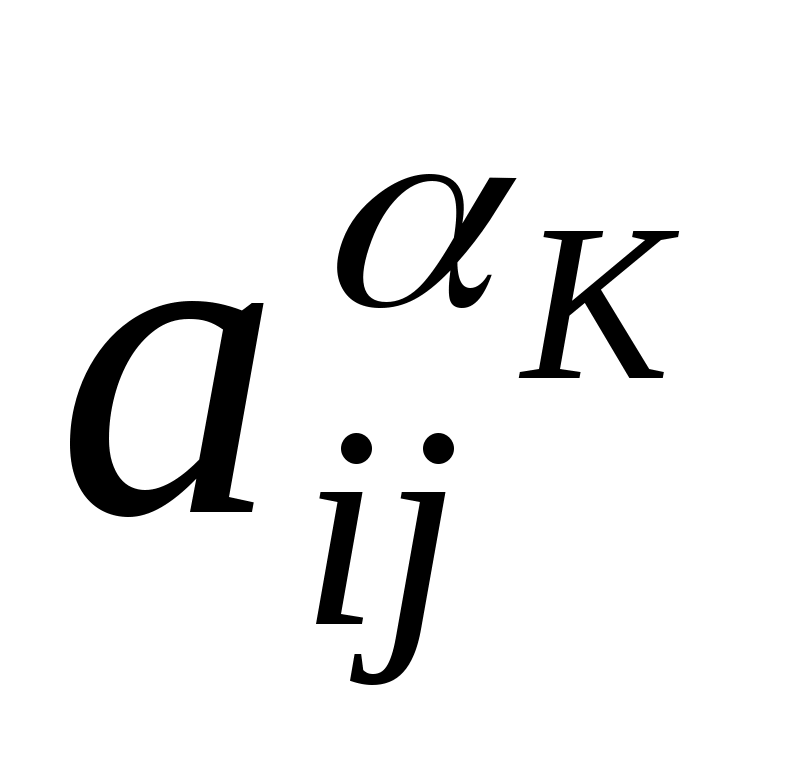
- оценка объекта, приведенная k-ым экспертом с весовым коэффициентом 
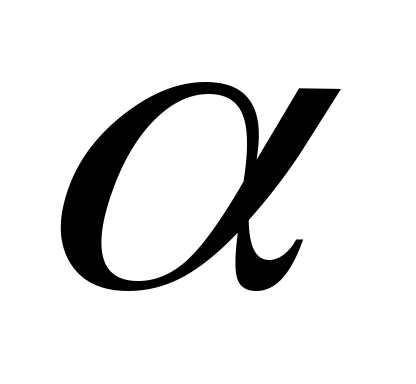при этом 
;
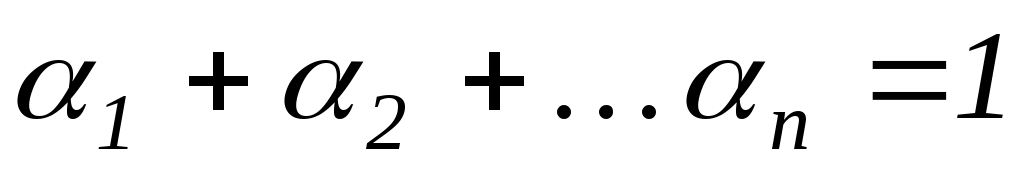определяют агрегированную матрицу попарных сравнений.
7. Выводы по МАИ
Подход к парным сравнениям, основанный на решении задачи о собственном значении, обеспечивает способ шкалирования, особенно в тех сферах, где не существует измерений и количественных сравнений. Мера согласованности позволяет возвратиться к суждениям, уточняя их для улучшения общей согласованности. Участие нескольких человек позволяет приходить к компромиссам между различными элементами, а также может вызвать диалог о том, каким следует быть действительному отношению - компромиссу между различными суждениями, представляющими разный опыт.
Этапы процесса проходят следующим образом:
При проведении попарных сравнений целей (критериев) обычно спрашивают, какая из них более важна, а при сравнении альтернатив (сценариев) – какая более предпочтительна или вероятна.
Задача
Правительственное агентство должно решить строить или не строить туннель и/или мост через реку, которую в настоящее время обслуживает паром.
Вводится еще одна величина –
ИС/СИ ,где СИ - случайный индекс сгенерированный по шкале от 1 до 3 обратносимметричной матрицы (имеются соответствующие таблицы).
Таблица 1
| Размерность матрицы | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| СИ | 0 | 0,58 | 0,9 | 1,12 | 1,24 | 1,32 | 1,41 | 1,45 | 1,49 | 1,51 | 1,48 | 1,56 | 1,57 | 1,59 |
Отношение ИС/СИ называется отношением согласованности (ОС). Значение ОС меньше или равное 0,1 будем считать приемлемым.
Используя приведенную схему расчета , получим для нашей матрицы ИС=0,13. СИ для нашей матрицы - 0,9. Получим ОС = 0,14, что не слишком хорошо.
Эти сравнения и вычисления устанавливают приоритеты элементов некоторого уровня иерархии относительно одного элемента следующего уровня. Если уровней больше, чем два, то различные векторы приоритетов могут быть объединены в матрицы приоритетов, из которых определяется один окончательный вектор приоритетов для нижнего уровня.
4. Пример иерархической композиции приоритетов. Задача о выборе школы.
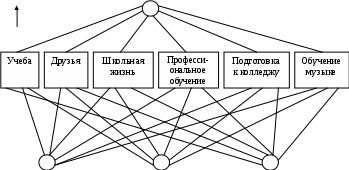
Был проведен анализ трех школ A, B и С на предмет их желательности с точки зрения молодого человека. Для сравнения были выбраны шесть независимых характеристик: учеба, друзья, школьная жизнь, профессиональное обучение, подготовка к колледжу и обучение музыке.
Удовлетворение школой
Общая цель У Д Ш П К М
Силы
ау ад аш ск см
ап сп
ак вд вш вп вк сд сш
ам ву вм су
Сценарий
А В С
Рис.2. Иерархия удовлетворения школой
Для решения поставленной задачи необходимо выполнить следующие пункты:
-
определить важность сил относительно общей цели -
определить действенность каждого сценария относительно сил -
определить приоритеты (т.е. действенность каждого сценария относительно цели).
Рассмотрим подробное решение поставленной задачи
1. Сравнение характеристик относительно общего удовлетворения школой (шкала 9 баллов)
Таблица 2.
| | Учеба | Друзья | Школьная жизнь | Проф. обучение | Подготовка к колледжу | Обучение музыке |
| Учеба | 1 | 4 | 3 | 1 | 3 | 4 |
| Друзья | 1/4 | 1 | 7 | 3 | 1/5 | 1 |
| Школьная жизнь | 1/3 | 1/7 | 1 | 1/5 | 1/5 | 1/6 |
| Проф. обучение | 1 | 1/3 | 5 | 1 | 1 | 1/3 |
| Подготовка к колледжу | 1/3 | 5 | 5 | 1 | 1 | 3 |
| Обучение музыке | 1/4 | 1 | 6 | 3 | 1/3 | 1 |
Вектор приоритетов
У Д Ш П К М
2. Таблицы 3-8
| 2) Таблица 3. | 3)Таблица 4. | 4)Таблица 5. | ||||||||||||||||||
| | Учеба | | Друзья | | Школьная жизнь | |||||||||||||||
| А | В | С | А | В | С | А | В | С | ||||||||||||
| А | 1 | 1/3 | 1/2 | А | 1 | 1 | 1 | А | 1 | 5 | 1 | |||||||||
| В | 3 | 1 | 3 | В | 1 | 1 | 1 | В | 1/5 | 1 | 1/5 | |||||||||
| С | 2 | 1/3 | 1 | С | 1 | 1 | 1 | С | 1 | 5 | 1 | |||||||||
      |       |    | ||||||||||||||||||
| 5)Таблица 6. | 6)Таблица 7. | 7)Таблица 8. | ||||||||||||||||||
| | Проф. обучение | | Подготовка к колледжу | | Обучение музыке | |||||||||||||||
| А | В | С | А | В | С | А | В | С | ||||||||||||
| А | 1 | 9 | 7 | А | 1 | 1/2 | 1 | А | 1 | 6 | 4 | |||||||||
| В | 1/9 | 1 | 1/5 | В | 2 | 1 | 2 | В | 1/6 | 1 | 1/3 | |||||||||
| С | 1/7 | 5 | 1 | С | 1 | 1/2 | 1 | С | 1/4 | 3 | 1 | |||||||||
   | | | ||||||||||||||||||
-
Итоговая таблица приоритетов школ для сил. Таблица 9.
| | Учеба | Друзья | Школьная жизнь | Проф. обучение | Подготовка к колледжу | Обучение музыке |
| А | 0,16 | 0,33 | 0,45 | 0,77 | 0,25 | 0,69 |
| В | 0,59 | 0,33 | 0,09 | 0,05 | 0,50 | 0,09 |
| С | 0,25 | 0,33 | 0,46 | 0,17 | 0,25 | 0,22 |
-
Общая оценка школы относительно целей
Для получения общей оценки каждой школы нужно умножить все оценки этой школы по некоторому критерию на вес этого критерия. Затем следует сложить значения, полученные для каждой школы, по всем критериям.
Математически - надо матрицу таблицы 17 умножить на вектор приоритетов таблицы 1, т.е.
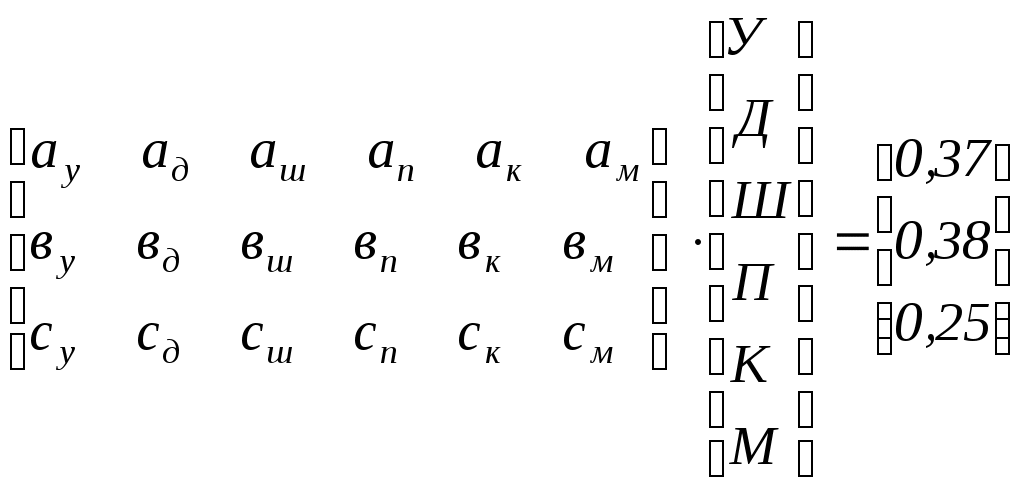- вектор приоритетов школ относительно цели – «большей удовлетворенности школой».Была выбрана школа А, т.к. она получила почти такую же оценку, что и школа В и была бесплатной, а школа В была частной, за обучение в ней надо было платить 1600$ в год. Следует заметить однако, что решение было принято при значительной несовместимости суждений на уровне 2 (таблица 1), что могло привести к плачевному результату, но к счастью не привело. Через 3 года оценка была проведена вновь и были получены следующие приоритеты:
.5. Оценка однородности иерархий
Рис. 3. Пример иерархии для оценки согласованности.
П
усть задана иерархия критериев и альтернатив
ИО1- индекс однородности ( согласованности ) 1-ого уровня;
{ИО2, ИО3}- вектор индексов однородности 2-ого уровня;
{ ИО4
, ИО5, ИО6}- вектор индексов однородности 3-его уровня;
W1- вектор приоритетов критериев K2 и K3 относительно K1;
{W2},{W3}- векторы приоритетов критериев K4, K5, K6 относительно K2 и K3
В этом случае ИОИ ,СИИ и ООИ можно определить по формулам:
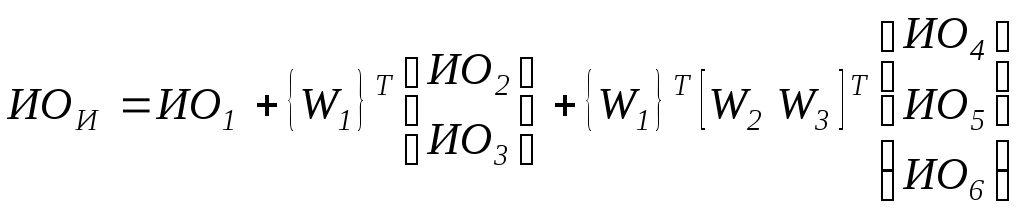
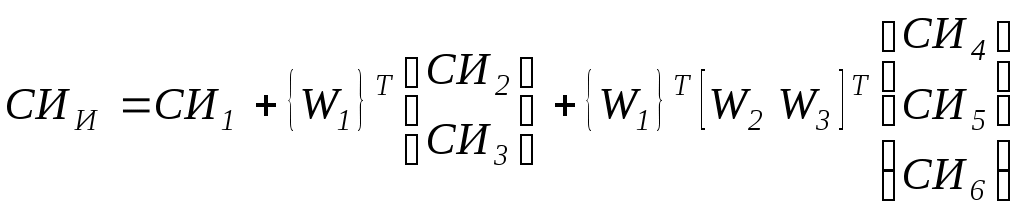
Однородность иерархии считается удовлетворительной при ООИ<0.1
6. Учет мнений нескольких экспертов
Для агрегирования мнений экспертов принимается среднегеометрическое, вычисляемое по следующему соотношению
здесь -
агрегированная оценка элемента, принадлежащая i-ой строке и j-ому столбцу матрицы парных сравнений; n – число матриц парных сравнений, каждая из которых составлена одним экспертом.Осреднение суждений экспертов может быть осуществлено и на уровне собственных векторов матриц парных сравнений. При этом результаты будут эквивалентны тем, которые получены после осреднения матрицы, если ОО<0.1 для матрицы.
В достаточно ответственных задачах, осреднение суждений экспертов производится с «весом». Сначала по следующей иерархии определяется их
«вес» (приоритет).
Рис. 4. Иерархия для нахождения «веса» экспертов.
Далее по формуле
,где
- оценка объекта, приведенная k-ым экспертом с весовым коэффициентом при этом ;определяют агрегированную матрицу попарных сравнений.
7. Выводы по МАИ
Подход к парным сравнениям, основанный на решении задачи о собственном значении, обеспечивает способ шкалирования, особенно в тех сферах, где не существует измерений и количественных сравнений. Мера согласованности позволяет возвратиться к суждениям, уточняя их для улучшения общей согласованности. Участие нескольких человек позволяет приходить к компромиссам между различными элементами, а также может вызвать диалог о том, каким следует быть действительному отношению - компромиссу между различными суждениями, представляющими разный опыт.
Этапы процесса проходят следующим образом:
-
Сформулируйте задачу. -
Поставьте задачу в общем плане - вставьте ее (если есть необходимость) в большую систему, включающую другие действующие лица, их цели и результаты. -
Идентифицируйте критерии, влияющие на задачу. -
Постройте иерархию общих критериев, частных критериев, свойств альтернатив и самих альтернатив. -
В задаче со многими участниками уровни могут относиться к окружающей среде, акторам, их целям, политике и результатам, из которых получаем обобщенный результат (состояние сферы действия). -
Чтобы устранить неясность, тщательно определите каждый элемент в иерархии. -
Установите приоритеты первичных критериев относительно их воздействия на общую цель, называемую фокусом. -
Ясно сформулируйте вопрос для парных сравнений в каждой матрице. Обратите внимание на ориентацию каждого вопроса, например, стоимость должна уменьшаться, а эффективность увеличиваться.
При проведении попарных сравнений целей (критериев) обычно спрашивают, какая из них более важна, а при сравнении альтернатив (сценариев) – какая более предпочтительна или вероятна.
-
Установите приоритеты частных критериев относительно своих общих критериев. -
Введите суждения о попарных сравнениях и их обратные величины. -
Вычислите приоритеты путем, например, суммирования элементов каждого столбца и деления каждого элемента на общую сумму столбца. Усредните по строкам результирующую матрицу, и вы получите вектор приоритетов. -
В случае сценариев прокалибруйте их переменные состояния по шкале от -8 до +8 в зависимости от того, насколько они отличаются от существующего состояния, обозначаемого 0. -
Составьте веса в иерархии для получения общих приоритетов, а также составных значений переменных состояния, которые вместе определяют общий результат. -
В случае выбора среди альтернатив выберите альтернативу с небольшим приоритетом. -
В случае размещения ресурсов оцените стоимость альтернативы, вычислите отношение эффективности к стоимости и распределите ресурсы соответствующим образом: или полностью, или пропорционально. В задаче определения приоритетов стоимости распределите ресурсы пропорционально приоритетам.
Задача
Правительственное агентство должно решить строить или не строить туннель и/или мост через реку, которую в настоящее время обслуживает паром.