ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.03.2024
Просмотров: 10
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Муниципальное бюджетное образовательное учреждение
«Лицей №122» города Барнаула
Индивидуальный итоговый проект
«Числа Фибоначчи и Золотое сечение»
Выполнил:
Грибанов Михаил ,
ученик 9Б класса
Руководитель проекта:
Королёва В.И,
учитель математики
Барнаул 2023
Оглавление
1. Введение (цель, задачи, гипотеза, методы исследования)............3
2.История появления………………..4
3. Теоретическая часть............................................................5
4.А какова связь между ЗС и числами Фибоначчи?........
5. Заключение.....................................................................14
Введение
Человек стремится к знаниям, пытается изучить мир, который его
окружает. В процессе наблюдений появляются многочисленные вопросы, на которые, соответственно требуется найти ответы. Человек ищет эти ответы, а находя их, появляются другие вопросы. Сегодня, в век высоких технологий, изучение ведётся не только на нашей планете Земля, но и за её пределами – во Вселенной. Но это не значит, что на Земле всё изучено, а наоборот, остаётся огромное количество непонятных и необъяснимых явлений. Но есть «ответы», которые дают объяснение сразу нескольким таким явлениям. Оказывается, закономерность явлений природы, строение и многообразие живых организмов на нашей планете, всё, что нас окружает, поражая воображение своей гармонией и упорядоченностью, законы мироздания, движение человеческой мысли и достижения науки – всё это можно объяснить последовательностью Фибоначчи.
Последовательность Фибоначчи все медленнее и медленнее стpемится к некоторому постоянному иppациональному соотношению – числу с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно. Числа Фибоначчи встречаются и в жизни. Существует мнение, что почти все утверждения, находящие числа Фибоначчи в природных и исторических явлениях, неверны — это распространённый миф, который часто оказывается неточной подгонкой под желаемый результат. В мире очень много примеров применения этих чисел в строительстве людей, а также в природе.
Числа Фибоначчи (строка Фибоначчи) — числовая последовательность, первые два числа которой являются 0 и 1, а каждое последующее за ними число является суммой двух предыдущих. Представляет собой частный пример линейной рекуррентной последовательности (рекурсии).
Заблуждения, связанные с числами Фибоначчи
Благодаря современной поп-культуре с этой числовой последовательностью связано множество популярных мифов:
Универсальность. Во многих источниках числа Фибоначчи и золотая спираль позиционируются как универсальный закон мироздания, с помощью которого можно описать любой природный процесс или объекты, от расположения лепестков цветка до формы спиральных галактик. Хотя в отношении многих природных явлений это действительно так, принцип не является всеобъемлющим: например, те же рукава спиральных галактик или раковина моллюска наутилуса закручены по логарифмической спирали, которая, хоть и близка по форме к золотой, все же ей не является.
Идеальность. Распространено мнение, что золотое сечение и спираль Фибоначчи описывают идеальные пропорции. Однако исследования показали, что объекты, построенные по этому принципу (например человеческое тело), при демонстрации обычным людям воспринимаются обычно как диспропорциональные, вытянутые. Отсюда является заблуждением и утверждение, что все великие художники эпохи Возрождения и последующих времен использовали принцип золотой спирали в своих работах. Такие эксперименты действительно случались, но это не было распространенным явлением.
Практическая применимость. Еще один миф говорит о том, что использование золотого сечения и чисел Фибоначчи в любом сфере деятельности дает положительный результат. Но, например, криптографы знают, что метод Фибоначчи с запозданием не является идеальным способом усилить шифрование — многие генераторы случайных чисел на его основе либо медленно работают, либо имеют недостаточный порог устойчивости к взлому. А использование принципов золотого сечения в архитектуре или промышленном дизайне редко сочетается с оптимизацией производства.
Актуальности этой темы уделяют недостаточно внимания. На примере чисел Фибоначчи можно показать насколько они могут быть глобальны и широко применимы не только в математике, но и в повседневной жизни. Так как они встречаются нам в различных творениях природы. Знания о них будут полезны во многих науках. Числа Фибоначчи и их различные инварианты отражаются во всех творениях мироздания, которые продуманы и подчинены единым законам природы и имеют большой практический и теоретический интерес во многих науках.
Цель данной работы: изучить проявление чисел Фибоначчи и связанного с ними закона золотого сечения в строении живых и неживых объектов, найти примеры использования чисел Фибоначчи, а также связь с золотым сечением
Задачи:
1.Изучить историю создания чисел Фибоначчи
2. Изучить свойства чисел Фибоначчи
3.Изучить золотое сечение
5.Изучить практическое применение чисел Фибоначчи
6.Изучить связь чисел Фибоначчи с золотым сечением
Объект исследования – область применения чисел Фибоначчи; свойства чисел Фибоначчи.
Проблема, которую призвано разрешить наше исследование, заключается в том, что мы не знаем и не видим в окружающей нас жизни числовые закономерности, которые укладываются в ряд Фибоначчи.
Изучение этих чисел не предусмотрено уроками математики, поэтому чтобы познакомится с ними подробнее, необходимо использовать разнообразные источники информации: дополнительную литературу по предмету и интернет ресурсы.
Методы исследования в работе:
• теоретический (логическая ступень познания).
• эмпирический (наблюдение, эксперимент, измерение).
• сравнение.
• классификация.
• математическое моделирование
историю создания чисел Фибоначчи
Леонардо Пизанский — итальянский купец из Пизы, первый крупный математик средневековой Европы. Наиболее известен под прозвищем Фибоначчи.
Отец Фибоначчи по торговым делам часто бывал в Алжире, и Леонардо изучал там математику у арабских учителей. Позже Фибоначчи посетил Египет, Сирию, Византию, Сицилию. Он ознакомился с достижениями античных и индийских математиков в арабском переводе. На основе усвоенных им знаний Фибоначчи написал ряд математических трактатов, представляющих собой выдающееся явление средневековой западноевропейской науки.
Фибоначчи написал несколько математических сочинений. Наиболее известным из них является "Liberabaci". Сочинение представляло своеобразную математическую энциклопедию эпохи средневековья. Особенный интерес представляет раздел, в котором Фибоначчи сформулировал и решил ряд математических задач, представляющих интерес с точки зрения общих перспектив развития математики. Наиболее известной из сформулированных Фибоначчи задач является "задача о размножении кроликов", которая привела к открытию числовой последовательности
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 и т.д.
Также ученый привел ряд закономерностей: Любое число из ряда, разделенное на последующее, будет равно значению, которое стремится к 0,618. Причем первые числа Фибоначчи не дают такого числа, но по мере продвижения от начала последовательности это соотношение будет все более точным.
Если же поделить число из ряда на предыдущее, то результат устремится к 1,618.
Одно число, поделенное на следующее через одно, покажет значение, стремящееся к 0,382.
свойства чисел Фибоначчи
Числа Фибоначчи имеют удивительные свойства:
Каждое третье число четно;
каждое четвертое число кратно 3;
каждое пятнадцатое число оканчивается нулем;
Если какой-либо член последовательности Фибоначчи разделить на предшествующий ему (например, 13:8), получится 1.61
Золотое сечение
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.).
Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением, как в геометрии, так и в искусстве, особенно в архитектуре. Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, величайшего математика Италии и Леонардо оставил свою затею. Он прекрасно понимал значение науки для искусства. В 1496 г. по приглашению герцога Моро Лука Пачоли приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как
выражение божественного триединства бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок - бога отца, а весь отрезок - бога духа святого).
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Именно Леонардо да Винчи дал золотому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.
Теоретическая часть
Золотое сечение - соотношение двух величин b и a, a > b, когда справедливо a/b = (a+b)/a. Число, равное отношению a/b, обычно обозначается прописной греческой буквой
Φ {\displaystyle \Phi }. Из исходного равенства нетрудно получить, что число
Обратное число
Отсюда следует, что
.Для практических целей ограничиваются приблизительным значением
= 1,618. В процентном округлённом значении золотое сечение — это деление какой-либо величины в отношении 62 % и 38 %.Исторически изначально золотым сечением именовалось деление отрезка АВ точкой С на две части (меньший отрезок АС и больший отрезок ВС), чтобы для длин отрезков было верно AC/BC = BC/AВ.
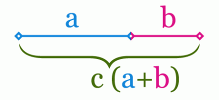
Число
Φ {\displaystyle \Phi } называется также золотым числом. Если мы примем весь отрезок c за 1, то отрезок a будет равен 0,618, отрезок b - 0,382. Применение связи и закономерностей золотого сечения, числа Фибоначчи (0,618) можно найти не только в математике, но и в природе, в истории, в архитектуре и строительстве и во многих других науках. Также можно рассчитать высоту двери, окон, креста. И везде будет просматриваться принцип золотого сечения.