Автономная некоммерческая образовательная организация высшего образования «Сибирский институт бизнеса и информационных технологий»

Письменная работа

По дисциплине: «Высшая математика»

На тему: «Элементы комбинаторного анализа»

Выполнил:студент группы ЭН-1421(2)

Ф.И.О. Николаева Алена Игоревна

Омск 2023

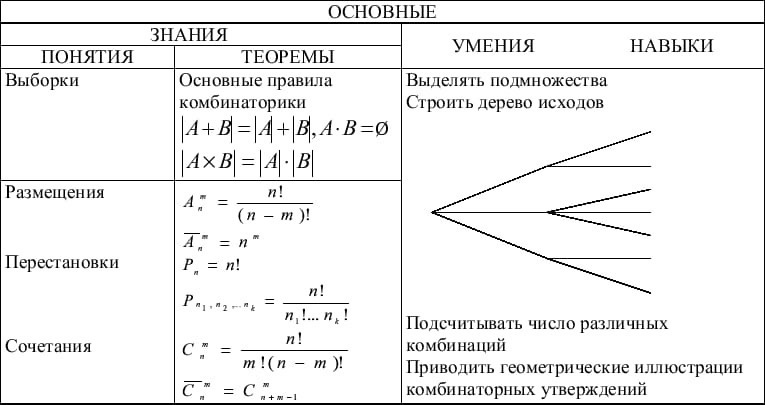
Задание 1

												6
			9
				10
								11
4														8
			2
									3
						5
1
			12
		7
																14
								13
								15

---

6 В

9 Р

А

З

М

Е

Щ

Е

Н

И

Е

М

Р

10П

Е

Р

Е

С

Т

А

Н

О

В

К

О

Й

Я

11 С

О

Ч

Е

Т

А

Н

И

Е

М

Н

4 С

О

8 И

Т

2 Л

С

Н

Р

Е

3 П

Т

Ф

У

Й

5 Р

Е

Н

И

1 К

О

М

Б

И

Н

А

Т

О

Р

И

К

А

Н

Т

Н

М

Е

Я

И

У

И

С

Ч

Т

Р

Ц

Е

И

А

Н

Я

С

Р

А

12 К

Л

Н

Я

7 Т

О

П

О

Л

О

Г

И

Ч

Е

С

К

А

Я

М

Т

Я

14 Д

П

Е

И

О

Л

С

З

Ь

К

И

Н

Р

Ц

13Р

А

З

Б

И

Е

Н

И

Е

М

И

Я

Т

Е

НX 15К И Т А Й С К О Й

Й

О

15К

И

Т

А

Й

С

К

О

Й

---

---

По горизонтали:
1.Раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка)?

7.Это молодая область математики, возникшая в последней четверти 20-го века, которая занимается следующими вопросами:

1) Применение методов топологии к задачам дискретной математики;

2) Топологические обобщения задач дискретной геометрии;

3) Дискретизация топологических понятий.

9.________ из n элементов по k называется упорядоченный набор из k различных элементов некоторого n-элементного множества.

10. ______ из n элементов (например чисел 1, 2, … n) называется всякий упорядоченный набор из этих элементов. Перестановка также является размещением из n элементов по n.

11. ______ из n по k называется набор k элементов, выбранных из данных n элементов.

13. _____ числа n называется всякое представление n в виде неупорядоченной суммы целых положительных чисел.

15.В книге какой страны можно заметить в символике «Книги Перемен» Комбинаторные мотивы?

По вертикали:

2. Кто ввел Термин «комбинаторика»?

3. Рассматривает задачи о перечислении или подсчёте количества различных конфигураций (например, перестановок) образуемых элементами конечных множеств?

4. К данному разделу относятся некоторые вопросы теории графов, а также теории матроидов.

5. Эта Теория изучающает условия, при которых в произвольно формируемых математических объектах обязан появиться некоторый порядок. Что за теория?

6. Этот раздел отвечает на вопросы вида: какова вероятность присутствия определённого свойства у заданного множества?

8. Применение идей и методов комбинаторики к бесконечным (в том числе, несчётным) множествам?

12. _____ числа n называется всякое представление n в виде упорядоченной суммы целых положительных чисел.

14. Иногда под комбинаторикой понимают более обширный раздел _____ математики.

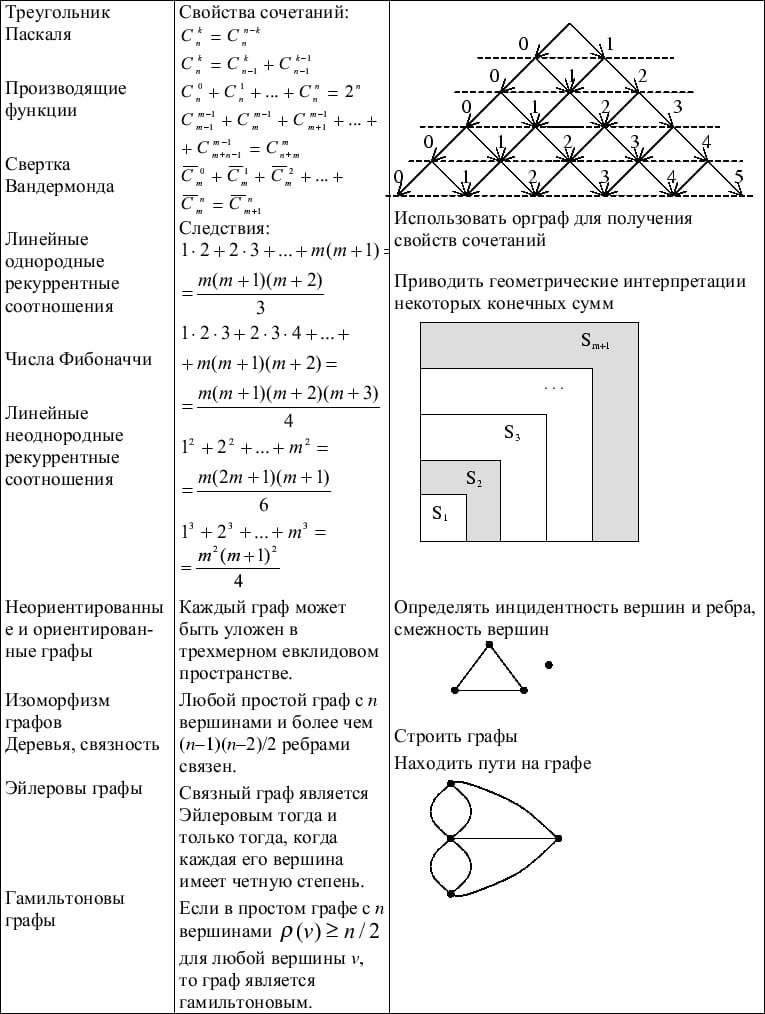
Задание 2

Вопросы	Формулы
A Это любое подмножество из m - элементов, которые принадлежат множеству, состоящему из n - различных элементов. (Порядок не важен).	1
B Это любое упорядоченное подмножество m из элементов множества n. (Порядок важен).	2
C Если m = n, то эти размещения называются перестановками.	3
D Число сочетаний из n, элементов по n-m равно число сочетаний из n элементов по m	4
	5
	6

---

Ответ: A5, B1, C6, D3.

Задание 3

---

Смотрите также файлы

• Инистерство науки и высшего образования российской федерации.docx

• Отчет учителя начальных классов моу Чучковская средняя школа.docx

• Курсовая работа по теме Ревматоидный артрит. Планирование реабилитации.docx

• 11. Особенности восприятия и освоения пространственных отношений детьми дошкольного возраста.docx

• Кркем ебек пні бойынша кнтізбеліктаырыпты жоспарлау.docx