Файл: Приведена выборка 60 результатов измерений случайной величины Х.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.03.2024
Просмотров: 19
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Приведена выборка 60 результатов измерений случайной величины Х
| 93,5 | 62 | 74,3 | 54,3 | 55 | 65,8 | 53,9 | 63,5 | 75 | 53 | 63,8 | 49,2 |
| 73,3 | 72,5 | 64,3 | 54,6 | 72,9 | 30,9 | 44,7 | 60,7 | 53,4 | 58,8 | 56,9 | 64,6 |
| 31,6 | 73,7 | 84,4 | 63,8 | 74 | 80,5 | 64,4 | 34,6 | 54,1 | 62,1 | 61,7 | 92,5 |
| 73,9 | 53,5 | 63,7 | 74,3 | 52,8 | 64,6 | 73,8 | 51,8 | 62,5 | 42,3 | 34,7 | 64,1 |
| 52,4 | 64,8 | 73,9 | 41,4 | 52,4 | 72,4 | 62,9 | 64,1 | 57,7 | 50,8 | 64 | 62,7 |
-
Построить интервальный вариационный ряд (ряд 1) по частотам, относительным частотам и накопленным частотам. -
От ряда 1 перейти к точечному вариационному ряду (ряд 2).
Определим максимальное и минимальное значения во всей выборке
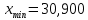
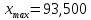
Количество интервалов определим по формуле Стерджеса
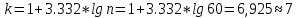
а длина интервала будет равна:
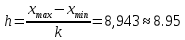
Получим следующие интервалы и входящие в них значения
| (30,9; 39,85) | 30,9; 31,6; 34,6; 34,7 |
| (39,85; 48,8) | 41,4; 42,3; 44,7 |
| (48,8; 57,75) | 49,2; 50,8; 51,8; 52,4; 52,4; 52,8; 53; 53,4; 53,5; 53,9; 54,1; 54,3; 54,6; 55; 56,9; 57,7 |
| (57,75; 66,7) | 58,8; 60,7; 61,7; 62; 62,1; 62,5; 62,7; 62,9; 63,5; 63,7; 63,8; 63,8; 64; 64,1; 64,1; 64,3; 64,4; 64,6; 64,6; 64,8; 65,8 |
| (66,7; 75,65) | 72,4; 72,5; 72,9; 73,3; 73,7; 73,8; 73,9; 73,9; 74; 74,3; 74,3; 75 |
| (75,65; 84,6) | 80,5; 84,4 |
| (84,6; 93,55) | 92,5; 93,5 |
Посчитаем частоты на каждом интервале (количество значений входящих в интервал), относительные частоты (частости; отношение частоты к общему количеству) и накопленные частоты, которые получаются суммированием частот значений, предшествующих данному. Также сразу найдем средние значеинй каждого интервала и получим сразу интервальный вариационный и точечный ряды.
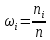
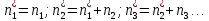
| Интервалы | 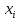 | 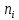 | 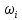 | 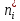 | |
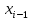 | 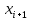 | ||||
| 30,900 | 39,850 | 35,375 | 4 | 0,067 | 4 |
| 39,850 | 48,800 | 44,325 | 3 | 0,050 | 7 |
| 48,800 | 57,750 | 53,275 | 16 | 0,267 | 23 |
| 57,750 | 66,700 | 62,225 | 21 | 0,350 | 44 |
| 66,700 | 75,650 | 71,175 | 12 | 0,200 | 56 |
| 75,650 | 84,600 | 80,125 | 2 | 0,033 | 58 |
| 84,600 | 93,550 | 89,075 | 2 | 0,033 | 60 |
| Контроль | 60 | 1,00 | | ||
-
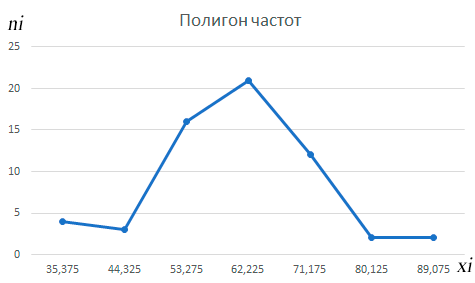
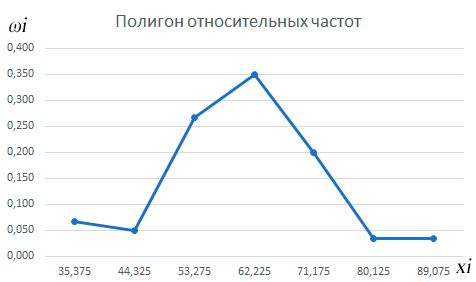
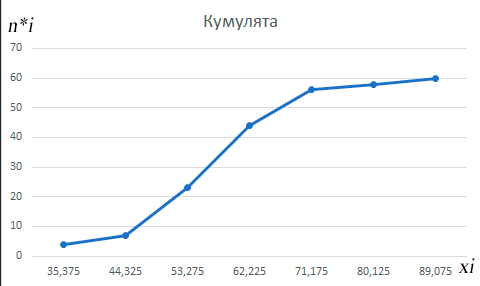
Начертить полигоны частот и относительных частот, кумуляту (по ряду 2) и гистограммы частот и относительных частот (по ряду 1).
Полигон частот строится в декартовой прямоугольной системе координат по точкам (хi ;ni), полигон относительных частот – по точкам (хi ;ωi), кумулята – по точкам (хi ; * i n ).
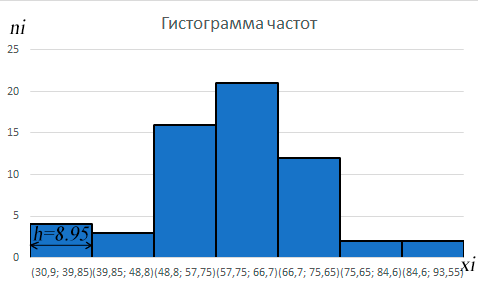
Фигура, состоящая из последовательности примыкающих друг к другу прямоугольников, называется гистограммой. Ширина этих прямоугольников равна ширине h интервалов группировки и откладывается по оси абсцисс, высота измеряется по оси ординат и пропорциональна частоте i n или относительной частоте i .
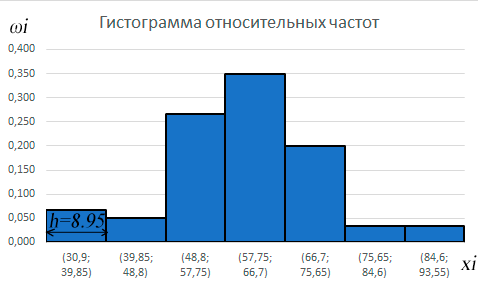
-
Записать аналитически и построить графически статистическую функцию распределения (по ряду 2).
Статистическая (эмпирическая) функция, F * (х) – это функция, которая для каждого значения аргумента равна относительной частоте попадания опытных данных в область, лежащую слева от аргумента

График статистической функции распределения F*(x) представляет собой ступенчатую фигуру со скачками в точках, определяемых элементами выборки. Технология построения статистической функции распределения F*(x) состоит в суммировании относительных частот для всех опытных значений, лежащих слева от аргумента. Другими словами, для получения значений статистической функции распределения полученные накопленные частоты делим на объем выборки.
При построении графика значения эмпирической функции распределения относят обычно к верхней границе частичного интервала.
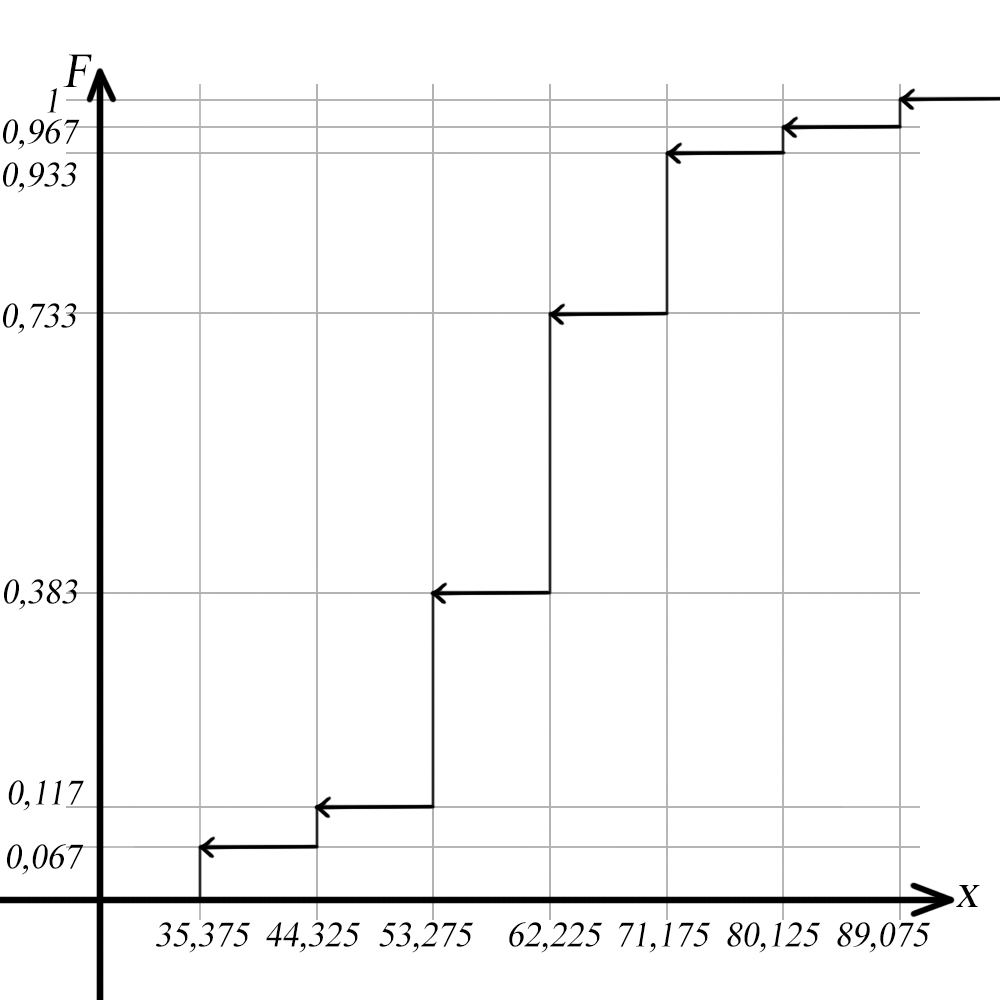
-
Найти выборочные средние: среднюю арифметическую, среднюю геометрическую, среднюю гармоническую; выборочную дисперсию, выборочное среднеквадратическое отклонение, коэффициенты вариации, асимметрии и эксцесс (по ряду 2) по общим формулам и с применением метода произведений.
Запишем формулы для поиска среднего выборочного, геометрического и гармонического и введем вспомогательную таблицу с промежуточными расчетами
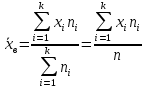
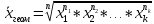
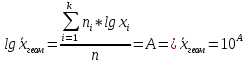
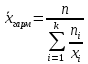
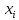 |  | 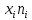 | 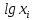 | 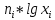 | 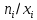 |
| 35,375 | 4 | 141,500 | 1,549 | 6,195 | 0,113 |
| 44,325 | 3 | 132,975 | 1,647 | 4,940 | 0,068 |
| 53,275 | 16 | 852,400 | 1,727 | 27,624 | 0,300 |
| 62,225 | 21 | 1306,725 | 1,794 | 37,673 | 0,337 |
| 71,175 | 12 | 854,100 | 1,852 | 22,228 | 0,169 |
| 80,125 | 2 | 160,250 | 1,904 | 3,808 | 0,025 |
| 89,075 | 2 | 178,150 | 1,950 | 3,900 | 0,022 |
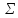 | 60 | 3626,100 | 12,422 | 106,367 | 1,035 |
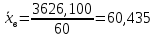
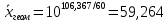
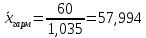
Между выборочной средней, средней геометрической и средней гармонической существует соотношение
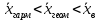
Неравенство выполняется
Вычисления характеристик статистических рядов рациональнее производить методом произведений. Так как значения равностоящие, перейдем к условным вариантам по формуле:
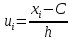
приняв
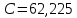 ,
, 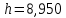
Для контроля вычислений воспользуемся тождествами:
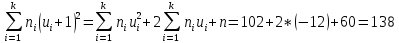
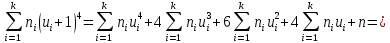
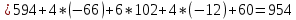
| Интервалы |  |  | 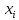 | 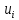 | 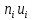 | 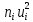 | 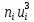 | 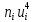 | 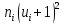 | 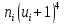 |
| (30,9; 39,85) | 4 | 4 | 35,375 | -3 | -12 | 36 | -108 | 324 | 16 | 64 |
| (39,85; 48,8) | 3 | 7 | 44,325 | -2 | -6 | 12 | -24 | 48 | 3 | 3 |
| (48,8; 57,75) | 16 | 23 | 53,275 | -1 | -16 | 16 | -16 | 16 | 0 | 0 |
| (57,75; 66,7) | 21 | 44 | 62,225 | 0 | 0 | 0 | 0 | 0 | 21 | 21 |
| (66,7; 75,65) | 12 | 56 | 71,175 | 1 | 12 | 12 | 12 | 12 | 48 | 192 |
| (75,65; 84,6) | 2 | 58 | 80,125 | 2 | 4 | 8 | 16 | 32 | 18 | 162 |
| (84,6; 93,55) | 2 | 60 | 89,075 | 3 | 6 | 18 | 54 | 162 | 32 | 512 |
 | 60 | | | 0 | -12 | 102 | -66 | 594 | 138 | 954 |
| | | | | | | | | Контроль | 138 | 954 |
