Вычислим условные моменты первого, второго, третьего и четвертого порядков по формуле









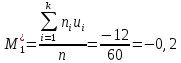
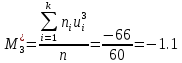
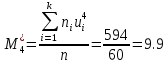
Согласно методу произведений, выборочная средняя и дисперсия определяются по формулам:





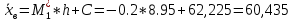
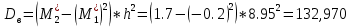
Значение выборочной средней, вычисленной по общей формуле и методу произведений, совпадает. Выборочное среднеквадратическое отклонение находится как корень квадратный из выборочной дисперсии:



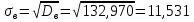
Коэффициент вариации определяется по формуле:



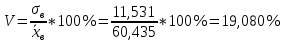
Центральные моменты, которые связаны с условными следующими соотношениями













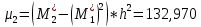
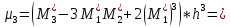
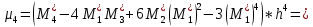
Характеристики формы распределения: коэффициент асимметрии и эксцесс, определяются по формулам









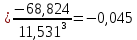
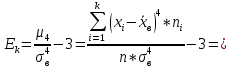
Отрицательное значение коэффициента асимметрии указывает на левостороннюю асимметрию кривой распределения, т.е. левая часть кривой длиннее правой и вершина кривой сдвинута влево. А положительное значение эксцесса говорит о том, что кривая распределения по сравнению с нормальной, менее крутая и имеет более острую вершину. Что

---

видно по графикам

6. 
   Определить моду и медиану графически и аналитически (по рядам 1 и 2).
   

Мода (модальное значение 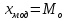) - наиболее часто встречающееся в статистической совокупности значение признака. Для дискретного вариационного ряда мода соответствует варианте с максимальной частотой. При определении моды обычно применяют следующие соглашения:

а) если все значения вариационного ряда имеют одинаковую частоту, то говорят, что этот вариационный ряд не имеет моды;

б) если две соседних варианты имеют одинаковую доминирующую частоту, что мода вычисляется как среднее арифметическое этих вариант

в) если две не соседних варианты имеют одинаковую доминирующую частоту, то такой вариационный ряд называется бимодальным (т.е. имеет две моды).

В нашем случае модальным интервалом является

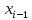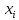57,750__66,700__62,225__21'>57,750	66,700	62,225	21

Также рядом с рядом стоящими

Модальность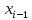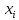
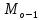	48,800	57,750	53,275	16
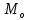	57,750	66,700	62,225	21
	66,700	75,650	71,175	12

---

В случае интервального вариационного ряда с равными интервалами модальный интервал (интервал, содержащий моду) определяется по наибольшей частоте. Вычисление моды производится по следующей формуле:





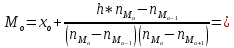
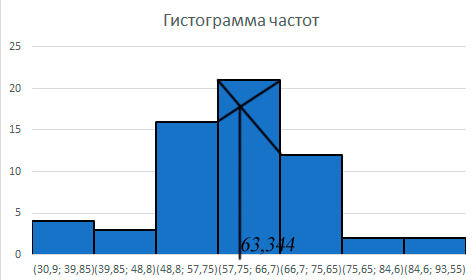
Для графического определения моды используют 3 соседних столбца гистограммы (самый высокий и 2 прилегающих к нему). Затем правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось абсцисс



В нашем примере медианным является следующий интервал ( ):

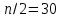Медианность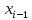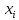
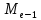	48,800	57,750	53,275	16	23
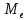	57,750	66,700	62,225	21	44

При вычислении медианы интервального вариационного ряда, сначала находят медианный интервал (интервал, содержащий медиану, в 10 котором содержится накопленная частота, превышающая половину объема выборки). Расчет медианы производится по формуле:

---

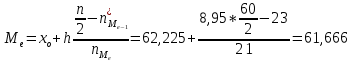
Медиана может быть определена графически по кумуляте. Для этого последнюю ординату, равную сумме всех частот, т.е. объему выборки n, делят пополам. Из полученной точки восстанавливают перпендикуляр до пересечения с кумулятой. Абсцисса точки пересечения и дает значение медианы

7. 
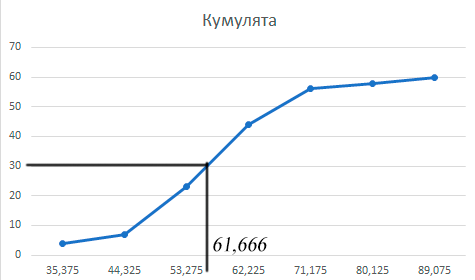
   На основе анализа гистограммы и статистической функции распределения оценить близость эмпирического распределения к нормальному закону, проверить гипотезу о том, что случайная величина Х имеет нормальный закон распределения по критерию Пирсона ( ).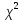
   

Рассчитаем 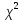для нашей выборки и сравним его с , но для этого вычислим ряд параметров и занесем все вычисления в таблицу

Для того, чтобы проверить согласуются ли данные выборки с нулевой гипотезой – гипотезой о нормальном распределении генеральной совокупности, поступают по следующему правилу:

1) выдвигают нулевую гипотезу о нормальном законе распределения случайной величины X и находят несмещенные оценки его параметров;


2) определяют теоретические частоты mi, соответствующие опытным частотам, если среди опытных частот имеются малочисленные, то их необходимо объединить с соседними

Перейдем к новым переменным по формуле:



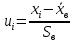
Найдем значения функций Лапласа от полученных переменных, используя статистические таблицы, причем полагают наименьшее значение ???????? = −∞, а наибольшее .

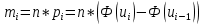
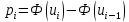
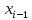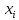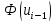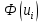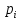30,900	39,850	-2,540	30,900	-0,50000	-0,46164	0,038
39,850	48,800	-1,770	39,850	-0,46164	-0,34134	0,120
48,800	57,750	-1,001	48,800	-0,34134	0,02392	0,365
57,750	66,700	-0,231	57,750	0,02392	0,09095	0,067
66,700	75,650	0,539	66,700	0,09095	0,22240	0,131
75,650	84,600	1,308	75,650	0,22240	0,48077	0,258
84,600	93,550	2,078	84,600	0,48077	0,50000	0,019
						1

---

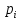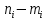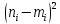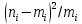0,038	2,302	1,000	3,000	9,000	9,000
0,120	7,218	7,000	-4,000	16,000	2,286
0,365	21,916	22,000	-6,000	36,000	1,636
0,067	4,022	4,000	17,000	289,000	72,250
0,131	7,887	8,000	4,000	16,000	2,000
0,258	15,502	16,000	-14,000	196,000	12,250
0,019	1,154	1,000	1,000	1,000	1,000
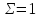	60	60			100,422

3) по формуле вычисляют статистику критерия;

---

Смотрите также файлы

• Конкурс Храбрый из храбрых.docx

• Вид работы Курсовая работа Название дисциплины Экономика организации (спо, курс 2) Тема Адаптация предприятия к рынку Фамилия студента Маликова Имя студента.doc

• лФараби атындаы аза лтты Университеті Сж таырыбы.docx

• Самостоятельная работа по теме 3 Уголовнопроцессуальное право Задание 1.docx

• Изучите описания характеристик групп задач трудового воспитания и выберите из выпадающего списка наименования, соответствующие данным описаниям. Заполните ими избранные ячейки таблицы.docx