МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«Тольяттинский государственный университет»
Тольятинский государственный университет

(наименование института полностью)

Росдистант

(Наименование учебного структурного подразделения)

08.03.01 Строительство

(код и наименование направления подготовки / специальности)

Промышленное и гражданское строительство

(направленность (профиль) / специализация)

Практическое задание №1
по учебному курсу «Механика жидкости и газа »

^{(наименование учебного курса)}
Вариант 09 (при наличии)

Обучающегося
	(И.О. Фамилия)
Группа
Преподаватель
	(И.О. Фамилия)

Тольятти 2023
Задание 1

Расчет простейшего эжектора

Провести расчет простейшего эжектора, состоящего из канала А и цилиндрического насадка В. Схема эжектора представлена на рисунке 1.

---

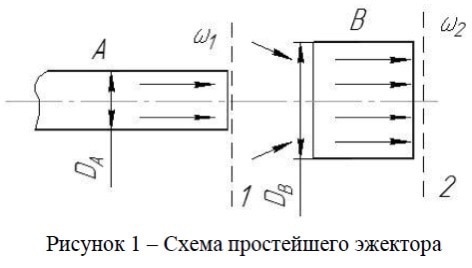
Определить скорость 2 и массовый расход газа на выходе из эжектора (сечение 2).

Дано:

Температура окружающей жидкости и жидкости в канале А: 25 оС

Давление окружающей среды: 0,1 МПа

Рабочее тело (жидкость): вода

Плотность жидкости: 1000 кг/м3

При расчете принимаются следующие допущения:

– силами трения о стенки эжектора пренебречь;

– вследствие малых скоростей жидкости считать плотность жидкости величиной постоянной;

– скорость жидкости в пространстве вокруг эжектора равна 0 м/с.

DA=20 мм, DВ=49 мм, w1 = 3 м/с.
Решение:

Построим контрольную поверхность из сечений 1 и 2, проходящих нормально к потоку по срезу канала А, смесительной камеры В и боковых поверхностей, направленных параллельно потоку. На всей полученной контрольной поверхности примерно одно и то же давление, равное давлению окружающей среды, т. е. главный вектор сил давления равен нулю.

Пренебрегая силами трения, то сумма проекций на ось трубы всех сил в пределах контрольной поверхности 1–2 равна нулю, следовательно, количество движения не меняется.

Изменение количества движения у активной струи на участке 1–2 равно:

G1(1 - 2).

Количество движения жидкости, подсосанной из окружающего пространства:

(G1 - G2)(2 - 0).

Суммарное изменение количества движения:

G22 - G11 = 0

где G1 и G2 – секундный массовый расход жидкости, кг/с;

1 и 2 – значения скорости истечения из канала А и смесительной камеры В соответственно, м/с.

Из уравнения 1.1 следует:

G2/ G 1= 1/2.
С другой стороны, отношение расходов жидкости можно записать как:



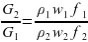
где  – плотность; f – площадь сечения.

Сравнивая последние два выражения, приходим к следующей

расчетной формуле:

---

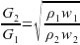
В нашем случае плотность жидкости в активной струе и окружающем

пространстве одинакова, следовательно, отношение массовых расчетов

жидкости равно отношению диаметров смесительной трубы и сопла:



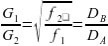
Подставляя значения диаметров, найдем отношение расходов:
G1/G2=49/20=2.45
Далее определим скорость жидкости на выходе из эжектора:


W2=3/2.45=1.224м/с
И наконец, определим расход жидкости на выходе:
G1=(w 2−w1 )= (2.45−3 )=1,776
G2=2.45∙1,776=4,351

---

Смотрите также файлы

• Тестовые задания Тест по разделу 1 Общие положения по.docx

• теория и методика обучения математике в профильной школе. задания к теме 5.docx

• Допущено Министерством образования Российской Федерации в качестве учебного пособия для студентов высших учебных заведений Москва оникс 2006 pressi ( herson ).pdf

• Одним из наиболее ярких проявлений эпохи переворотов на высшем уровне государственной власти стало уменьшение роли Сената.odt

• Методология и методы научного исследования. задание 1.docx