Файл: 1. в фирме 15 работников, 10 из них имеют высшее образование.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.03.2024
Просмотров: 38
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1. В фирме 15 работников, 10 из них имеют высшее образование.
а) Наугад выбирают одного работника. Найти вероятность того, что он не имеет высшее образование.
- m – количество благоприятных исходов (количество работников без высшего образования)
- n – общее число исходов (количество работников)
- используем классическое определение вероятности для нахождения итоговой вероятности:
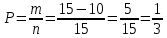
б) Наугад выбирают двух работников. Найти вероятность того, что они оба имеют высшее образование.
- найдём вероятность того, что выбрали первого работника, имеющего высшее образование:
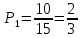
- найдём вероятность того, что выбрали второго работника, имеющего высшее образование:
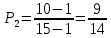
- используя правило умножения вероятностей, найдём итоговую вероятность:
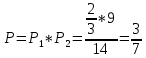
2. На пяти карточках написаны по одной из цифр: 1, 2, 3, 4, 5. Три из них произвольно вынимаются и укладываются на стол в порядке появления. Какая вероятность, что полученное число окажется меньше 400?
- m – количество благоприятных исходов (числа, меньшие чем 400; в нашей задаче данное число должно начинаться с 1, 2 или 3)
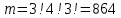
- n – общее число исходов
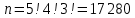
- используем классическое определение вероятности для нахождения итоговой вероятности:
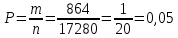
3. Студент может получить зачёт по английскому языку с вероятностью 0,8, а по математике — с вероятностью 0,6. Найти вероятность того, что:
а) будет получен только один зачёт;
- введём обозначения, которые будем применять при решении пунктов а) и б):
p1 – вероятность получения зачёта по английскому языку = 0,8;
q1 – вероятность неполучения зачёта по английскому языку = 1-0,8 = 0,2;
p2 – вероятность получения зачёта по математике = 0,6;
q2 – вероятность неполучения зачёта по математике = 1-0,6 = 0,4;
- «получен только один зачёт» = «есть зачёт по английскому языку и нет зачёта по математике, либо наоборот – есть зачёт по математике и нет зачёта по английскому»
- используя правило умножения и сложения вероятностей, находим итоговую вероятность:
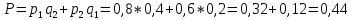
6) будет получен хотя бы один зачёт
Первый способ нахождения:
- «получен хотя бы один зачёт» = «есть зачёт по английскому языку и нет зачёта по математике, либо есть зачёт по математике и нет зачёта по английскому, либо есть оба зачёта»
- используя правило умножения и сложения вероятностей, находим итоговую вероятность:
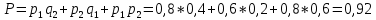
Второй способ нахождения:
- найдём вероятность события, при котором студент не получает зачёт сразу по двум предметам (
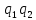), а затем вычтем данную вероятность из единицы: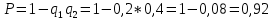 
4. В городе 5 коммерческих банка. У каждого риск банкротства в течение года составляет 10%. Найти вероятность того, что 2 из них обанкротятся в течение года.
- воспользуемся формулой Бернулли:
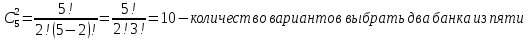
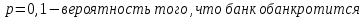
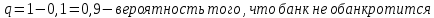
- итоговая вероятность:
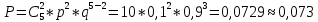
5. Из букв разрезной азбуки, составляющих слово «мороз», наугад берутся 3 буквы. Случайная величина Х — число взятых гласных букв. Найти ряд распределения, математическое ожидание М(
X) и дисперсию D(Х).
| Xi | 0 | 1 | 2 |
| Pi | - | - | - |
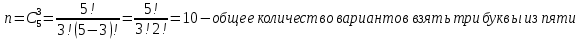
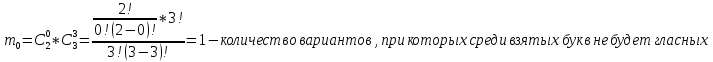
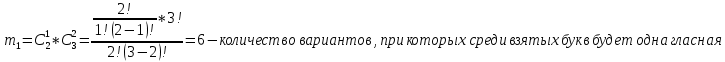
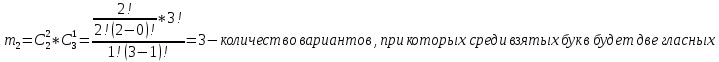
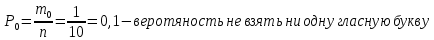
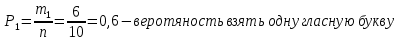
- получаем следующий ряд распределения:
| Xi | 0 | 1 | 2 |
| Pi | 0,1 | 0,6 | 0,3 |
- найдём математическое ожидание:
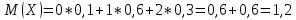
- найдём дисперсию:
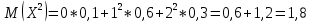
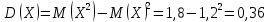
6. Выборочные данные представлены статистическим рядом:
| Xi | -1 | 2 | 5 | 8 |
| Ni | 8 | 10 | 20 | 12 |
а) Найти выборочное среднее
- воспользуемся следующей формулой:
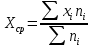
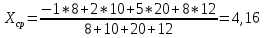
б) Найти исправленную выборочную дисперсию s2
- воспользуемся следующей формулой:
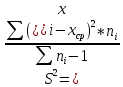
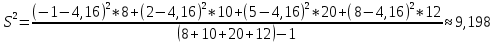
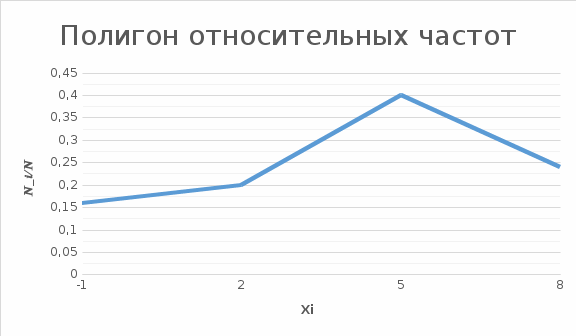
в) Построить полигон относительных частот.
- дополним нашу исходную таблицу:
| Xi | -1 | 2 | 5 | 8 |
| Ni | 8 | 10 | 20 | 12 |
 |  |  |  |  |
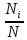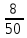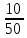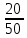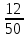или:
| Xi | -1 | 2 | 5 | 8 |
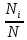 | 0,16 | 0,2 | 0,4 | 0,24 |
